LA INGENIERIA, LAS CIENCIAS DURAS Y SU VISION DEL MUNDO

Todo profesional profesa, - es decir cree en -, un esquema interno que utiliza como guía para operar en su profesión. Los médicos tienen una imagen del cuerpo, los arquitectos tienen una imagen de cómo deben ser y funcionar los edificios y las ciudades, los economistas y administradores tienen un esquema mental de como interactúan los factores económicos, y así siguiendo. Tener este esquema interno es una condición necesaria de lo que llamamos "saber".

Estos esquemas internos son más o menos rígidos en función de la estrictez de las disciplinas que forman parte de ellos. Cuando la ciencia acepta un esquema enraizado en las matemáticas, con definiciones precisas y causalidades estrictas, hablamos de ciencias duras. Por el contrario cuando es difícil extraer de la realidad conceptos precisos y relacionarlos con rigor, hablamos de ciencias blandas. En general, las disciplinas técnicas requieren ciencias duras; las humanistas, ciencias blandas; el resto queda en el medio. Las artes no clasifican -felizmente - como ciencia.

Este esquema interno que cada profesional lleva incorporado, es una especie de "soft" que opera no solo en su actividad profesional sino en su vida diaria. Las mentadas deformaciones profesionales son el resultado de la dificultad de restringir su aplicación tan solo al campo laboral para el que ha sido previsto. Sin darse cuenta, el profesional aplica estos criterios también a su vida social, familiar, etc.

En una primera aproximación, podemos decir que la ingeniería trata acerca de las reglas que permiten prever el comportamiento de la materia inerte, y de las técnicas aplicables para modificar la misma en aras de un mayor confort de la sociedad en que cada uno vive. Si bien algunas de sus ramas toman en cuenta al hombre, lo consideran tan solo un paso intermedio del proceso hacia el objetivo final: crear un "ingenio" que sea "útil".

Una parte importante de estas reglas se expresan en relaciones matemáticas. Las ciencias en las que se apoya la ingeniería serán en consecuencia ciencias duras en las que no hay lugar para "opiniones": Una expresión será cierta o falsa según se ciña o no a reglas explícitas que, validadas por comprobaciones experimentales anteriores y ordenadas según la lógica cartesiana, son aceptadas como reglas del arte.

El hecho de que el área en el que el ingeniero opera acepte leyes lógicas y deterministas, marca profundamente su versión genérica de la realidad, a la que trata de encuadrar en leyes de las mismas características. Esto es consecuencia no tanto de su experiencia en el ejercicio de la profesión, sino de sus vivencias en el curso de su formación universitaria..

Los primeros años de su formación están consagrados al: análisis matemático, a diversas geometrias, a la física y química de laboratorio, sin que nadie le explique la relación que estas disciplinas tienen con la realidad, ni mucho menos las simplificaciones que han sido necesarias para poder encuadrar la realidad en esas reglas. Es así que quien se apasione por el estudio de estas disciplinas, puede llegar a creer que las construcciones simbólicas son la realidad, o dicho de otra manera, que la realidad "obedece" a estas estructuras simbólicas que parecerían contenerla. Y aún los indiferentes, luego de pasar largas horas analizando funciones de significado ignoto sin llegar a entender aún muy bien de qué se trata, aceptarán con fe que lo que estudian es una clave que desentraña la realidad.

Y este mensaje implícito no es demitificado. Por el contrario en los últimos años de su "carrera", el aprendiz comprueba que sus reglas permiten modelar la materia transformándola en las maravillas tecnológicas que usamos todos los días. Siente que sabe y puede, y olvida, a menudo, que no todo puede ser así pensado..

¿Qué consecuencias tiene en la vida de un ingeniero esta formación lógico matemática que ha incorporado a su acervo cultural?

¿Cómo se comunica, por ejemplo, con un abogado que considera que un mismo hecho puede ser interpretado de dos maneras totalmente distintas según "la mitad de la biblioteca que tome en cuenta" mientras que él cree que "las cosas son como son", que una dada causa debe producir siempre los mismos efectos?

-¿Cómo se maneja al considerar, solo frente a un espejo, la vieja pregunta de la vida y su sentido, cuando por una parte "cree" que "en realidad" la variable tiempo es reversible (aunque lamentablemente no para él) y que el destino está escrito, mientras que por otra parte, tiene una clara vivencia de poder elegir en su "menú" su próxima acción sin que ningún control extraño lo comande?

Son temas privados que no tienen respuesta cierta ni utilidad concreta y que por lo tanto obviaré. Insistiré por el contrario en la pregunta de qué es lo que implica la imbricación de la causalidad en la cultura del ingeniero. Una eventual respuesta quizá pueda ayudar en el manejo de las cuestiones anteriores.

Recordemos que en el primer curso de análisis nos enseñaron series y progresiones en las que cada término se definía en función del término anterior. El problema básico era encontrar la expresión genérica del enésimo término, sin transitar por los términos intermedios. Nadie señaló que cuando la expresión era cuadrática, raramente existía una expresión genérica para el enésimo término. Eran casos que por no tener solución, no eran tema de estudio.

Más tarde estudiamos cómo, a partir de la velocidad y masa de un cuerpo ubicado en un dado campo de fuerza, se puede calcular su trayectoria, tanto recorrida como a recorrer. Se trataba tan solo de aplicar ecuaciones diferenciales que, siendo integrables, podían ser resueltas. Nadie mencionó que los sistemas no canónicos generan términos que imposibilitan la resolución, lo que nos permitió suponer que las trayectorias de los planetas y sus lunas transitaban órbitas no solo permanentes sino idénticas.. Sin embargo ya a fines del siglo pasado Poincaré había demostrado que las ecuaciones de las trayectorias de tres o más cuerpos interactuando generaban resonancias que hacían que el sistema no pudiera ser resuelto. Las órbitas sólo pueden ser calculadas por iteraciones, cambian con la posición relativa de los cuerpos, y son potencialmente inestables.

Es decir que considerábamos expresiones matemáticas que podían ser resueltas, las que a su vez correspondían a comportamientos deterministas de la naturaleza, y descartábamos aquellas que "aún no habían sido resueltas". Se sobreentendía que las situaciones que estas últimas reflejaban respondían también a un determinismo que no podía ser develado por una insuficiencia en la capacidad de medición y/o de cálculo, pero no por una causa intrínseca al cálculo en sí. Existirían ecuaciones que, aunque aún no escritas, permitirían en un futuro utópico conocer la historia del universo tanto pasada como futura, y proyectarla como en un cine, tanto hacia adelante como hacia atrás.

Y por extensión también sobreentendíamos que desarrollándose la vida en la materia, - materia autoorganizada pero materia al fin -, la causalidad y su supuestamente implícito determinismo también operaban en ese campo. Las ciencias blandas eran "ciencias en estado de desarrollo", que con el tiempo descubrirían sus leyes duras y las matemáticas correspondientes. En una última instancia, el hombre diseñaría una red simbólica final que se superpondría exactamente con la realidad.

Esta versión decimonónica de la ciencia, que ya comenzó a resquebrajarse a principios de siglo con las paradojas de la mecánica cuántica y el teorema de Godel, era sin embargo la que se respiraba en nuestra facultad de los años cincuenta. En particular era aceptado el hecho que en física, causalidad y determinismo eran equivalentes, en tanto y en cuanto no existía ningún experimento que pusiera en evidencia una contradicción en la supuesta identidad.

Hoy no existe más esa certeza. La capacidad de las computadoras de repetir un dado cálculo en tiempo breve y a bajo costo, ha permitido la iteración de aquellas series y expresiones que no aceptaban soluciones directas.

Esto corrió las fronteras de cálculo y produjo una ruptura epistemológica que abrió el campo a las teorías del caos, la complejidad y los fractales.

A pesar de ello aún hoy se discute si la aparición de valores imprevisibles en el cálculo de algunas series, debe ser simplemente atribuida a una falta de capacidad de la computadora, o si por el contrario no es lógicamente posible construir una computadora capaz de calcular el valor "cierto" de sus términos. O dicho de otra manera: ¿la imposibilidad de alcanzar valores no sólo previsibles, sino únicos y ciertos para los términos de algunas series es consecuencia de una deficiencia física de la máquina o es inherente a la esencia misma del cálculo y los elementos que en él intervienen?

Una perspectiva rápida de la situación actual se alcanza con un simple experimento matemático.

Si consideramos la serie X_t+1 = Ç.X_t.(1-X_t) y la iteramos en nuestra computadora para distintos valores del coeficiente Ç, - iniciando la iteración con cualquier valor de X_o comprendido entre 0 y 1 para que los términos sean positivos -,.observaremos:

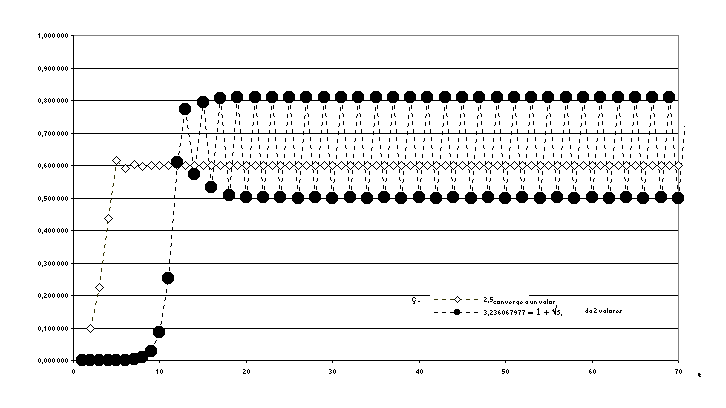
• a medida que aumentamos Ç a partir de 0, la serie converge cada vez más lentamente en valores que crecen en el mismo sentido que Ç. Así por ejemplo, para, Ç=2,5, la serie termina estabilizándose en un valor de 2,6. (Fig.1)

• cuando el valor de Ç supera un valor de aproximadamente 3, la serie en lugar de estabilizarse en un único valor comienza a rebotar indefinidamente entre 2 valores. Así por ejemplo para Ç=1+Ö5 la serie rebota entre 0,80902 y 0,5. Este es el primer caso de un ciclo límite, pues la serie rebota solamente entre 2 valores. (Fig.1)

• si continuamos aumentando el valor de Ç, la serie comienza a oscilar primero entre 4 valores, luego entre 8, 16, 32, etc., duplicando vez tras vez la cantidad de valores entre los que oscila. Así por ejemplo para Ç=3,55 los rebotes se producen entre 8 valores que se repiten siempre en el mismo orden. (Fig.2)

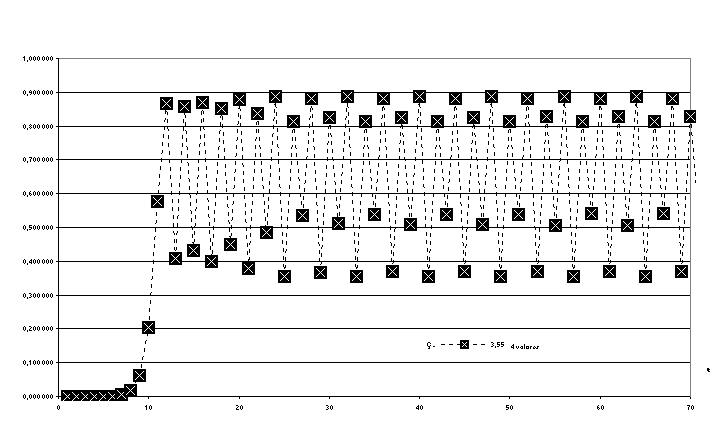
Figura 2

• la duplicación de valores que se repiten en forma sucesiva se mantiene hasta Ç=3,5699, pudiéndose identificar 2048 valores entre los que rebota la serie en el mismo orden. (Fig.3)

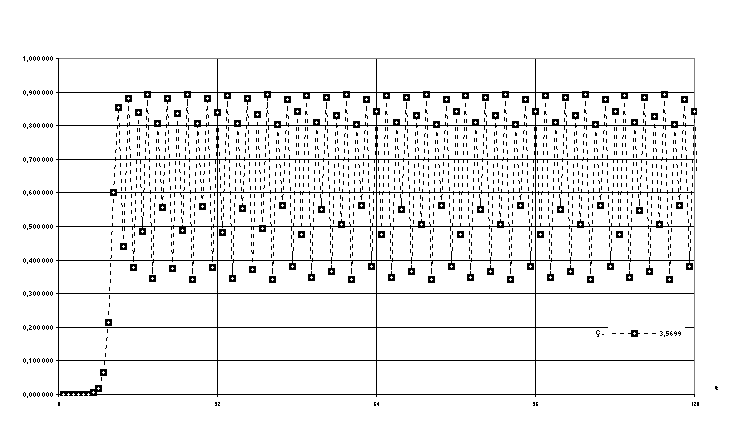
Figura 3

• luego de Ç=3,57 la duplicación se interrumpe, y se obtienen valores que se repiten solo ocasionalmente y sin ningún orden, hasta que para Ç=4, los términos no se repiten nunca y las cifras aparentan ser totalmente aleatorias sin ninguna relación causal entre ellas. (Fig.4)

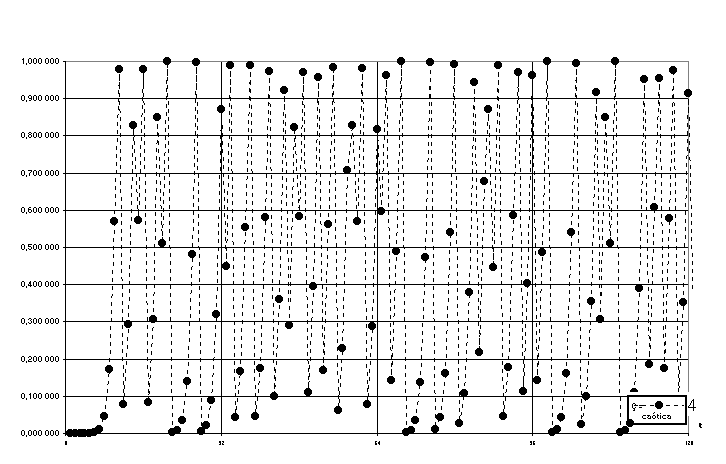
Figura 4

La expresión que hemos comentado es denominada "logistic map", habitualmente utilizada como introducción a la teoría del caos. El primer punto clave radica en que cuando entra en la "zona caótica" (Ç>3,5699), los términos toman valores cada vez más caprichosos hasta lucir como totalmente aleatorios a pesar de la situación de estricta causalidad imperante.

Ahora bien. ¿Qué tiene que ver el comportamiento detallado con la relación entre causalidad y determinismo? El hecho de que la causalidad pueda asumir formas aparentemente caóticas es ciertamente interesante; y tiene como contrapartida que permite suponer que algunos fenómenos en apariencia aleatorios, puedan responder a leyes causales relativamente sencillas. Pero esto no agrega nada a nuestra cuestión. Si bien la serie estudiada no tiene, como tantas otras, una expresión para el término genérico, todos y cada uno de sus términos pueden ser calculados paso por paso, lo que hace que sus valores estén causalmente definidos y unívocamente determinados.

En busca de más luz demos otra vuelta de tuerca al experimento. Comparemos cómo evoluciona la serie cuando para un dado valor de Ç adoptamos distintos valores iniciales de Xo.

Observaremos que para valores de Ç<3,5699 , la serie se estabiliza siempre en los mismos valores, sean estos 1, 2, 4, 8, ...., 2048, independientemente del valor de Xo con que hayamos iniciado la iteración. Por el contrario en la zona caótica no se produce ningún tipo de convergencia por lo que tampoco hay coincidencia alguna entre los términos de las iteraciones, que evolucionan cada uno a su manera de acuerdo al valor Xo con el que se iniciaron.

Aumentemos ahora la precisión del valor Xo con el que iniciamos sucesivas iteraciones, manteniendo constante un valor de Ç=4. Para ello:

Vemos que nos encontramos ante una nueva manifestación caótica, que difiere substancialmente de la anterior. Ahora, lo caótico del sistema no reside apenas en el hecho que sus términos se suceden en forma aparentemente aleatoria, sino en el hecho que el valor de un término cualquiera asume valores totalmente diferentes al aumentarse la definición del término con el que se inicia la iteración.

Repitamos ahora la pregunta anterior. ¿Compromete esto la supuesta identidad entre causalidad y determinismo? La respuesta es sí, dado que a pesar de la causalidad imperante, los valores de los términos tomarán valores radicalmente diferentes que aparecerán sin ton ni son a medida que aumente la cantidad de decimales (y por ende la precisión) con que fijo las condiciones iniciales. Es decir que para cada término de la serie tendré infinitos valores distintos que corresponderán a los decimales que haya elegido tomar entre los infinitos disponibles. (Infinitos valores entre los que no podré privilegiar a ninguno, dado que cada uno corresponde a una cantidad de decimales - y a una precisión - adoptada arbitrariamente). Por lo que el valor de cada término es indeterminado, a pesar de que cada uno de ello ha sido calculado de acuerdo a la misma ley de causalidad.

Lo que antecede ayuda quizás a interpretar el repetido dicho que el aleteo de una mariposa en el Japón perturbará el clima en la costa oeste americana, escuchado hasta en boca de los científicos de Jurasic Park. Se trata de que la mínima influencia del aletear de una mariposa se reflejará aunque más no sea en el centésimo, milésimo o millonésimo decimal del valor inicial de cálculo de la evolución del clima en el Pacífico, modificación que, aunque parezca despreciable, transformará - quizás - una suave brisa californiana en un huracán.

Esta característica de impredictibilidad más allá de un horizonte más o menos cercano se presenta en todos los fenómenos que pueden ser interpretados por expresiones cuyo comportamiento es caótico. Lo interesante es observar que la limitación última reside no en el desconocimiento de las leyes que rigen el fenómeno, ni tampoco en las capacidades físicas de medición de parámetros, sino en las características matemáticas de las leyes que entran en juego. En particular, cualquier modificación en las condiciones iniciales por más pequeña que sea, causará en las condiciones finales modificaciones no sólo grandes sino también impredecibles.

Esta situación se presenta no solo en meteorología sino también en economía, biología, ecología y hasta en áreas de química y mecánica. En todas estas disciplinas conviven la causalidad - cuya presencia debemos necesariamente reconocer como condición para mantenernos cuerdos -, con la indeterminación - que nos permite sentirnos libres de optar en un mundo en el que no está todo escrito.

Es un panorama menos firme que el que recibimos en su momento, pero más alegre. Que quizá socave nuestra fe en las ciencias duras, pero también facilite nuestra aceptación de las contradicciones tanto propias como ajenas.

Back to index - Volver al índice