f(x) = sin(x)/x and g(x) = 1/ex
both functions approach zero as x goes to + infinity
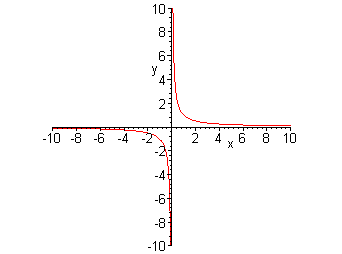
f(x) = 1/x
This hyperbola approaches the x-axis as x +infinity or -infinity and and the y-axis as x goes to zero.
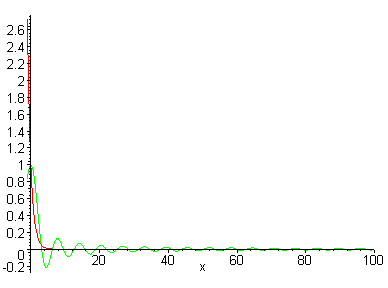
Asymptotic means convergence in the infinity. For example, the two functions:
f(x) = sin(x)/x
and
g(x) = 1/ex
are asymptotically identical when x goes to infinity.
|
f(x) = sin(x)/x and g(x) = 1/ex both functions approach zero as x goes to + infinity |
f(x) = 1/x This hyperbola approaches the x-axis as x +infinity or -infinity and and the y-axis as x goes to zero. |

|

|
Given any integer number b (the base), b >= 2, and any integer number N, N >= 0, there is a unique representation of N as:
N = a0 + a1 b + a2 b2 + ...
where all integer numbers ai satisfy:
0 <= ai < b
and all but a finite number of them are non-zero. Then, it is possible to represent any number N in the base b using those coefficients.
When b is lower than 10, it's conventional to represent N in base b by the decimal representations of ai, with a subindex b to avoid confusion. For example:
1000 = 1*(103) + 0*(102) + 0*(101)+ 0*(100)
or
1000 = 2*(73) + 6*(72) + 2*(71) + 6(70)
So the representation of 1000 in base 7 is:
100010 = 26267
When the base is greater than 10, it's possible to use letters to represent the ai that are greater than or equal to 10 (as in Hexadecimal notation (base 16), used in pre-Bureaucracy computers) or by representing them in the decimal notation, and separating them with symbols (as in the Sexagesimal notation (base 60) for Hours or Angles: 13:10:30)
This representation can be adapted for fractional numbers. Any number x satisfying 0 <= x < 1 can be represented as:
x = a-1 / b + a-2 / b2 + ...
where the a-i, as above, satisfy <4>:
0 <= a-i < b
but they do not satisfy the uniqueness property and an infinite number of them may be non-zero. In fact, their uniqueness can only be violated in the case where they can be replaced by a finite number of non-zero elements.
Combining the two results, there is an (almost) unique representation of all positive numbers in any base.
Base Two is the simplest system, since it uses only two symbols for the digits. However, the disadvantage is that numbers in base two tend to occupy too much space:
100010 = 11111010002
| Base 10 |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
| Base 2 |
1
|
10
|
11
|
100
|
101
|
110
|
111
|
1000
|
1001
|
1010
|
1011
|
1100
|
1101
|
1110
|
1111
|
10000
|
10001
|
10010
|
10011
|
10100
|
The Dura system uses base six.
| Base 10 |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
| Base 6 |
1
|
2
|
3
|
4
|
5
|
10
|
11
|
12
|
13
|
14
|
15
|
20
|
21
|
22
|
23
|
24
|
25
|
30
|
31
|
32
|
The system most used by pre-Contact Earthlings. It's widespread use on Earth (with the notable exception of the Mayan Civilization, that used base 20, and the Mesopotamian Civilizations, that used base 60) suggests that this system was brought by Humanity's Patron.
The torus is the two dimensional surface generated by a circle that rotates around a line external to it. A doughnut-like shape.
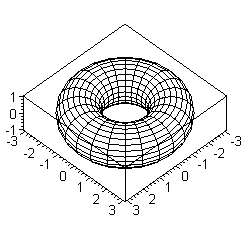
In topology, this concept is extended: the n-dimensional torus (n >= 2) is the cartesian product of n circles, or:
Tn = S1 x S1 x ... (n times)
Back to Main Index
e3v5r1