Kinematics of the Long Jump (Pictures)

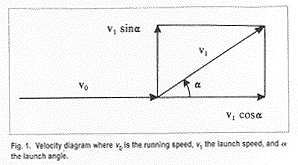
Fig.1. Velocity diagram where vo is the running speed, v1 the launch speed, and a the launch angle.

 

Fig. 2. Geometry of the long jump: a and b are distances of centers of gravity of jumper from takeoff and landing points, respectively; a is the launch angle and b the landing angle.

 

Table 1. 0ptimum launch angle for maximum range.

 

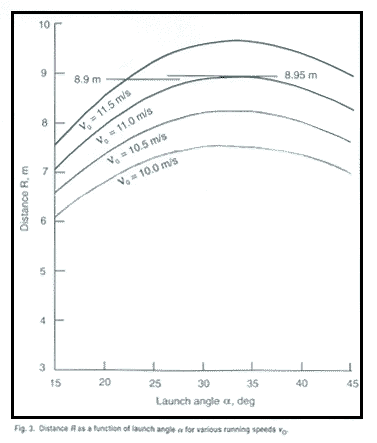
Fig. 3. Distance R as a function of launch angle a for various running speeds n o .

Kinematics of the Long Jump

        The long jump is one of the most natural events in track and field athletics. The jumper is allowed to run a 40-m runway at top speed and jump as far as possible from a takeoff board. It is an event in which the natural ability of the athlete plays a large role and technique is of secondary importance. The two most important factors in the long jump are speed and elevation. This is exemplified by the fact that two of the greatest long jumpers in history, Jesse Owens and Carl Lewis, were also the greatest sprinters of their times. Their jumping ability depended mainly on their raw speed. Other long-jumping greats such as Ralph Boston, Bob Beamon, and Mike Powell (the current world-record holder) depended more on elevation to compensate for lack of blazing speed. Ralph Boston,for example, made high jumps of 6 ft 9 in.

       What is the optimum launch angle for maximizing the long jump from akinematical point of view? It is well known that, in the absence of air-resistance, the optimum launch angle of a projectile for maximum range on a horizontal plane is 45°. However, this is not applicable to the long jump, where the jumper has to launch himself at the expense of a part of his translational kinetic energy before takeoff.

       We first calculate the optimum launch angle of a long jump in the horizontal plane neglecting air resistance. This would be the case if the jumper landed vertically so that his center of gravity remained at the same height at launch and landing.

       Let n o be the initial speed of the jumper before takeoff; n 1 the launch speed; and a the launch angle of the jumper (Fig. 1 ). The total energy, before takeoff is then E 0 = ½mn 0², which is of translational kinetic form. A fraction g of this energy is wasted as heat and sound. Another part, D E, is converted into the energy of vertical motion:
D E = ½mn 1²sin²a .The translational kinetic energy of the jumper after takeoff is
E 1 = ½mn 1 ². By the law of conservation of energy, we have : E1=E0-g E0-D E (1).Upon substituting values of the terms in Eq. (1) and simplifying, we obtain: v1 = [ (1 - g ) ¹/² / (1 + sin² a )¹/² ] n o (2)

        The range R of the projectile on a horizontal plane is obtained from elementary kinematics: R = n 1 ² sin2 a / g = A sen2 a / 1 + sin²a (3) where A = ( 1 -g ) n o ² / g     Differentiating Eq. (3) twice with respect to a and simplifying, we get : dR / da = [ 3 cos2 a -1 / (1 +sin²a )²] A (4), and d²R / da ² = [ 4 (3 sin4 a + 1 4 sin2 a ) / (cos2 a - 3 )³ ] A (5)

        Setting dR/da = 0, we obtain the optimum launch angle on a horizontal plane: a m = ¹/² cos-¹ (1/3) = 35.26°. By substituting this value of a in Eq. (5), we can confirm that this corresponds to a launch angle for maximum range. Notice that this angle is independent of n o or g .

        In reality, the jumper lands with his feet in front of his body to further the jumping distance (Fig 2). In this position, the center of gravity of the jumper is at a distance h below its level at takeoff and the distance b between the center of gravity and the feet is also shorter than that at takeoff, a (see Fig.2). If b is the angle of landing, then h = a – b sinb . In this situation, the distance of the long jump is given by:R= n 1 cosa / g [ n 1 sina + (n 1 ² sin²a +2 gh)¹/² ] + L (6), where L = b cosb , On substituting n 1 from eq. (2) we get : R = A [ sin2 a / 1 +sin²a {1 +[1 +B (1 + sin²a / sin²a )¹/²] } + L (7), with B = h/A.

        In principle, the landing angle b should be made as small as permissible, but it must also be numerically greater than the angle of descent so that the jumper does not land on his seat. Experience tells that this angle is about 45°. With reference to the definition of b , note that the angle betwwen the legs and the horizontal is considerably smaller. Treating L as a constant, we can find the launch angle for maximum range analytically. Differentiating Eq. (7) with respect to a , setting the derivative equal to zero and simplifying, we arrive at a transcendental equation: p( a ) = q( a ) (8), where p( a ) = 2 + 1 2 B + 2 ¹/² cosec a [1 + 3 + B - (B +1) cos2a ]¹/² (9) and q( a ) ={6 + 4 B + 3 2 ¹/² cosec a [1 + 3 B - (B +1) cos 2a ] ¹/² } cos2a (10).

        Equation (8) may be solved graphically or using numerical calculation. For a jumper of Carl Lewis's height (1.86 m or 6 ft 2 in ), a = 0.93m. Estimating b to be 0.6m and b = 45°, we get, approximately, h = 0.51m and L = 0.42m. Further, the analyses of McFarland and Tan suggest that y =1/10. Calculating both sides of Eq, (8) using incrementally increasing launch angles, we obtain the optimum launch angle for maximum range a(alfa)m. Table 1 displays the results for various initial speeds n o . It is evident that a m is now smaller than the earlier value of 35.26° for the horizontal plane. Also, a m increases slightly with n o . This is consistent with expectation since the angle of incline decreases with increasing n o and therefore increasing R.

        According to model calculations,11.5 m/s was the limiting speed of one of the fastest 100-m runs by Carl Lewis. Contrary to the much higher figures stated elsewhere in the literature, this is close to the fastest speed ever achieved by a human. Table I shows that with such a running speed, it is theoretically possible to long jump 9.69 m or 31 ft 9 in.Because that is over 2 ft longer than the current world record of 8.95 m or 29 ft 4¹/² in, this distance may be considered as the upper limit of long jumping at the present time. The table further indicates that in order to better the current world record, the jumper must have a running speed of at least 11 m/s. In a memorable jumping duel between Carl Lewis and Mike Powell, both jumpers flirted with the old world record of nearly 23 years standing held by Bob Beamon (8.90 m or 29 ft 2¹/² in) before Mike Powell actually achieved the current world mark. Lacking Lewis's blazing speed, Powell must have used a high launch angle to attain his record.

        lt was estimated that Jesse Owens used a launch angle of between 25° and 26° or considerably lower than the optimum launch angle of a(alfa)m derived here. However, this is not so surprising, considering the fact that Owens, like Lewis, was a speed jumper. Other long-jump notables such as Ralph Boston, Bob Beamon, Lynn Davies, and Arnie Robinson, all relied on elevation to attain their distances. Figure 3 shows the dependence of the distance R on the launch angle for various running speeds. It reaffirms the fact that the minimum running speed required to equal or better the present world mark is 11m/s. Figure 3 further illustrates that Carl Lewis, who had registered more 28-ft jumps than all other human beings combined, and who chased Beamon's elusive world mark unsuccessfully at sea level, could, in theory, have achieved his goal using a launch angle of as low as 22°.