FÓRMULAS QUE GERAM NÚMEROS PRIMOS
- Um livro -
[ Números primos | Fórmulas para primos | O livro]
[ O autor | Como comprar | Entre em contato ]
[ Bibliotecas onde consultar | INÍCIO ]
Um número natural é primo quando tem exatamente dois divisores positivos distintos. Assim, 1 não é primo, pois só tem um divisor positivo; 5 é primo pois tem dois divisores positivos distintos, a saber, 1 e 5; mas 10 não é primo pois tem quatro divisores positivos, a saber, 1, 2, 5 e 10.
Os dez primeiros números primos são 2, 3, 5, 7, 11, 13, 17, 19, 23 e 29.
Os números primos desafiam há muito tempo a engenhosidade e a imaginação do ser humano. Muitas questões interessantes podem ser levantadas, no que diz respeito à distribuição, reconhecimento e geração. Em particular, pode-se questionar a existência de uma fórmula para gerar a seqüência dos números primos, ou seja,
determinar uma função f, tal que dado um número natural não nulo n, f(n) seja o n-ésimo número primo
ou, ainda, em outra versão do problema, questionar a existência de uma fórmula para gerar números primos, ou seja,
determinar uma função f tal que dado um número natural não nulo n, f(n) seja um número primo.
Exemplo:
Escreverei a^b para significar a elevado a b. Pierre de Fermat (1601-1665) conjecturou que todos os números da forma F(n) = 2^(2^n)+1, onde n é um inteiro positivo, são primos. Por exemplo:
F(1) = 2^(2^1)+1 = 5 é primo;
F(2) = 2^(2^2)+1 = 17 é primo;
F(3) = 2^(2^3)+1 = 257 é primo;
F(4) = 2^(2^4)+1 = 65537 é primo.
Porém, em 1732, Leonhard Euler (1707-1783) mostrou que F(5) (um inteiro de 10 algarismos) é divisível por 641 e portanto não é primo.
Um resultado bem conhecido da álgebra afirma que não existe um polinômio, com coeficientes racionais, que produza somente números primos. Embora estabeleça uma limitação a geração de números primos, este resultado não exclui a existência de:
a) funções polinomiais em uma variável que gere números primos, mas não todos;
b) funções não polinomiais que gerem números primos, todos ou não;
e até mesmo
c) funções polinomiais em mais de uma variável que produzam números primos, todos ou não.
Embora muitos professores e estudantes de Matemática desconheçam este fato, existem funções com cada uma das características acima.
Exemplos:
a) Considere a função f(n) = n^2 - n + 41, com n um número natural.Já sabemos que esta fórmula não pode produzir todos os primos pois é um polinômio em uma variável com coeficientes inteiros. Mas o fato curioso é que para n = 1, 2, 3, ..., 40, f(n) é primo enquanto que para n = 41 tem-se f(n) = 1681 = 41^2 que não é primo;
b) Um exemplo do segundo tipo é a função dada em 1971 pelo matemático J.M. Gandhi,
que fornece o n-ésimo número primo em função dos n-1 primos
anteriores
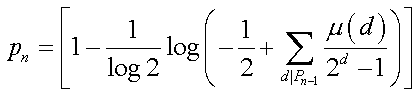
onde pn é o n-ésimo número primo e Pn-1 = p1p2...pn-1 é o produto dos primeiros n-1 primos. O símbolo d|m significa "d divide m" e portanto o somatório deve ser feito para todo divisor d de Pn-1.
c) Um exemplo do terceiro tipo é a fórmula pode ser encontrado num outro
website clicando aqui
O livro "Fórmulas que geram números primos"
O livro convida quem tem interesse em Matemática a conhecer um assunto pouco divulgado: fórmulas que geram números primos.
Este tema, embora fascinante, tem sido ignorado por muitos estudantes, professores e matemáticos.Apesar de diversas funções que geram números primos terem sido obtidas pelos estudiosos de Teoria dos Números, muitas pessoas interessadas em Matemática não refletem mais profundamente sobre o assunto,apenas porque nunca viram tais funções ou acreditam, erroneamente, que elas não existem.
Além de uma revisão histórica, o livro apresenta vários exemplos, com provas, de fórmulas que produzem infinitos números primos e apenas primos.
Um curso introdutório de Teoria dos Números e um de Análise Real - ambos a nível de graduação - são desejáveis como pré requisitos, muito embora o livro possa ser estudado com proveito por qualquer um que tenha conhecimentos Matemáticos equivalentes aos adquiridos no final do Ensino Médio.
Os conteúdos abordados são os seguintes: Teoria (Elementar) dos Números (congruências módulo n, divisibilidade, números binomiais, frações contínuas), Análise Real (sucessões, convergência, seqüências duplas), - cada capítulo é independente e pode ser lido sem prévio conhecimento dos outros:
1.
FÓRMULAS QUE GERAM NÚMEROS PRIMOS
Eric estudou Matemática na Universidade Federal Fluminense, em Niterói, de 1995 a 1998. Em 1991, conquistou o 2º prêmio na XIII Olimpíada Brasileira de Matemática. É autor de diversos artigos versando sobre aspectos técnicos e didáticos da Teoria dos Números, publicados na Revista do Professor de Matemática.
Você pode adquirir o livro “Fórmulas
que geram números primos” fazendo seu pedido à Papel Virtual
editora (preço: R$ 17,16
– edição padrão)
[ COMPRAR AGORA ]
O livro também está disponível em formato digital pela metade do preço (R$ 8,58).
Para entrar em contato com o autor do livro, clique aqui e mande sua mensagem.
O livro "Fórmulas que geram números primos" pode ser consultado nas seguintes bibliotecas com o ISBN 85-7493-152-7.
[ Números primos | Fórmulas para primos | O livro]
[ O autor | Como comprar | Entre em contato ]
[ Bibliotecas onde consultar | INÍCIO ]
Última atualização: 15/04/06