Pentomino Fuzion Challenges
 The rectangular
6X10 board has probably been studied the most. There are exactly 2339 different solutions but it is surprisingly
difficult to find one. As a variation try finding a solution where all 12 pentominoes touch the outside perimeter.
Another challenge is to find the maximum number of pentominoes that can be placed in the interior without touching
the perimeter. The solution shown here has 3. There are 32 interior squares which would allow 6 pieces, but clearly
there are not enough long skinny pieces to go single file around the perimeter. Can you find a solution with 4
or more pieces surrounded?
The rectangular
6X10 board has probably been studied the most. There are exactly 2339 different solutions but it is surprisingly
difficult to find one. As a variation try finding a solution where all 12 pentominoes touch the outside perimeter.
Another challenge is to find the maximum number of pentominoes that can be placed in the interior without touching
the perimeter. The solution shown here has 3. There are 32 interior squares which would allow 6 pieces, but clearly
there are not enough long skinny pieces to go single file around the perimeter. Can you find a solution with 4
or more pieces surrounded?
 The rectangular
5X12 board has exactly 1010 different solutions. When using computer programs like Fuzion, duplicate solutions
can be eliminated by placing the X pentomino in the same quadrant every time. The X piece is chosen because it
has only one possible orientation. That is, it fits the same in a puzzle when rotated and flipped-over. Which pentomino
has only two orientations? There are six pentominoes that fit differently for each of the eight possible orientations,
can you find them?
The rectangular
5X12 board has exactly 1010 different solutions. When using computer programs like Fuzion, duplicate solutions
can be eliminated by placing the X pentomino in the same quadrant every time. The X piece is chosen because it
has only one possible orientation. That is, it fits the same in a puzzle when rotated and flipped-over. Which pentomino
has only two orientations? There are six pentominoes that fit differently for each of the eight possible orientations,
can you find them?
 The rectangular 4X15 board has exactly 368 different solutions. The solution
shown has 2 interior rectangles, so 16 different solutions can be
easily made by flipping through box combinations. The 3X20 rectangular board has
only 2 related solutions. The solution isn't shown so you won't be tempted
while working on this challenge. Some people feel the 3X20 solution is easier
to find than one of the 6X10s, contrary to the tale in Arthur Clarke's Imperial
Earth.
The rectangular 4X15 board has exactly 368 different solutions. The solution
shown has 2 interior rectangles, so 16 different solutions can be
easily made by flipping through box combinations. The 3X20 rectangular board has
only 2 related solutions. The solution isn't shown so you won't be tempted
while working on this challenge. Some people feel the 3X20 solution is easier
to find than one of the 6X10s, contrary to the tale in Arthur Clarke's Imperial
Earth.
 Imagine magnifying
a pentomino so each square is divided into a 3X3 grid of 9 equal squares. Do this to each of the 5 pentomino squares
to yield 45 smaller squares. It is now possible to fill the shape with 9 of the 12 pentominoes as shown here. Can
you find a solution to each of the 12 pentomino shapes?
Take a peek
at all 12 solutions. Which pentomino shape has the most solutions? Which has
the fewest? Fuzion's board designer and solver comes in real handy here.
Imagine magnifying
a pentomino so each square is divided into a 3X3 grid of 9 equal squares. Do this to each of the 5 pentomino squares
to yield 45 smaller squares. It is now possible to fill the shape with 9 of the 12 pentominoes as shown here. Can
you find a solution to each of the 12 pentomino shapes?
Take a peek
at all 12 solutions. Which pentomino shape has the most solutions? Which has
the fewest? Fuzion's board designer and solver comes in real handy here.
 A checkers board has 64 squares so if 4 squares are disallowed, pentominoes
should fit around the "holes" on the remaining 60 squares. The
challenge is to place holes making a board that can not be
solved. Excluded are the obvious methods of isolating board squares. For
example placing 4 holes around in a circle with only the corners touching or 3
holes touching corners along the perimeter. In other words it must be possible
to place at least one of the pentominoes in the areas around the holes. Here
is a page full of
checkers board solutions.
To date there are no known unsolvable 4-hole checker boards.
A checkers board has 64 squares so if 4 squares are disallowed, pentominoes
should fit around the "holes" on the remaining 60 squares. The
challenge is to place holes making a board that can not be
solved. Excluded are the obvious methods of isolating board squares. For
example placing 4 holes around in a circle with only the corners touching or 3
holes touching corners along the perimeter. In other words it must be possible
to place at least one of the pentominoes in the areas around the holes. Here
is a page full of
checkers board solutions.
To date there are no known unsolvable 4-hole checker boards.
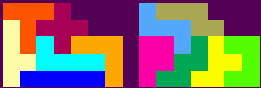 The challenge is to find two identical sections as shown here. When placed on
top of each other they overlap exactly. Each half section will contain 6 of the
12 pentominoes. How many different shapes can you find that duplicate? It is
well known that two 5X6 rectangular shapes can be solved. One visitor
to this site discovered a method of assembling 3 equal sets of pairs
(solution spoiler)
which can be combined to create many duplicates. Can you find any other 3 equal
sets of pairs?
The challenge is to find two identical sections as shown here. When placed on
top of each other they overlap exactly. Each half section will contain 6 of the
12 pentominoes. How many different shapes can you find that duplicate? It is
well known that two 5X6 rectangular shapes can be solved. One visitor
to this site discovered a method of assembling 3 equal sets of pairs
(solution spoiler)
which can be combined to create many duplicates. Can you find any other 3 equal
sets of pairs?
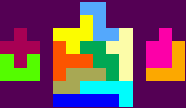 Try to find a family
of shapes as shown here. It is easier to see then explain the rules. The big shape in the middle is twice the size
of the two smaller shapes. Start by finding a shape with 2 pentominoes, then see if you can duplicate it with 2
other pentominoes, finally use the remaining 8 pentominoes to form the double size shape. To date visitors to this
site have found 3 other sets meeting this criteria.
Try to find a family
of shapes as shown here. It is easier to see then explain the rules. The big shape in the middle is twice the size
of the two smaller shapes. Start by finding a shape with 2 pentominoes, then see if you can duplicate it with 2
other pentominoes, finally use the remaining 8 pentominoes to form the double size shape. To date visitors to this
site have found 3 other sets meeting this criteria.
 The solution shown here is a family of three congruent shapes and was given in
Golomb's new Polyominoes book. These solutions are a fun way to store 3D
pentominoes in a compact stack. Fuzion's board designer and auto solver has
found
several more solutions.
Many other probable boards have been ruled-out as unsolvable by Fuzion.
Can you find any more solutions?
The solution shown here is a family of three congruent shapes and was given in
Golomb's new Polyominoes book. These solutions are a fun way to store 3D
pentominoes in a compact stack. Fuzion's board designer and auto solver has
found
several more solutions.
Many other probable boards have been ruled-out as unsolvable by Fuzion.
Can you find any more solutions?
Solutions Library
To get involved in the ever expanding knowledge of polyomino possibilities you can send Email to the Fuzion
Database. If you are playing with Fuzion simply "attach" a copy of the pertinent [].SOL file to your
email. The [].SOL files are located in your Fuzion directory. Each board has a separate solutions file for example
the rectangular 6X10.SOL or the 8X15.SOL file for puzzles made with the board designer. If you are playing manually
you could represent each pentomino with sets of different letters as shown below.

If you have a new challenge, questions, or comments we would be glad to hear from you.
View basic Polyomino statistics
Send Email to the Fuzion Database
Download the latest shareware version 2.8.JAN2000 of Fuzion! (95 kb)
[ FUZION HOME ]
[ CHALLENGES TOP ]
[ LINKS ]
Click on Fuzion Home to transfer to the most current Fuzion site.
This page hosted by
 Get your own Free Home Page
Get your own Free Home Page
 This page was updated on or about 18 APR 01.
This page was updated on or about 18 APR 01.
Designed for viewing with at least 800 x 600 resolution and 256 colors.
Copyright 1997-2001 by Ken Zeltner. All Rights Reserved.
 The rectangular
6X10 board has probably been studied the most. There are exactly 2339 different solutions but it is surprisingly
difficult to find one. As a variation try finding a solution where all 12 pentominoes touch the outside perimeter.
Another challenge is to find the maximum number of pentominoes that can be placed in the interior without touching
the perimeter. The solution shown here has 3. There are 32 interior squares which would allow 6 pieces, but clearly
there are not enough long skinny pieces to go single file around the perimeter. Can you find a solution with 4
or more pieces surrounded?
The rectangular
6X10 board has probably been studied the most. There are exactly 2339 different solutions but it is surprisingly
difficult to find one. As a variation try finding a solution where all 12 pentominoes touch the outside perimeter.
Another challenge is to find the maximum number of pentominoes that can be placed in the interior without touching
the perimeter. The solution shown here has 3. There are 32 interior squares which would allow 6 pieces, but clearly
there are not enough long skinny pieces to go single file around the perimeter. Can you find a solution with 4
or more pieces surrounded?
 The rectangular
5X12 board has exactly 1010 different solutions. When using computer programs like Fuzion, duplicate solutions
can be eliminated by placing the X pentomino in the same quadrant every time. The X piece is chosen because it
has only one possible orientation. That is, it fits the same in a puzzle when rotated and flipped-over. Which pentomino
has only two orientations? There are six pentominoes that fit differently for each of the eight possible orientations,
can you find them?
The rectangular
5X12 board has exactly 1010 different solutions. When using computer programs like Fuzion, duplicate solutions
can be eliminated by placing the X pentomino in the same quadrant every time. The X piece is chosen because it
has only one possible orientation. That is, it fits the same in a puzzle when rotated and flipped-over. Which pentomino
has only two orientations? There are six pentominoes that fit differently for each of the eight possible orientations,
can you find them?
 The rectangular 4X15 board has exactly 368 different solutions. The solution
shown has 2 interior rectangles, so 16 different solutions can be
easily made by flipping through box combinations. The 3X20 rectangular board has
only 2 related solutions. The solution isn't shown so you won't be tempted
while working on this challenge. Some people feel the 3X20 solution is easier
to find than one of the 6X10s, contrary to the tale in Arthur Clarke's Imperial
Earth.
The rectangular 4X15 board has exactly 368 different solutions. The solution
shown has 2 interior rectangles, so 16 different solutions can be
easily made by flipping through box combinations. The 3X20 rectangular board has
only 2 related solutions. The solution isn't shown so you won't be tempted
while working on this challenge. Some people feel the 3X20 solution is easier
to find than one of the 6X10s, contrary to the tale in Arthur Clarke's Imperial
Earth.
 Imagine magnifying
a pentomino so each square is divided into a 3X3 grid of 9 equal squares. Do this to each of the 5 pentomino squares
to yield 45 smaller squares. It is now possible to fill the shape with 9 of the 12 pentominoes as shown here. Can
you find a solution to each of the 12 pentomino shapes?
Imagine magnifying
a pentomino so each square is divided into a 3X3 grid of 9 equal squares. Do this to each of the 5 pentomino squares
to yield 45 smaller squares. It is now possible to fill the shape with 9 of the 12 pentominoes as shown here. Can
you find a solution to each of the 12 pentomino shapes?
 A checkers board has 64 squares so if 4 squares are disallowed, pentominoes
should fit around the "holes" on the remaining 60 squares. The
challenge is to place holes making a board that can not be
solved. Excluded are the obvious methods of isolating board squares. For
example placing 4 holes around in a circle with only the corners touching or 3
holes touching corners along the perimeter. In other words it must be possible
to place at least one of the pentominoes in the areas around the holes. Here
is a page full of
A checkers board has 64 squares so if 4 squares are disallowed, pentominoes
should fit around the "holes" on the remaining 60 squares. The
challenge is to place holes making a board that can not be
solved. Excluded are the obvious methods of isolating board squares. For
example placing 4 holes around in a circle with only the corners touching or 3
holes touching corners along the perimeter. In other words it must be possible
to place at least one of the pentominoes in the areas around the holes. Here
is a page full of
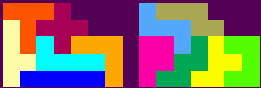 The challenge is to find two identical sections as shown here. When placed on
top of each other they overlap exactly. Each half section will contain 6 of the
12 pentominoes. How many different shapes can you find that duplicate? It is
well known that two 5X6 rectangular shapes can be solved. One visitor
to this site discovered a method of assembling 3 equal sets of pairs
The challenge is to find two identical sections as shown here. When placed on
top of each other they overlap exactly. Each half section will contain 6 of the
12 pentominoes. How many different shapes can you find that duplicate? It is
well known that two 5X6 rectangular shapes can be solved. One visitor
to this site discovered a method of assembling 3 equal sets of pairs
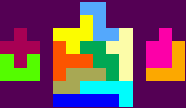 Try to find a family
of shapes as shown here. It is easier to see then explain the rules. The big shape in the middle is twice the size
of the two smaller shapes. Start by finding a shape with 2 pentominoes, then see if you can duplicate it with 2
other pentominoes, finally use the remaining 8 pentominoes to form the double size shape. To date visitors to this
site have found 3 other sets meeting this criteria.
Try to find a family
of shapes as shown here. It is easier to see then explain the rules. The big shape in the middle is twice the size
of the two smaller shapes. Start by finding a shape with 2 pentominoes, then see if you can duplicate it with 2
other pentominoes, finally use the remaining 8 pentominoes to form the double size shape. To date visitors to this
site have found 3 other sets meeting this criteria.
 The solution shown here is a family of three congruent shapes and was given in
Golomb's new Polyominoes book. These solutions are a fun way to store 3D
pentominoes in a compact stack. Fuzion's board designer and auto solver has
found
The solution shown here is a family of three congruent shapes and was given in
Golomb's new Polyominoes book. These solutions are a fun way to store 3D
pentominoes in a compact stack. Fuzion's board designer and auto solver has
found
