/*
Test driver to test linreg.h linear regression class
*/
#include <iostream.h>
#include <iomanip.h>
#include "linreg.h"
double x[] = { 71, 73, 64, 65, 61, 70, 65, 72, 63, 67, 64};
double y[] = {160, 183, 154, 168, 159, 180, 145, 210, 132, 168, 141};
Point2D p[] = { Point2D(71, 160), Point2D(73, 183), Point2D(64, 154),
Point2D(65, 168), Point2D(61, 159), Point2D(70, 180),
Point2D(65, 145), Point2D(72, 210), Point2D(63, 132),
Point2D(67, 168), Point2D(64, 141)};
void main()
{
cout << "Linear Regression Test\n" << endl;
LinearRegression lr(x, y, 11); // create with two arrays
cout << "Number of x,y pairs = " << lr.items() << endl;
cout << lr << endl;
cout << "Coefficient of Determination = "
<< lr.getCoefDeterm() << endl;
cout << "Coefficient of Correlation = "
<< lr.getCoefCorrel() << endl;
cout << "Standard Error of Estimate = "
<< lr.getStdErrorEst() << endl;
cout << "\nLinear Regression Test Part 2 (using Point2Ds)\n" << endl;
LinearRegression lr2(p, 11); // create with array of points
cout << "Number of x,y pairs = " << lr2.items() << endl;
cout << lr2 << endl;
cout << "Coefficient of Determination = "
<< lr2.getCoefDeterm() << endl;
cout << "Coefficient of Correlation = "
<< lr2.getCoefCorrel() << endl;
cout << "Standard Error of Estimate = "
<< lr2.getStdErrorEst() << endl;
cout << "\nLinear Regression Test Part 3 (empty instance)\n" << endl;
LinearRegression lr3; // empty instance of linear regression
for (int i = 0; i < 11; i++)
lr3.addPoint(p[i]);
cout << "Number of x,y pairs = " << lr3.items() << endl;
cout << lr3 << endl;
cout << "Coefficient of Determination = "
<< lr3.getCoefDeterm() << endl;
cout << "Coefficient of Correlation = "
<< lr3.getCoefCorrel() << endl;
cout << "Standard Error of Estimate = "
<< lr3.getStdErrorEst() << endl;
}
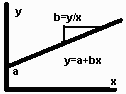 Where y is the dependent coordinate and x is the independent coordinate.
The coefficient a is the value of y when x is zero
and is called the y intercept, and the coefficient b
is the slope of the line or the amount y changes when there is a given
change in x. The slope determines the angle of the line when it is plotted
on a graph.
Where y is the dependent coordinate and x is the independent coordinate.
The coefficient a is the value of y when x is zero
and is called the y intercept, and the coefficient b
is the slope of the line or the amount y changes when there is a given
change in x. The slope determines the angle of the line when it is plotted
on a graph.