

Ing. Eligio Antonio Gutiérres Orellana
TEMA:
Normalización de Bases de Datos
Resumen
Sub tema: Segunda Forma Normal
Formas Normales.
Son las técnicas para prevenir las anomalías en las tablas. Dependiendo de su estructura, una tabla puede estar en primera forma normal, segunda forma normal o en cualquier otra.
Relación entre las formas normales:
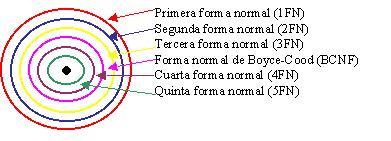
Segunda forma normal:
Para definir formalmente la segunda forma normal requerimos saber que es una dependencia funcional: Consiste en edificar que atributos dependen de otro(s) atributo(s).
Definición formal:
Una relación R está en 2FN si y solo si está en 1FN y los atributos no primos dependen funcionalmente de la llave primaria.
Una relación se encuentra en segunda forma normal, cuando cumple con las reglas de la primera forma normal y todos sus atributos que no son claves (llaves) dependen por completo de la clave . De acuerdo con está definición, cada tabla que tiene un atributo único como clave, esta en segunda forma normal.
La segunda forma normal se representa por dependencias funcionales como:
Nótese que las llaves primarias están representadas con doble cuadro, las flechas nos indican que de estos atributos se puede referenciar a los otros atributos que dependen funcionalmente de la llave primaria.
Una relación está en segunda forma normal (2FN) solamente si todos los atributos son dependientes en forma completa de la clave.
Descripción De La Segunda Forma Normal (2 Fn)
Su nombre ya nos indica el hecho de que la segunda forma normal es por lo general el próximo paso de normalización y descomposición. Para ser accesible a la normalización, y poder ser puesta en segunda forma normal, la relación debe poseer las siguientes propiedades:
• Debe estar en primera forma normal
• Debe tener una clave compuesta.
La consecuencia inmediata de los requerimientos expresados más arriba es que cualquier relación en primera forma normal que tiene una clave simple, está automáticamente en segunda forma normal. Comencemos con un ejemplo en forma de tabla de una relación consistente en 17 atributos, que se presenta en la figura. La misma se encuentra en primera forma normal y tiene una clave compuesta que consiste en dos atributos P y Q. Estos están subrayados en la figura para mostrar que sirven como clave. La tupla de relación puede también escribirse linealmente en forma simbólicamente:
R = (A,B,C,D,E,F,G,H,I,L,M,N,O,P,Q)
El próximo paso es crear un grafo de dependencia, presentando aquí como figura. Debe notarse que este grafo se crea examinado con conocimientos y atributos para determinar como participan y relacionan entre ellos.
No resulta suficiente analizar la matríz de relación, la cual puede hacernos creer que existe una dependencia debido a que la muestra de la cual se ha extraído dicha relación es pequeña. Si somos inducidos a error por los datos existentes y construimos una dependencia donde esta no existe, se planteará un problema. Cuando lleguen nuevos datos que contradigan la dependencia, deberá dejarse de lado el esquema completo.
Supongamos en consecuencia que el grafo que se puede observar en la figura ha sido derivado en forma funcional y que expresa correctamente las dependencias. Resulta claro a partir de este grafo que los atributos que parten de P son dependientes solamente de este. De un modo similar los que parten de Q dependen solamente de este último. Solamente aquellos que parten de la línea de trazos que conecta a P y Q tienen dependencia completa de ambos. Esta es la guía para la descomposición.
Descomposición
La figura contiene 3 sub-árboles, la base de nuestra descomposición. Definimos una subtupla general en base a cada sub-árbol y en consecuencia:
P' = (P,A,B,C,E,H,K)
Q' = (Q,F,G,J,N)
PQ = (P,Q,D,I,L,M,O)
Aquí la raíz de los sub-árboles de la izquierda y la derecha. P y Q, se convierte en la clave de sus respectivas subtuplas; ambos. P y Q forman la clave compuesta para la subtupla PQ.
Proyección
El próximo paso es proyectar la relación R sobre cada una de estas subtuplas para formar tres nuevas relaciones, y en consecuencia.
P' = proyectar R(P')
Q' = proyectar R(Q')
PQ = proyectar R(PQ)
Las relaciones así formadas nos dan tres nuevas sub-relaciones. Una subrelación es la relación que deriva de una relación mayor. Las subrelaciones ilustradas en la figura están correlacionadas por medio de los componentes de sus claves. La clave compuesta P y Q de la relación original R. es también la clave de la sub-relación PQ. P y Q tienen a P y Q respectivamente como claves. La línea de trazos en la figura indica que Q está correlacionada con PQ por medio de la componente Q y P está correlacionada con PQ por medio de P.
Para restablecer la relación original R debemos juntar estas tres subrelaciones en algún orden, indicado simbólicamente como:
R = juntar P [juntar PQ, (Q)] (P) = juntar Q[juntar PQ P(P)] (Q).
Grafos
La nueva sub-relación que se ve en la figura se presenta en forma de grafo en la figura siguiente. Existe una considerable analogía entres estas figuras y la figura anterior. Lo importante es la diferencia. En PQ existe una línea de trazos que conecta los componentes de la clave compuesta P y Q en el centro de la figura. Los arcos parten del centro de esta línea de trazos hacia todos los componentes de P y Q, los cuales son dependientes en forma completa de ambos, es decir de P y Q. Una línea de puntos conecta P en la relación PQ a P de la relación P. Esto representa la correspondencia entre ambas veces P. Una línea de puntos conecta de un modo similar Q en PQ a Q en Q para indicar una correspondencia similar.
Efectos
El efecto de esta descomposición puede no resultar inmediatamente claro. Debemos insistir en que ninguna relación correcta debe contener tuplas duplicadas. La relación original R contiene muchas subtuplas duplicadas P' y Q'. Las mismas han sido eliminadas durante la descomposición. Esto facilita en forma extraordinaria la actualización y otras importantes operaciones que afectan a estas relaciones, las cuales serán aclaradas en los ejemplos que siguen.
Ejemplo de inventario
Vamos a utilizar ahora un ejemplo práctico para demostrar la normalización. En la figura se observa una parte de la matríz de relación PW.
Pueden verse los nombres de los atributos simbólicos y sus significados, pero no sus valores. Las columnas no aparecen en ningún orden en particular. Debe observarse la clave compuesta que distingue cada tupla, que abarca el número de pieza y el número de depósito PNO y WNO.
Arbol de Dependencia
El medio para descomponer la relación es el árbol de dependencia que se ve en la figura. Este árbol ha sido construido solamente teniendo en cuenta la dependencia completa, y no muestra las dependencias total o transitiva, que se describe más adelante, si es que las mismas existen.
Como podíamos esperar, aparecen tres sub-árboles. El sub-árbol de la izquierda, con raíz PNO, contiene los atributos que se aplican solamente a la pieza o parte. El sub-árbol de la derecha con raíz WNO describe cada depósito. EDl sub-árbol del centro corresponde a las partes y al depósito, y describe la cantidad de partes disponibles en el depósito, QOH, y el número de cajón o estante, BIN (o algún otro parámetro de ubicación), donde dichas partes pueden ser halladas.
El próximo paso es definir tres tuplas generales para cada sub-árbol,
P = (PNO, DESC, PR, UNIT)
W = (WNO, WAD, FUE)
P/W = (PNO, WNO, BIN, QOH)
La descomposición consiste en proyectar la relación PW sobre cada una de estas tuplas para obtener tres nuevas sub-relaciones:
P = proyectar PW(P)
W = proyectar PW(W)
P/W = proyectar PW(P/W)
La descomposición en la figura muestra las tres relaciones como matrices; la línea de trazos indica como se vinculan las relaciones.
Efecto
Discutiremos ahora algunas de las ventajas obtenidas mediante la descomposición. Si estas relaciones se utilizan para el control de inventario. nuestra preocupación será cuantas piezas de cada tipo están disponibles en un depósito en particular. Cuando se retiran piezas o se reciben nuevos envíos la cantidad disponible, QOH será la variable de cambio. La actualización consiste en poner al día sub-relación P/W la cual ahora contiene solamente malos componentes en lugar de los nuevos P/W.
Existe una tupla P en la sub-relación de pieza o parte, P, para cada parte y una tupla. W, en la sub relación W, para cada depósito y estos últimos probablemente no serán muchos. Consideremos la facilidad de efectuar cambios en un depósito en particular. Si un atributo de uno de los depósitos varía entraremos en W para efectuar el cambio solamente en una tupla. En la primera forma normal para PW teníamos que encontrar todas las tuplas en las cuales el valor de WNO esta el particularmente deseado, y efectuar el mismo cambio en cada una de ellas. Si dicho depósito almacenaba 100 partes, como consecuencia debía variar 100 tuplas de PW. El procedimiento de actualización se aplica también a las descripciones de partes. Si el precio de alguna parte o pieza cambia, este cambio es independiente del depósito en el cual se almacena dicha parte. Solamente se efectúa un cambio en P a diferencia de los muchos que hubieran sido requeridos para PW.
Infografía