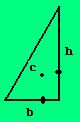
Bonus: For a calculus exercise, recheck your answer using integration.
Using the theorem of Pappus, first we imagine the rotation of the triangle about the y-axis, where the b and h lie on the x and y axis respectively. The centroid travels 2π*xav where xav is the x coordinate of the centroid. Hence, from the theorem:
2π*x*bh/2 = π*b2h/3. The right hand side is the volume of the cone generated.
From this we get xav = b/3. Similarly and symmetrically, we get yav = h/3. Thus the centroid of a right triangle of base b and height h is (b/3, h/3).
To actually find the centroid, one has to integrate. We use double integrals for areas. Let D be the density of the triangle, mass per unit length. Assuming uniformity, we have D=M/A = 2M/(bh). So, we find the double integral of (2M)/(bh) * x dA where y goes from 0 to -hx/b+h and x from 0 to b. This results in the same answer for xav. Similary yav can be found.