Basic Properties

Basic Properties
Calculus I
Calculus II
Chemistry
Physics
Oceanography

By Rick Stoll

To start out with, let us note that the limit, when it exists, is unique. That is why we say "the limit", not "a limit". This property translates formally into:

$\begin{displaymath}\mbox{if}\;\; \lim_{x \rightarrow a} f(x) = K\;\; \mbox{and}\... ...im_{x \rightarrow a} f(x)= L\;\;,\;\; \mbox{then}\;\; K = L\;. \end{displaymath}$

Most of the examples studied before used the definition of the limit. But in general it is tedious to find the $\delta$ given the $\varepsilon$ . The following properties help circumvent this.

Theorem. Let f(x) and g(x) be two functions. Assume that

$\begin{displaymath}\lim_{x \rightarrow a} f(x) = K\;\; \mbox{and}\;\; \lim_{x \rightarrow a} g(x)= L\;.\end{displaymath}$

Then

(1): $\displaystyle \lim_{x \rightarrow a} f(x) + g(x) = K + L$ ;
(2): $\displaystyle \lim_{x \rightarrow a} \alpha f(x) = \alpha K$ , where $\alpha$ is an arbitrary number;
(3): $\displaystyle \lim_{x \rightarrow a} f(x)\cdot g(x) = K\cdot L$ .

These properties are very helpful. For example, it is easy to check that

$\begin{displaymath}\lim_{x \rightarrow a} 1 = 1\;\; \mbox{and}\;\; \lim_{x \rightarrow a} x= a\end{displaymath}$

for any real number a. So Property (3) repeated implies

$\begin{displaymath}\lim_{x \rightarrow a} x^n = a^n\end{displaymath}$

and Property (2) implies

$\begin{displaymath}\lim_{x \rightarrow a} \alpha = \alpha\;.\end{displaymath}$

These limits combined with Property (1) give

$\begin{displaymath}\lim_{x \rightarrow a} P(x)= P(a)\end{displaymath}$

for any polynomial function $P(x) = a_nx^n + \cdots + a_1 x + a_0$ .

The next natural question then is to ask what happens to quotients of functions. The following result answers this question:

Theorem. Let f(x) and g(x) be two functions. Assume that

$\begin{displaymath}\lim_{x \rightarrow a} f(x) = K\;\; \mbox{and}\;\; \lim_{x \rightarrow a} g(x)= L\;.\end{displaymath}$

Then

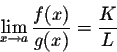
$\begin{displaymath}\displaystyle \lim_{x \rightarrow a} \frac{f(x)}{g(x)} = \frac{K}{L}\end{displaymath}$

provided $L \neq 0$ .

This implies immediately the following:

$\begin{displaymath}\lim_{x \rightarrow a} \frac{P(x)}{Q(x)} = \frac{P(a)}{Q(a)}\;,\end{displaymath}$

where P(x) and Q(x) are two polynomial functions with $Q(a) \neq 0$ .

Example. Assume that

$\begin{displaymath}\lim_{x \rightarrow 0} \frac{\sin(x)}{x} = 1\;\; \mbox{and}\;\; \lim_{x \rightarrow 0} \cos(x)= 1\;.\end{displaymath}$

Find the limit

$\begin{displaymath}\lim_{x \rightarrow 0} \frac{1 - \cos(x)}{x^2} = \frac{1}{2}\;\cdot\end{displaymath}$

Answer. Note that we cannot apply the result about limits of quotients directly, since the limit of the denominator is zero. The following manipulations allow to circumvent this problem. We have

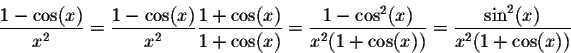
$\begin{displaymath}\frac{1 - \cos(x)}{x^2} = \frac{1 - \cos(x)}{x^2} \frac{1 + \... ...^2(x)}{x^2 (1 + \cos(x))} = \frac{\sin^2(x)}{x^2 (1 + \cos(x))}\end{displaymath}$

Using the above properties we get

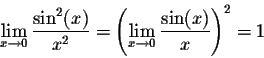
$\begin{displaymath}\lim_{x \rightarrow 0} \frac{\sin^2(x)}{x^2}= \left(\lim_{x \rightarrow 0} \frac{\sin(x)}{x}\right)^2 = 1\end{displaymath}$

and

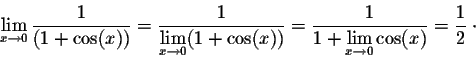
$\begin{displaymath}\lim_{x \rightarrow 0} \frac{1}{(1 + \cos(x))} = \frac{1}{\di... ...ystyle 1 + \lim_{x \rightarrow 0} \cos(x)} = \frac{1}{2}\;\cdot\end{displaymath}$

Hence

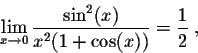
$\begin{displaymath}\lim_{x \rightarrow 0} \frac{\sin^2(x)}{x^2 (1 + \cos(x))} = \frac{1}{2}\;,\end{displaymath}$

which gives the limit

$\begin{displaymath}\lim_{x \rightarrow 0} \frac{1 - \cos(x)}{x^2} = \frac{1}{2}\;\cdot\end{displaymath}$

Exercise 1. Find the limit

$\begin{displaymath}\lim_{x \rightarrow 1} \frac{x^2 - 3x +2}{x-1} \;\cdot\end{displaymath}$

Answer.

Exercise 2. Evaluate

$\begin{displaymath}\lim_{x \rightarrow 3} \left(\frac{1}{x} - \frac{1}{3}\right)... ...} \left(\frac{1}{x} - \frac{1}{3}\right) \frac{1}{(x-3)}\;\cdot\end{displaymath}$

Answer.

Let us continue to list some basic properties of limits.

Theorem. Let f(x) be a positive function, i.e. $f(x) \geq 0$ . Assume that

$\begin{displaymath}\lim_{x \rightarrow a} f(x) = L\;.\end{displaymath}$

Then

$\begin{displaymath}\lim_{x \rightarrow a} \sqrt{f(x)} = \sqrt{L}\;.\end{displaymath}$

This is actually a special case of the following general result about the composition of two functions:

Theorem. Let f(x) and g(x) be two functions. Assume that

$\begin{displaymath}\lim_{x \rightarrow a} f(x) = K\;\; \mbox{and}\;\; \lim_{x \rightarrow K} g(x)= L\;.\end{displaymath}$

Then

$\begin{displaymath}\lim_{x \rightarrow a} \left(g \circ f\right)(x) = L\;.\end{displaymath}$

Example. Geometric considerations imply

$\begin{displaymath}\lim_{x \rightarrow 0} \sin(x) = 0\;.\end{displaymath}$

Since $\cos(x) > 0$ for x close to 0, then we have

$\begin{displaymath}\cos(x) = \sqrt{1 - \sin^2(x)}\end{displaymath}$

which implies

$\begin{displaymath}\lim_{x \rightarrow 0} \cos(x) = 1\;.\end{displaymath}$

Using the trigonometric identities

$\begin{displaymath}\left\{\begin{array}{lcl} \sin(a+b) &=& \sin(a) \cos(b) + \si... ...+b) &=& \cos(a) \cos(b) - \sin(b) \sin(a)\;, \end{array}\right.\end{displaymath}$

we obtain

$\begin{displaymath}\lim_{x \rightarrow a} \sin(x) = \sin(a)\;\; \mbox{and}\;\; \lim_{x \rightarrow a} \cos(x)= \cos(a)\;.\end{displaymath}$

Back to the top of page

Send mail to m_engineer2002@netzero.com with questions or comments about this web site. Copyright © 2001 Math Depot Last modified: April 27, 2001

Send mail to m_engineer2002@netzero.com with questions or comments about this web site.
Copyright © 2001 Math Depot
Last modified: April 27, 2001