Finding
Rational Zeros of Polynomials
Factor Theorem
If  is a zero of the polynomial
is a zero of the polynomial 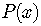 ,
,
then 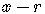 is
a factor of
is
a factor of 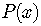 .
.
Conversely, if 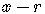 is a factor of
is a factor of 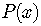 .
.
then  is a zero of
is a zero of 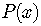 .
.
By the Division Algorithm
 .
.
By the Remainder Theorem
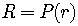 .
.
If  is a zero of
is a zero of 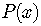 ,
then
,
then  ,
so
,
so 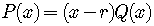 .
.
In words this says that 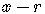 is a factor of
is a factor of 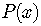 .
.
Conversely, if  is a factor of
is a factor of 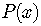 ,
we can write
,
we can write
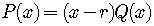 .
.
Then
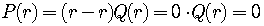
which says that  is a zero of
is a zero of 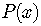 .
.
See Example 1, pages 298 - 299.
The Fundamental Theorem of Algebra
Every polynomial of degree 
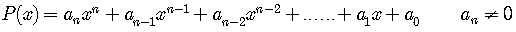
has at least one zero.
This theorem implies that
Every polynomial of degree  has exactly
has exactly  zeros.
zeros.
Example
 has exactly 2 zeros.
has exactly 2 zeros.
 has exactly 17 zeros.
has exactly 17 zeros.
The zeros are not necessarily distinct.
 has 2001 zeros.
has 2001 zeros.
The zero  occurs
2001 times.
occurs
2001 times.
4 is said to be a root of multiplicity 2001.
Example
Factor 
and solve the equation  .
.
The first step is, essentially, trial and error as we search
for a linear factor of  of the form
of the form
 .
.
Try 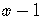 .
.
Use synthetic division to see if 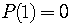 .
.
 first line
first line
 second line
second line
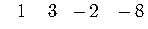 third line is the quotient and the remainder is the
last number
third line is the quotient and the remainder is the
last number
 ,
,
not  ,
so
,
so 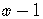 is not a factor and
is not a factor and 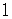 is not a solution of the equation.
is not a solution of the equation.
Next, try 
or  in the form
in the form 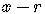 ,
so
,
so  .
.

Since  ,
we know that
,
we know that  is one factor,
is one factor,
 .
.
The coefficients of the quotient are given by the numbers on the third line,
except for the last number, 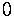 ,
which is the remainder.
,
which is the remainder.
Since the dividend 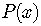 is a third degree polynomial
is a third degree polynomial
and the divisor  is a first degree polynomial,
is a first degree polynomial,
the quotient must be a second degree polynomial,
and the first three numbers on the third line

must be the coefficients of that second degree polynomial.
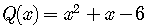 .
.
So
 .
.
 is easily factored as
is easily factored as 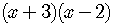 .
.
 is the complete factoring.
is the complete factoring.
To solve the equation  ,
use the Zero Product Principle.
,
use the Zero Product Principle.
Set each factor equal to zero and solve the equations.

So the solutions are

NOTE: If the quadratic  is not easily factorable,
is not easily factorable,
use the quadratic formula

to solve the equation  .
.
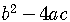 is called the discriminant.
is called the discriminant.
See Example 2, page 301.
Complex Zeros
In the quadratic formula, when the discriminant is less than zero
the roots of the quadratic equation are complex conjugate numbers.
Example
The roots of
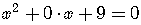
where 
are the complex conjugate numbers
 .
.
Complex Zeros Theorem
Complex zeros, if they exist, of a polynomial with real coefficients
occur in conjugate pairs.
Example
If  is a root then
is a root then  also is a root, and vise versa.
also is a root, and vise versa.
If a polynomial with real coefficients is of odd degree
- for example,  -
-
it could have three real zeros.
However, if it has one complex zero then automatically it has another
complex zero, namely, the complex conjugate.
That make two zeros. We know the polynomial must have exactly three zeros.
So the remaining zero must be real, otherwise, there would be two more
complex roots and the total number of zeros would be four, which is impossible.
This result is the
Odd-Degree Polynomial Real Zero Theorem
A polynomial of odd degree with real coefficients has at least one real zero.
Rational Zeros Theorem
If the polynomial with integer coefficients
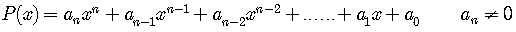
has a rational zero, reduced to lowest terms,
 ,
,
then  must be a factor of
must be a factor of  and
and  must be a factor
of
must be a factor
of  .
.
Note that these theorem only says that if a polynomial has a rational zero
it must be on the list of possible rational zeros given by the theorem.
If we check each number on the list and none of then are zeros,
that only means that the polynomial has no rational roots.
The zeros must then be either irrational numbers or complex numbers.
Example
 has no rational roots.
has no rational roots.
Its roots are the irrational numbers  .
.
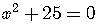 has no rational roots.
has no rational roots.
Its roots are the complex conjugate numbers 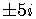 .
.
See Examples 3 - 5, pages 304 -307.
top
next Approximating
Real Zeros of Polynomials


