Proofs

Once you get the hang of them, Proofs are one of the easiest things to understand in Geometry.  Proofs are written with the knowledge of what will come next.  To do that, you have to actually visualize how to do it before you actually write it.  So, in order to write a proof, you have to think backwards.  Most of the time, it's pretty easy.  Sometimes, though, you must use many steps to reach your ultimate conclusion.  In these cases, it helps to think through your steps throughout the entire proof before you write them down.  Often, you may have to use many different conjectures and proofs to reach your conclusion.  There are also multiple methods of doing a single proof, so your proof may be different than the one you friend of classmate wrote.

There are three types of proofs in geometry: 2 Column Proofs, Flowchart Proofs, and Paragraph Proofs.  Each is written in a different format.  You can write a single proof with the same steps, and it could be a 2 Column proof, a Flowchart proof, or a paragraph proof.  Because of the fact that you need to be familiar with each format, Mrs. Jones may ask you to write one in a different format from what you normally write.  Trust me, it is well worth it to master each format, since you are sometimes asked to write a specific type of proof on a test.

In every proof, the reasons are the conjectures you have learned and/or the main ideas.  The statements are the arguments you're making.  Proofs are almost like an argument with a friend -- you can say "Bob, you're a liar!" and Bob knows that you think that he's a liar.  But for him to believe that he is actually a liar, you have to say "Bob, you're a liar because you said that you didn't have the to-do-list!"  Now, Bob knows that you have justification to believe that he's a liar -- because he said that he didn't have the list, even though he really did!  It works the same way in proofs -- if you say something, and don't have anything to back it up, then you can't argue that you're right, can you?  That's why proofs work as a way to get messages across to others about why a mathematical fact is true.  Because the conjectures and theorems are all the same, no matter what you call them, or how you say them, the reader of your proof will know that what you're saying is true if the reason is a legitimate and it applies to the situation.

Let's start with the most straightforward type of proof.

2-Column Proofs

The above example is an idea of what a 2-Column Proof should look like.  As you can see, the first reason is always listed as Given.  Usually, you're just trying to prove a specific case of a proof.  Sometimes, however, you're asked to prove a conjecture or a theorem.  In these cases, you must use the generic form of a proof.  This means that you must not use numbers -- you must use just the bare angles and segments, ect.  You'll see what I mean in the nezt proof.  The 2-Column proof is the simplest of all the proofs you'll learn.

Paragraph Proofs

Paragraph proofs are for those of us who like to write.  They're just simple paragraphs -- to do one in paragraph form, you write everything like it happens - you write what occurs to you in proving something the moment it comes to mind.  Well, it's not exactly like that, but I think you understand.  In a paragraph proof, you write the given first like most every other proof, and state the given information.  Then, you go on writing the proof, and finish off with the box-slash-slash or QED.

Flowchart Proofs

Flowchart proofs are another easy proof.  For these, you write your statements in numbered boxes and write the reason underneath them.  Use arrows to connect the boxes.  However, make separate boxes for each given statement.  You also need to connect the boxes.  But in flowchart proofs, the arrows used to do this are not from and to consecutive-numbered boxes.  You need to take care to only connect boxes that directly resulted in anothers statement.  So, in my example, you wouldn't connect boxes Box 3 and 5 directly; instead, you would connect Box 3 to Box 4 to Box 5.  This is because the information in Box 3 did not directly result in the information in Box 5, it indirectly influenced Box 5.  So be careful connecting boxes in flowchart proofs -- and if you're not sure about a box, then it probably didn't directly influence the information of the other box!

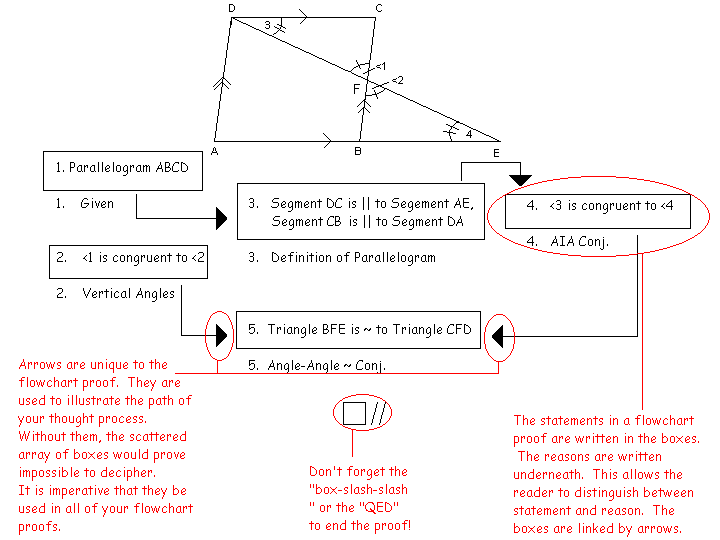Contradiction Proofs (Indirect Proofs)

Contradiction proofs are the proofs I had the most difficulty with.  They are actually proofs that do things backwards, in a sense.  In a contradiction proof, the first step is not to state the given (that's actually the 2nd in this case), but to state something that is false!  When you do a contradiction proof, in the given, you are usually told that two parts of the diagram are not congruent.  In the first step, you state the opposite of what that given statement says.  That step would then be to say that the two parts are congruent!  Then, you go on to prove a proof by contradiction.  This means that, using your assumption as you would normally use a given, along with the other givens.  So you now have to prove a contradiction to a given fact, an opposite to it, one that totally refutes it's counterpart and vice versa.  In doing this, you prove your assumption false, as you write in your paragraph (we'll talk about that later).  This then, because they are totally opposite, proves that the two parts of the diagram are indeed not congruent.  In your paragraph, you'll state that you have reached a contradiction to a given statement and what both the contradiction and the given statement are.  Then, you'll have to say that you argued logically and that therefore, your assumption must be false.  Then, you should state what the false assumption was one more time, then go on to say the true statement and point out that you have proved it true.  Finally-you're done!

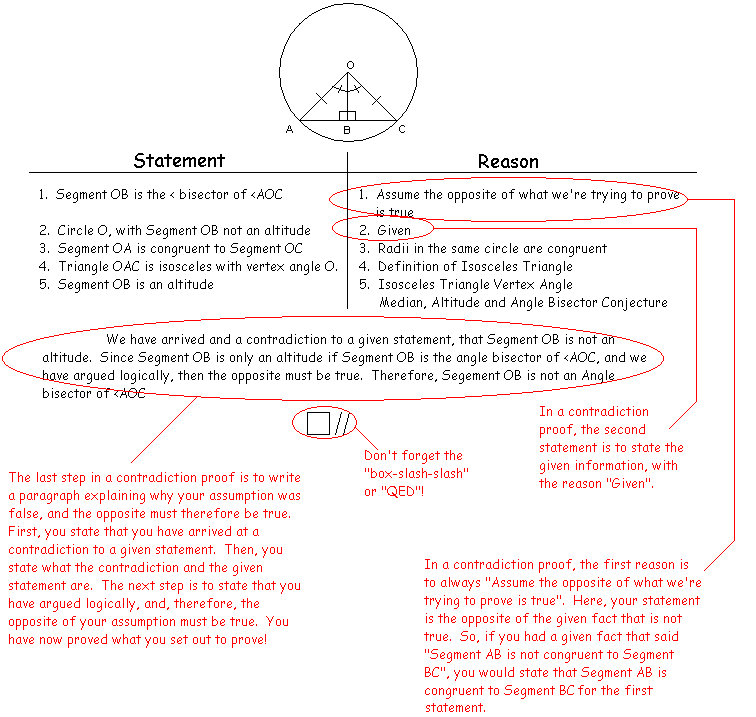TRY SOME OF YOUR OWN

Home

Key of Common Proof Symbols