Propiedades Conmutativas
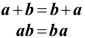
Propiedades Asociativas
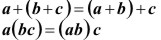
Elemento Neutro
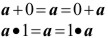
Inverso
Para cada número real a, existe un número real denotado por -a, tal que
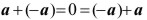
Para cada número real  , existe un número real denotado por 1/a, tal que , existe un número real denotado por 1/a, tal que
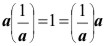
Definición de a-1
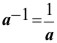
Propiedades distributivas
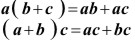
Si a = b entonces a + c = b + c
Si a = b entonces ac = bc
a·0 = 0 para todo número real
Si ab = 0 entonces a = 0 ó b = 0
Propiedades de los negativos

Definición de la resta
La operación de resta (denotada por -) se define como

Definición de la división
Si  entonces la división (denotada por entonces la división (denotada por 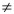 ) se define como ) se define como

Propiedades de los cocientes

Ley de los signos (I). Si a y b tienen el mismo signo, entonces ab y a / b son positivos.
Ley de los signos (II). Si a y b tienen signos opuestos, entonces ab y a / b son negativos.
Definición. Si a es un número real, entonces el valor absoluto |a| de a se define como


Definición
Si n es cualquier entero positivo, entonces
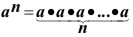
El entero n se le llama exponente.
Leyes de los exponentes
Si a y b son números reales y, m y n son enteros positivos, entonces

Definición del exponente cero. Si a es cualquier número real distinto de cero, entonces a0 = 1
Definición de los exponentes negativos. Si a es un número real distinto de cero y n es un entero positivo, entonces
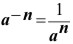
Definición de 

Definición de 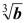

Definición de 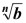
Si a y b son números reales no negativos y si n es un entero positivo, o si a y b son negativos y n es un entero positivo impar, entonces


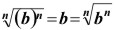
Leyes de los radicales

Si x es cualquier número real, entonces 
Definición de 
Si b es un número real, n es un entero positivo, y 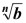 existe, entonces existe, entonces

Definición de los exponentes racionales
Si m / n es un número racional, donde m y n son enteros positivos, y si b es un núemero real tal que 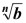 existe, entonces existe, entonces

Comentarios: ollin_tlatoa@yahoo.com.mx
|