Introduction

Definition of a Point

A point can be represented in 2D space as a a pair of numbers, one for each of the x and y axis:

Distance Between Two Points

The distance between two points <Ax,Ay> and <Bx,By > can be found using the pythagorus theorem:

dx = Ax-Bx 

dy = Ay-By 

distance = sqrt(dx*dx + dy*dy)

Definition of a Vector

A vector can be thought of in two ways: either a point at <x,y> or a line going from the origin <0,0> to the point <x,y>, in most cases they're best thought of as the latter. In either case a 2D vector can be represented with 2 scalar values x and y.

Vectors are often used to describe direction. If we take a 2D point at <5,5> and add a 2D vector <4,-4> to it then we get a new point:

Note that we've simply moved the point at <5,5> in the direction <4,-4>.

Vectors themselves can be added by adding each of their components, or they can be multiplied (scaled) by multiplying each component by some constant k (where k <> 0). Scaling a vector by 2 (say) will still cause the vector to point in the same direction, but it will now be twice as long. Of course you can also divide the vector by k (where k <> 0) to get a similar result.

To calculate the length of a vector we simply calculate the distance between the origin and the point at <x,y> :

length = | <x,y> - <0,0> |

       = sqrt( (x-0)*(x-0) + (y-0)*(y-0) ) 

       = sqrt(x*x + y*y)

The square root function is horrendously slow, so try to avoid calculating vector lengths whenever you can. A common problem in computer graphics is to find the shortest vector in a list, in this case you only need to calculate (x*x + y*y) for each of them and find the smallest value from that (since the vector with the shortest length will also have the smallest squared length).

Often in computer graphics you need to convert a vector to a unit vector, ie a vector that points in the same direction but has a length of 1. This is done by simply dividing each component by the length:

Let <x,y> be our vector, length = sqrt(x*x + y*y)

Unit vector =   <x,y>     = |   x      ,      y   | 

               length       | length       length | 

(where length = |<x,y>| )

Note that if the vector is already a unit vector then the length will be 1, and the new values will be the same as the old.

Definition of a 2D Line

There are a few different ways of storing a line, the method to use depends on your application.

First we can imagine a line as having 2 endpoints in 2D space:

P1=<x1,y1> and 

P2=<x2,y2>.

Alternatively we can imagine the line as having an origin (starting point) and a direction (vector):

Origin = <Xo, Yo > 

Direction = <Xd, Yd >

It's simple to convert between these two formats, if we have a line defined by two endpoints then we can assume that the line's origin is at one endpoint and it's direction is the difference between both endpoints:

Origin = P1 = <x1, y1 > 

Direction = P2-P1 = <x2-x1, y2-y1>

Calculating the length of the line can be done by simply calculating the length of the direction vector, ie the distance between the two endpoints.

The origin/direction method (also known as the parametric representation) is particularly handy when you need to find the coordinates of a given point on a line. The equation to do this is:

<x,y> = <xo, yo> + k * <xd, yd>

where k is some scalar value. Setting k to 0 will return the first endpoint, setting it to 1 will return the second endpoint. If you want to find a point halfway along the line then simply set k to 0.5, similarly setting k to 2 will return a point on the line that is twice as far from P1 as P2 is. In computer graphics you often have to find intersections between lines and other objects (such as other lines, planes, cubes etc). These intersection equations often return a k value for the point of intersection, and you have to plug this value into the above equation to get the actual 3D coordinates for the point of intersection. If these functions return a k value where 0 <= k <= 1 then you know the intersection occurred on the line somewhere between the endpoints P1 and P2 (or on them).

The 2D Dot Product

The 2D dot product between two 2D vectors <Ax,Ay> and <Bx,By> is calculated like so:

A * B = Ax*Bx + Ay*By

If A and B are unit vectors then the dot product is the cosine of the angle between them, so the angle itself (theta) can be calculated by taking the inverse cosine of the dot product:

theta = invcos(A * B)

Fortunately you'll often only need the cosine of the angle between 2 vectors and not the angle itself, so the expensive step of calculating the inverse cosine can be skipped.

2D Rotation

A point <x,y> can be rotated around the origin <0,0> by running it through the following equations to get the new point <x',y'> :

x' = cos(theta)*x - sin(theta)*y 

y' = sin(theta)*x + cos(theta)*y

where theta is the angle by which to rotate the point.

Clockwise/Anti-clockwise

The dot product and rotation equations give us a handy way of determining whether the points in a given polygon are stored in clockwise or anti-clockwise fashion.

If we are dealing with a concave polygon then we only need the first 3 points to determine the polygon's orientation. Consider the polygon below:

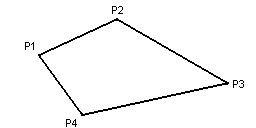
By looking at it we can see that the points are stored clockwise, but we need a method for an application to determine this mathematically. To do this we take the first 3 points:

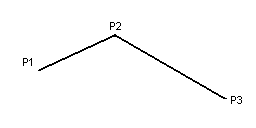
The next step is to calculate the directional value of each edge (the actual position of the polygon doesn't matter). The two edges will thus be:

E1 = P1-P2 

E2 = P3-P2

We can now test the angle between these two edges, ie the angle at P2. If this angle is between 0 and 180 degrees then we know the points appear clockwise.

However, if we rotate E2 anti-clockwise by 90 degrees then we can test whether the angle is between -90 and +90 degrees. The cosine of all angles between this range is between 0 and 1, and the cosine can easily be obtained by taking the dot product.

We know from above that we can rotate a point by -90 degrees with the following formula:

x' = (cos(-90) * x) - (sin(-90) * y) = y 

y' = (sin(-90) * x) + (cos(-90) * y) = -x

Thus we can use the following formula to determine if the 3 points are in clockwise order:

E1x = P1x-P2x 

E1y = P1y-P2y 

E2x = P3x-P2x 

E2y = P3y-P2y

if ((E1x * E2y - E1y * E2x) >= 0) clockwise = TRUE; 

else clockwise = FALSE;

This technique (ie rotate one vector anti-clockwise by 90 degrees and take the dot product between both vectors) is known as the 2D cross product. The 3D cross product also has some useful properties and is disccused further in the article on basic 3D math.

Circles

If the circle is centered on the origin <0,0> and R is the radius then the circle is represented by the following equation:

x*x + y*y - R*R = 0

Thus any point <x,y> lies on the circle if it satisfies this equation. If x*x + y*y - R*R < 0 then we know the point is inside the circle. Similarly, if x*x + y*y - R*R > 0 we know it is outside.

Degrees and Radians

Ellipses

Triangles

Convex And Concave Shapes

Copyright (c) 1997 Mark Feldman (pcgpe@oocities.com) - All Rights Reserved

This article is part of The Win95 Game Programmer's Encyclopedia

Please retain this footer if you distribute this file.

Back to Graphics