Principle Foundations      Home Page

Test of Significance

(Statistical Inference)

     In order to test for the statistical significance of the parameter estimates of the regression, we have firstly to know a few basic things about . The most notable, are the following:  

Statistical inference

Testing the significance of β₁

Example 1:  

     Suppose we have the population relationship of the type  

      Y_i = α + βX_i + ε_i       for all i, 

where the dependent variable is linearly dependent on the explanatory X variable, but is also influenced by the disturbance ε. Thus, by considering this population relationship, if β=0 in this equation then X does not influence Y, which then has an expected value of α, from which it can only be disturbed by a non-zero ε. If , then this means that X does influence Y. We can therefore test whether X influences Y by setting up the null hypothesis H₀: β=0 and testing it against an alternative hypothesis H_A: . We can obtain a test statistic for this purpose. Thus, we apply the formula , which has a Student's t distribution with n-2 d. f (degrees of freedom). We can therefore use a 

                                                                                                       (1.7)

as a test statistic and reject the null hypothesis β=0 (X does not influence Y) if the absolute value of this test statistic exceeds the relevant critical value taken from Student's t tables.

Effectively what we do is to consider whether the OLS estimate  is sufficiently different from zero for us to reject the null hypothesis that the true β is non-zero. Dividing  by its estimated standard error enables us to use Student's t tables to decide what is meant by "sufficiently different".  

Example 2:

     Again taking the example of the household consumption function H₀:  

implies that a household's income does not influence its consumption. Since if β is non-zero we expect β>0 in this case, we employ an upper tail test. That is, the alternative hypothesis is H_A: β>0. Taking the 0.05 level of significance, the critical t value is t_0.05= 1.714 (d.f = n-2). We suppose we have n=25 (hence 23 d.f),  and , so that the test statistic  (1.7) takes a value of 7.19. This clearly exceeds the critical value , so we can reject the null hypothesis β=0 at the 0.05 level of significance and conclude that household income influences consumption. It is possible to test a null hypothesis 

H₀: α=0 in a similar manner. Under this null hypothesis we have that  has a Student's t distribution with n-2 d.f.  This may therefore be used as a test statistic and we reject H₀ if its absolute value exceeds the relevant critical t value. Once the estimated standard errors and  have been computed, it clearly is a simple matter to test the null hypothesis α=0 and β=0. The test statistics used,  and are referred to as t ratios. It is customary to present sample regression equations with these ratios placed in parenthesis underneath the estimates and . That is, we present

        =           +          

Example 3: 

     There are occasions when we may wish to test hypothesis other than β=0 and α=0. Suppose we wished to test the hypothesis that the parameter β takes some non-zero value β*. Under H₀:β=β* and we set the required test statistic which is  . Under H₀ a Student's t distribution with the usual n-2 degrees of freedom. For example, in a four-person household consumption function, we might wish to test whether the MPC b of households was less than unity. We can set up a null hypothesis H₀: β=1 and test it using the test statistic . Since the alternative has to be H_A: β<1, we use a lower tail test. (In the alternative hypothesis we set β<1 because in this case b represents MPC, and as we know its value varies from 0 to 1, something which implies that b cannot take a value greater than 1). Under H0, the test statistic has a Student's t distribution, so we expect its value to be close to zero. Since we will reject H₀ if the OLS estimate  is sufficiently different from unity, we reject if the test statistic is sufficiently different from 0. Given an one-tail test and taking the 0.05 level of significance, with n-2 d.f, the relevant critical value is t= 1.714. We reject H₀ if the absolute value (or calculated value) of the test statistic exceeds this value. We suppose that for our sample we know that  and . 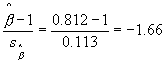Hence, the test statistic takes a value   .Since the absolute value of the test statistic does not in this case exceed the critical t value, we cannot reject the null hypothesis β=1. So we must conclude that on the bases of the present sample, there is not enough evidence to say that the MPC of households is less than unity.  

Copyright © 2002                                                                             Back to top

Evgenia Vogiatzi                                                                    <<Previous  Next>>