Sistemas de representación de cuaternios

Representando cuaternios

Es difícil conceptualizar a los cuaternios, porque de entrada no es sencillo entender a los números complejos. Podemos empezar por recordar la definición de i, en base a lo que sabemos de números imaginarios.

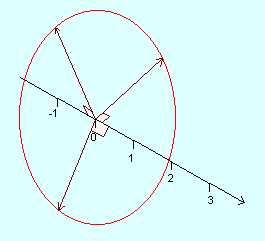
Para empezar, i es un número tal que su cuadrado es -1, debido a que esto no es posible para ningún valor en la recta de los números reales, se representa a i, como un punto situado a una distancia de 1 del origen, pero en una dirección perpendicular a la recta de los reales.

Ahora imaginemos la misma recta de los reales, pero flotando en el espacio. Existe toda una circunferencia de puntos alrededor del origen que cumplen con la definición de i, pues su distancia al origen es 1, y todos el plano de la circunferencia es perpendicular a la recta real.

De hecho, cualquier punto de esa circunferencia roja es una unidad imaginaria, y por lo tanto debe cumplir con la definición de i; pero por simplicidad, definamos una dirección arbitraria en ese plano, y por convención nombremos a esa unidad imaginaria en particular i. Ahora, consideremos otra unidad imaginaria perpendicular a la anterior y a la recta real, y llamémosla j. Tenemos entonces que cualquier punto de esa circunferencia es expresable en función de su componente en i y su componente en j.

Si multiplicamos i por j obtenemos la tercer unidad imaginaria de Hamilton, que es perpendicular a las dos anteriores y a la recta real, por lo tanto queda fuera de nuestro espacio. Pero si nos damos cuenta, dado que estamos tratando con espacios de 4 dimensiones, nos conviene dejar esa cuarta dimensión para los números reales, y visualizar el 3-espacio que forman i, j y k.

Existe una esfera de valores xi + yi + zi, tales que su distancia al origen es 1, según lo que dijimos anteriormente, cualquiera de esos puntos define a una unidad imaginaria válida.

Consideremos al número u = 0.6i + 0.8j, si nos damos cuenta, la magnitud de u es 1, por lo que esperaríamos que al elevar al cuadrado a u, se comporte como cualquier otra unidad imaginaria. Veamos ...

u*u = (0.6i + 0.8j)(0.6i + 0.8j) = 0.36ii + 0.48ij + 0.64jj + 0.48ji = - 0.36 + 0.48k - 0.64 - 0.48k = -1

WOW, entonces, si tomamos en cuenta a aquellos números de la forma a + bu, obtenemos que sus propiedades son idénticas a la de los complejos que conocemos, puesto que en esencia, u no es diferente a i CON RESPECTO a los reales.

También aquí se aprecia una de las razones por las que fue necesario definir que ij = k, pero ji = -k. La anticonmutatividad es necesaria para asegurar que cualquier número imaginario puro elevado al cuadrado de como resultado un real.

De hecho, creo que estaría bien adelantar la tabla de multiplicación de los cuaternios, aunque hay una sección dedicada a la multiplicación:

La manera tradicional de representar a los cuaternios es directamente como la suma de sus componentes independientes:

Q = w+ xi + yj + zk

Sabemos que w es la parte real, y el resto es la parte imaginaria (sólo que a diferencia de los complejos, la parte imaginaria es un vector de 3D, no un escalar). Podemos representar a ese mismo número Q, con la forma w + sû, donde s es la magnitud del vector imaginario, y û es el vector unitario en la dirección de xi + yj + zk.

Tenemos entonces que:

Así, por ejemplo, consideremos al cuaternio Q = - 21 + 3i + 12j + 4k, la magnitud de su parte imaginaria es igual a
, por lo tanto, es representable como:

La ventaja de esta notación, es que podemos compactar el vector unitario imaginario como û, y de esta forma, el número -21 + 13û, se comporta igual que el complejo - 21 + 13i, y tiene las mismas propiedades ante los logaritmos, funciones triginométricas, etc.

Lo que no se puede olvidar es que û, tiene un valor que le asignamos para este cuaternio en particular. Si la operación que vamos a realizar involucra 2 cuaternios, en general, sus vectores unitarios imaginarios no tienen por qué ser iguales. Un error terrible sería hacer lo siguiente:

(3 + 6i + 8j)(- 21 + 3i + 12j + 4k) = (3 + 10û)(- 21 + 13û) = - 193 - 171û ?????

¿Y cuánto vale û en la expresión de arriba?

Para cada cuaternio, el valor de û es distinto. Lo correcto sería entonces emplear dos vectores unitarios diferentes: û y ê por ejemplo:

(3 + 6i + 8j)(- 21 + 3i + 12j + 4k) = (3 + 10û)(- 21 + 13ê) = - 63 + 39ê - 210û + 130ûê

Aquí ya no fue tan conveniente hacer la sustitución, y en general el reducir a los cuaternios a la forma w + sû, es más práctico en el caso de operadores unitarios como la raíz cuadrada, el logaritimo, la exponenciación o funciones trigonométricas. Sin embargo, en la sección de multiplicación aparecen unas fórmulas que aprovechan las definiciones de producto punto y producto cruz para simplificar las operaciones.

Por el momento, para no quedarnos con el resultado pendiente, veamos que ûê es aproximadamente igual a -0.8769 + 0.2462i - 0.1846j + 0.3692k. (Si no es inmediato ver porqué, se puede verificar usando la tabla de multiplicación que aparece más arriba).

Una tercera forma de representar a los cuaternios, es prácticamente la misma que la anterior, sólo que en lugar de utilizar vectores unitarios, consideramos a la parte imaginaria en su totalidad como un vector V, el cual equivaldría a sû.

Con esta convención, los cuaternios tienen la forma (w, V), donde V es un vector de tres dimensiones. La ventaja de esta notación es que si estamos familiarizados con el álgebra vectorial, es más sencillo entender cuaternios como la suma de un escalar y un vector, el cual sería la parte imaginaria.

Por último, la forma más elaborada de representar a los cuaternios es la polar.

Recordemos primero que los números complejos podemos representarlos polarmente:

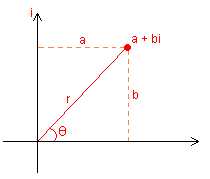
De esta forma, un complejo a + bi, está definido por su magnitud r, y por el ángulo q que forma con la recta real positiva.

Un cuaternio estaría entonces definido por su magnitud, y por tres ángulos.

La magnitud es además la definición de valor absoluto, así que al referirnos al módulo, valor absoluto o magnitud de un cuaternio Q, estamos hablando de la misma cantidad, que simbolizamos |Q|, y que está dada por:

Para entender de dónde salen los ángulos, imaginemos que sólo tenemos la parte imaginaria xi + yj + zk, y que ésta equivale al punto (x, y, z) en el espacio. Entonces, este punto puede representarse en coordenadas polares, en la forma (s, f, y). Hamilton eligió medir el ángulo acimutal desde el eje X en lugar del Z como se acostumbra:

Tenemos entonces:

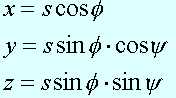
Sin embargo, esta es la parte más difícil de visualizar. El espacio completo que acabamos de considerar es un hiperplano en el 4-espacio, entonces, forma un ángulo q con la recta de los reales, de manera similar a lo que ocurre con los complejos ordinarios.

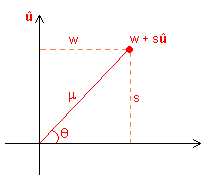
Esto equivale a:

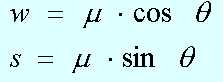
Entonces, los cuatro componentes del cuaternio quedan así:

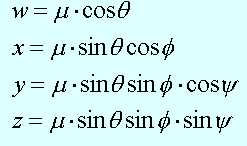
Finalmente, me gustaría mencionar otra manera algo diferente de definir a los cuaternios. Si estamos familiarizados con el concepto de tensores, entonces sabemos que tanto los escalares como los vectores están definidos como tensores de rango 0 y 1 respectivamente.

Sabemos que el producto tensorial implica un aumento en el número de dimensiones del resultado. El autor de esta página considera que los cuaternios pueden entenderse como el producto tensorial de un escalar y un vector de 3 dimensiones.