Multiplicación (2/3)
El producto de Grassman es la forma típica de multiplicar cuaternios,
pero en términos de utilidad, hay una variante que ha demostrado ser
útil para los físicos. Supongamos que queremos multiplicar A por
B, y en lugar de eso, efectuamos el producto de A* por B. (Donde A* es el conjugado
de A).
Esta evaluación, es una definición de producto, que a pesar de
que la estoy planteando en función de un producto de Grassman y una conjugación,
es una operación independiente y no secundaria.
Hubiera sido igual de válido plantear las reglas de este producto, y definir al producto de Grassman en función de éste, y de una conjugación.
Producto de Euclides
Este producto que a primera vista parece ser una complicación, se llama Producto de Euclides, y tampoco es conmutativo. Además, hay una gran desventaja, pues a diferencia del Producto de Grassman, el de Euclides no es asociativo, pero como veremos en la siguiente sección, por lo general no se toma al producto euclídeo completo, sino sólo una parte.
Para simbolizar el producto de Grassman, empleamos la simple yuxtaposición, o el * como símbolo de multiplicación. Con el objetivo de evitar confusiones con los símbolos de los productos vectoriales, los dos puntos (:) representarán el producto euclídeo.
La tabla de multiplicación quedaría entonces:
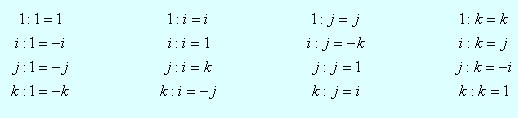
Dado que los números reales cumplen con que R = conj(R), entonces a*b = a:b si a y b son reales, por lo que los dos productos difieren únicamente cuando hay unidades imaginarias involucradas.
Pero para el producto de Euclides, los imaginarios NO conmutan con los reales.
La forma más sencilla de evaluar un producto Euclidiano, es simplemente conjugar el primer multiplicando, y luego efectuarlo como cualquier otro porducto de Grassman. Ejemplo:
| (2 - j + 5k) : (i - 8j + 3k) | = | (2 + j - 5k)(i - 8j + 3k) |
| = | 2i - 16j + 6k + ji - 8jj +3jk - 5ki + 40kj - 15kk | |
| = | 2i - 16j + 6k - k + 8 + 3i - 5j - 40i + 15 | |
| = | 23 - 35i - 21j + 5k |
Nuevamente, existe una fórmula directa para la multiplicación:

Para la forma compacta, basta con recordar que (a, b, c, d):(e, f, g, h) = (a, -b, -c, -d)(e, f, g, h)
![]()
Si queremos la forma, vectorial, simplemente, partimos de que (w, V) : (w', V') = (w, -V)(w', V'), y aplicamos directamente la fórmula que ya teníamos y obtenemos:

Copyright © 1999-2001 Ricardo Arturo Espinoza Reyes