Quantum nonlocality
The quantum framework is in some respects deeper than spacetime - the information flows which are deployed by the framework are difficult to characterize in spacetime terms.
"Before the measurement there is no particle pair; there is only a gigantic atom. This atom pervades all space. The experiment dematerializes the atom, and in its place two particles appear. Each materializes, as it must in the universe, so as to preserve the laws of nature."
Marvin Chester,Primer of Quantum Mechanics
Generally, physical systems have global properties which continue to evolve globally even as the system becomes spatially separated - when the "parts" of the system are measured then they will manifest correlations which embody (or "cash in") the previous global state. Might these correlations be the result of local processes, perhaps involving other, unknown or "hidden" facts about nature? No. (This is precisely what John Bell proved, in 1964.)
The process generating the correlations is "nonlocal".
Can it be used for signalling then? No.Given quantum theory signalling via the quantum process is not in the cards...
·Yet quantum theory is an idealization, and some have shown how relaxing aspects of the idealization uncovers nonlocal possibilities.
·More fundamentally, we are nonlocal by virtue of simply being. What happens in the universe, and in our selves, is very different than would happen in a locally bound, classicalesque world.
The history of nonlocality
Einstein, Podolsky and Rosen first focused attention on correlated, spatially extended quantum systems in 1935, though in their argument they assumed 'locality' in order to find fault with quantum theory. 25 years later Bell's result showed that EPR's assumption was mistaken. In 1989, Greenberger, Horne and Zeilinger sharpened Bell's results further by considering correlated states with 3 or more entangled particles.
|
EPR |
|
Bell's theorem |
|
GHZ |
|
Mermin |
There is a relation between the kind of entangled states considered in these proofs and the phenomenon of quantum computation.
How deep does it go?
The full extent of nonlocality as a physical fact is not well understood - for example, does a superfluid exhibit nonlocality? Generally, almost any "collapse of a wavefunction" appears to be nonlocal: is this an artifact of our description?
Since the 1964 analysis of John Bell (Bell's theorem) it is widely recognized that in some sense the nonlocality is real - quantum mechanics is a much different theory than one could assemble with local parts. In the words of Henry Stapp (1977),
"The present formulation asserts that a theory entails a nonlocal connection if there is no conceivable way for the results in each region to be independent of the choice made in the other region. Quantum theory has such a nonlocal connection: That is what Bell actually discovered."
It is probably not possible to signal using quantum nonlocality, though in my view it is a complete mistake to conclude from this that all of the nonlocality "washes out" in practice. (In fact it does not wash out!)
One could turn the question around by viewing the quantum description as completely global, and ask what is the root of the apparent, provisional locality.
What is at the root of nonlocality?
"That the guiding wave, in the general case, propagates not in ordinary three-space but in multidimensional-configuration space is the origin of the notorious 'nonlocality' of quantum mechanics..."
John Bell
Speakable and unspeakable
in quantum mechanics
Einstein, Podolsky and Rosen
EPR discussed such systems as a way of critiquing what they called the completeness (as opposed to the correctness) of the quantum description. In 1964 John Bell used David Bohm's version of EPR's argument to ironically rule against them: EPR's assumption of locality is found to be false, releasing quantum theory from any claim of incompleteness or inconsistency.
The status of nonlocality in quantum mechanics is still being debated.

EPR's starting point and central idea is that we can measure some aspect of one of the pair and subsequently predict outcomes of measuring corresponding aspects of the second one.

EPR said that since this property of the second particle was predictable after the first measurement, it was therefore "real." (EPR suggested that the particle's properties were like the inevitably mismatched socks of Bell's colleague Bertlemann: once you see one of Dr. Bertlemann's socks you could make predictions about the other consistent with the fact that the socks are real
.)
The counterfactual idea: But for that matter, EPR argued, we might just as well instead measure some other, perhaps contradictory (complimentary) property of the first particle, and in this case we would know some corresponding other fact about the second particle in the pair: this 'other' property of the second particle would be "real."
The assumption of locality: We at first go nowhere near the second particle (which might be at the other end of the galaxy by this time): we are only measuring the first particle to start with - EPR said that surely we could not alter "the real situation" of the second, distant particle, by measuring the first...
EPR said, since
Yet in the case of complementary variables quantum theory denies that both properties can be simultaneously present.
EPR concluded that since there were "real" properties of the world not even defineable in quantum theory, quantum theory is "incomplete."
The line of argument initiated by EPR was formally updated in 1964 when John Bell showed that the assumption of locality made by Einstein, Podolsky and Rosen was itself actually in contradiction with facts predicted by quantum mechanics.
The quantum properties are not like Bertlemann's socks after all.
(Eventually these nonlocal "predictions" were experimentally verified.)
Bell summed it up this way in 1964,
The paradox of Einstein, Podolsky, and Rosen was advanced as an argument that quantum mechanics could not be a complete theory but should be supplemented by additional variables. These additional variables were to restore to the theory causality and locality... That idea will be formulated mathematically and shown to be incompatible with the statistical predictions of quantum mechanics.
Bell's theorem
Bell inverted the EPR argument since EPR had used locality as an assumption - Bell's theorem converted EPR's local-realist position into a paradigm of what is not true.
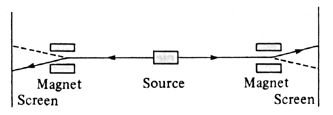
Bell's ingenious proof focused on EPResque 2-particle systems: pairs which are perfectly correlated along any given measurement axis - recall that EPR had taken this correlation as implying underlying variables, but Bell problematized this conclusion by examining some other similar correlations of the pairs: for example when measured along respective axes with a relative rotation though some angle...
With a relative angle between them the correlation between the two measurements is no longer perfect but varies as the cosine of the angle. Bell explored the type of underlying variable models (with built in locality) which EPR had suggested, and showed that the entire class of such models could in this case not give the same cosine varying correlation as quantum theory predicted.
Generally, the quantum correlations are "stronger" than the limit possible for local hidden variable theories.
In 1991 GHZ sharpened Bell's result by considering systems of three or more particles and deriving an outright contradiction among EPR's assumptions.
Quantum theory "looks" nonlocal (e.g. I measure here and collapse everywhere) and Bell's theorem seems to resolve the question in the affirmative. In the language of wavefunction collapse, Bell-GHZ showed that wavefunctions "collapse at a distance" as surely as they do locally.
The GHZ nonlocality proof
In 1991, GHZ fundamentally updated Bell's result, essentially by investigating Bell-like relationships in correlated systems of more than two particles. What they showed surpassed Bell's result by eliminating the statistical nature of the proof.
They show a situation involving three particles where after measuring two of the three, the third becomes an actual test contrasting between locality and the quantum picture: a local theory predicts one value is inevitable for the third particle, while quantum mechanics absolutely predicts a diffent value. (So, we only have to run the experiment once.)
This is really equivalent to older proofs about the modeling of the quantum state by underlying variables, as was pointed out by David Mermin - Kochen and Specher required over a hundred particles in their original proof, while GHZ have it down to three.
The Aharonov-Bohm Effect
"AB showed that one of the results of elementary quantum theory is that there are physical effects on charged particles in regions in which the electromagnetic field is nonexistant. The controversial features of the AB effect concern its interpretation; there is no disagreement as to the effect itself. The interpretation problem arises because the charge particles are influenced although they always move in field free regions. Hence the key question of the AB effect concerns localization and action-at-a-distance. AB claimed a special significance for the electromagnetic potentials because they are non-zero 'where the action is,' whereas the fields are zero in the regions to which the charged particles are confined."
Quantum coherence
There are several distinct but very closely interrelated uses of the term "coherence" in physics. For example,
·Pure states' are coherent
·Many-particle states may exhibit macrosopic quantum coherence
·Classical coherence is also important
The first two of these share in common that a quantum wavefunction informs the evolution of a physical system as a whole, perhaps nonlocally. The second two have in common that given systems exhibit patterning, so that information about one part of a system provides information about other parts.
"A quantum coherent state thus maximizes both global cohesion and also local freedom! Nature presents us with a deep riddle that compels us to accomodate seemingly polar opposites..."
Mae-Wan Ho,The Rainbow and the Worm
Coherence is important to the physics of nonlocality,
computation,
biology,
and cosmology.
Pure States
For example, the fundamental picture of a particle in quantum mechanics is that all of the alternative possibilities open to the system co-exist as a 'superposition' in a 'pure state' which is said to be coherent. (The process which converts a pure to a mixed state is known as 'decoherence'.) In this sense one can say of the two-particle singlet state considered by EPR and Bell that
"The two particles are, as it were, entangled with each other in a pure or coherent state." (Ho, 1993)
cf. Mandel's "Coherence and indistinguishability"
Macroscopic Quantum Coherence
A second, intimately related form of coherence involves multiple particles that that share a quantum state which is governed by a macroscopic wavefunction - this typically has the name 'quantum coherence', and typically involves the spaciotemporal organization of the multiparticle system. (This is closely related to what is called 'Bose-Einstein condensation'.)
"What is quantum coherence? This refers to circumstances when large numbers of particles can collectively cooperate in a single quantum state..."
Roger Penrose
Examples of quantum coherence in many particle, macroscopic systems include superfluidity, superconductivity, and the laser.
Of these three paradigm systems, the former two (superfluidity and superconductivity) are basically equilibrium systems, whereas the the laser is our first example of an open system which achieves coherence by energetic pumping - this latter idea is of the greatest importance for understanding the general implications of coherence. The laser functions in thermal environments (eg. room temperature) and there are are other, perhaps many other, nonequilibrium possibilities for coherence to exist and endure at macroscopic and thermally challenging scales, as for example, Frohlich has shown...
Classical Coherence
When systems undergo phase transitions (e.g. boiling) they may become ordered ...