CAPITULO 3

ANTEPROYECTO DE CARRETERAS

3.1. - GENERALIDADES.

Después de haber hecho en la etapa de estudio del trazado un reconocimiento en el campo de cada una de las rutas seleccionadas, y luego de hacer una evaluación de cada una de las alternativas y seleccionar la que reúna mejores condiciones llegamos a la etapa del anteproyecto donde se debe fijar en los planos la línea que represente la ruta seleccionada y para tal fin hay que realizar un estudio topográfico de la misma a través de una poligonal base.

3.2. - POLIGONAL BASE.

La poligonal base recibe este nombre debido a que servirá de apoyo para el futuro replanteo de la obra.

El levantamiento de esta poligonal consiste en la medición de los ángulos y los lados, en la nivelación de todos sus vértices y en la toma de las secciones transversales.

Estas poligonales son abiertas, por que comienzan y terminan en puntos diferentes, pero deben tener controles en su trayectoria, según esto se pueden presentar dos casos:

a) Poligonales que comienzan y terminan en puntos de coordenadas conocidas, las cuales tendrán control azimutal y métrico.

b) Poligonales que comienzan y terminan en puntos de coordenadas desconocidas, las cuales tendrán control azimutal a través de acimutes determinados por medio de observaciones solares y que se aconsejan realizar cada 5 kilómetros.

Los instrumentos utilizados en el levantamiento de esta poligonal deben garantizar la precisión exigida, los mismos deben ser tales como teodolitos, niveles automáticos, cinta métricas, estadía invar, etc.

3.2.1. - DETERMINACIÓN DEL AZIMUT DE UNA LINEA POR EL METODO DE OBSERVACIÓN SOLAR.

3.2.1.1. - DEFINICIÓN.

El acimut de una línea, es el ángulo diedro formado por el plano meridiano que pasa por el lugar del observador (A), y un plano que contiene la vertical del lugar y la línea que se desea orientar.

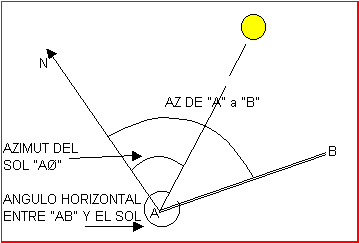
En la figura:

AB: Línea que se desea orientar.

A: Ubicación del observador.

B: Señal, el otro punto que define la línea que se desea orientar

AN: Dirección norte, traza del plano del meridiano local que pasa por el observador "A".

AØ: Acimut del Sol

AZ_A^B : Acimut de la línea AB

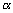: Angulo horizontal entre la línea que desea orientar (AB), y la visual al Sol.
Este método usado para determinar el acimut de una línea por altura del sol constituye el más comúnmente aplicado en trabajos de topografía, y él consiste en hacer una serie de punterías o bisecciones al Sol y a la señal.

3.2.1.2. - DATOS Y REQUISITOS NECESARIOS PARA LA OBSERVACIÓN SOLAR.

Se deben presentar los siguientes datos:
1. - Hora y fecha de observación.
2. - Distancia Cenital o altura del Sol.
3. - Declinación del Sol.
4. - Angulo horizontal entre la línea a orientar y el Sol.
5. - Latitud y Longitud de la estación, la cual puede ser tomada directamente de una carta geográfica, o bien, determinada expeditivamente con el Sol en el transcurso de la observación misma, u obtenida a través de la utilización del Sistema de Posicionamiénto Global o GPS.
6. - Temperatura.
7. - Presión atmosférica.
8. - Estado del cronómetro.
9. - Las observaciones deben ser limitadas entre los treinta (30°) y sesenta (60°) grados de distancia cenital, lo cual ocurre generalmente entre las 8.00 horas hasta 10.00 horas y desde las 14.5 horas hasta las 16.5 horas.

3.2.1.3. - FORMULISMO BASICO.
Con la altura media obtenida, la latitud de la estación y la declinación del Sol en el instante correspondiente al término medio en el tiempo, el triángulo de posición resultará fácil de resolver, y poder obtener así el acimut del Sol para el momento considerado.
Este acimut solar obtenido, combinado con el ángulo horizontal medido, proporciona el acimut deseado.

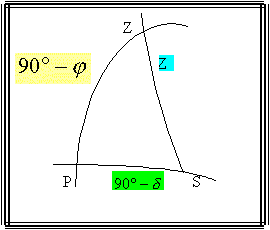
Del triángulo de posición PZS de la figura y aplicando el teorema del coseno al lado PS, obtenemos:

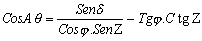
Donde:

A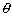 : Acimut del Sol.
: Declinación del Sol.
Z: Distancia cenital.
: Latitud de la estación.

3.2.1.4. - PROCEDIMIENTO DE CAMPO.
1. - Centralización y verticalización del instrumento sobre la estación "A".
2. - Colocación de una señal (jalón, estadia. mireta, ficha, etc.), en la estación "B".
3. - En la estación "A", visualizando a "B" con el instrumento, colocación de la lectura acimutal cerca de 00° 00´ 00", lectura y anotación del ángulo de salida. (Se supone ya preparada la libreta de campo); lectura y anotación del Rumbo Magnético de la línea "AB"; lectura y anotación de la Presión Barométrica y la Temperatura.
4. - Colocación de vidrios ahumados (acodados, etc.), en el anteojo para observar el sol. (Posición Directa).
5. - Visualización del Sol por anteojo (los hilos del retículo deben estar completamente nítidos, al igual que la imagen del Sol. Existen varios métodos entre los cuales uno de los más utilizados es el método de la tangencia. Si se usa el método de la tangencia a los bordes del Sol, se puede usar cualquier par de cuadrantes opuestos, pero se recomienda el esquema ilustrado en la figura:

Como regla general se puede adoptar que: Los cuadrantes opuestos al movimiento del Sol se tomarán para hacer la tangencia a los bordes del mismo.
Se usarán las voces características en Astronomía, como un acuerdo entre el observador y el anotador, para una mejor coincidencia entre la tangencia al Sol, tomada por el observador y la hora tomada por el anotador.
Estas voces son: ¡ preparado.....listo.....tic !

6. - Lectura y anotación (inmediatamente) de la hora (en hora, minutos y segundos): luego lectura y anotación de los ángulos horizontal y vertical (antes se hace la coincidencia del micrómetro y se cala el nivel del circulo vertical).

7. - Apunte de nuevo al Sol y se siguen los pasos 5 y 6. Para una mejor precisión en la determinación del acimut, se recomienda, un intervalo de un minuto entre dos series en distintas posiciones del anteojo, (como intervalos máximos se pueden aceptar dos y tres minutos respectivamente). Se tomarán en esta posición directa tres punterías, para luego invertir la posición del anteojo.

8. - Se continúa el proceso hasta completar tres punterías en posición inversa.

9. - Luego, en esta posición inversa y quitando el vidrio ahumado del anteojo, se observa a la señal sobre la estación "B", Completando así una serie con los datos suficientes para el cálculo del acimut de una línea.

3.2.1.5. - MINUTA DE CAMPO.
Las anotaciones en la libreta de campo, se deben realizar de la manera más amplia posible, y siguiendo una misma forma acorde a las exigencias del organismo interesado. La siguiente figura, muestra la forma indicada de llevar una libreta de campo:

3.2.1.6. - CALCULO Y REDUCCIÓN DE LAS OBSERVACIONES.
Una vez obtenidos los datos de campo, ellos deben ser verificados antes de proceder a calcular el acimut solar.
Esta verificación se realiza mediante el ploteo sobre una cuadrícula de los valores de H y V contra el tiempo, t, donde H y V representan los ángulos horizontales y verticales respectivamente y t, los correspondientes tiempos de la observación. De estos gráficos pueden determinarse las distintas correcciones que debidas a errores groseros pudieron presentarse en las observaciones y las cuales debemos corregir.
Del ploteo obtenemos 4 rectas:
I) Horizontal - tiempo; posición directa.
II) Horizontal - tiempo; posición inversa.
III) Vertical - tiempo; posición directa.
IV)Vertical - tiempo; posición inversa

Las rectas I, II, III y IV deben ser paralelas entre sí. (ver ejemplo).
Una vez que se han ploteado H y V contra t y efectuadas las correcciones a que hubiere lugar, pasamos a efectuar los cálculos que se precisan para una observación solar, a saber:
Cálculo de la hora.
Cálculo de la distancia cenital.
Cálculo del ángulo horizontal.
Cálculo de la declinación del Sol.

CÁLCULO DE LA HORA:
De la minuta de observación se toma el promedio de las horas. Este valor debe ser corregido por el estado del cronómetro.
A la hora corregida se le suma la longitud del lugar para obtener finalmente la hora en GREENWICH correspondiente al instante de la observación. Este valor será luego empleado en el cálculo de la declinación del Sol, conviene para los cálculos posteriores, expresar en decimales la hora obtenida.

CÁLCULO DE LA DISTANCIA CENITAL:
Sea Zp, el promedio de los ángulos leídos, se hallará un valor Z, corregido por refracción y paralaje, aplicando la siguiente expresión Z = Zp + R - P. Donde R es la corrección por refracción y P es la corrección por paralaje.

CÁLCULO DEL ÁNGULO HORIZONTAL:
Sea Hp el ángulo horizontal promedio entre la línea a orientar y el Sol y sea Ho la dirección promedio dirigida a la señal "B". El ángulo horizontal definitivo "H" se obtiene según la siguiente expresión: H = Hp - Ho

CÁLCULO DE LA DECLINACIÓN DEL SOL:
Las efemérides traen este valor tabulado para las 0 horas de tiempo universal, y además la variación por hora. (Actualmente existen programas de computarizados que determinan este valor).
Para conocer la declinación del Sol, en el instante de la observación, se corrige el valor de la declinación que trae la efeméride, por el valor que se obtiene al multiplicar el número de horas transcurridas desde las 0 horas de tiempo universal, hasta el instante de observación, por el factor de variación por hora de la declinación.

3.2.1.6.1. - CORRECCIONES.
3.2.1.6.1.1. -CORECCIÓN POR PARALAJE:

El triángulo esférico astronómico que resolvemos respecto a "Z", acimut, tiene su centro en el centro de la tierra.
Pero nosotros estacionamos en "A" en la superficie de la Tierra la Distancia Cenital medida deberá reducirse para obtener la Distancia Cenital correcta, que se medirá estando el observador situado en el centro de la Tierra.

Luego la corrección por paralaje (P") viene dada por la expresión:

P" = 8.75",Sen Z´ P en segundos sexagesimales

Z´: Distancia cenital medida.

3.2.1.6.1.2. -CORECCIÓN POR REFRACCIÓN ASTRONOMICA.
El aire, como todas las materias que sienten la atracción de la gravedad, es pesado, y ese peso produce como es sabido la presión atmosférica, que en circunstancias normales, queda equilibrada por una columna de mercurio de 760 mm. de altura resultando por ésta razón tanto más denso cuando más cerca esta de la superficie de la Tierra, es decir, que las densidades varían inversamente proporcional a la altura, a mayor altura sobre la superficie de la Tierra, menor será la densidad de las capas atmosféricas, se supone además que la densidad es la misma en cada capa concéntrica y que su aumento varia gradualmente de arriba abajo.
Esta propiedad hace que un rayo de luz proveniente de un astro cualquiera, antes de llegar al observador, sufre una desviación en su trayectoria (según la Ley de Snell) lo cual hace observar el objeto no sobre la dirección del mismo, sino sobre la tangente de la "Curva de Refracción"

En la figura esta representada (con deliberada exageración) la superficie de la Tierra y las capas concéntricas de la atmósfera conforme va aumentando la densidad.

Tomando en consideración de que hasta los 75° de distancia cenital se puede despreciar la curvatura terrestre y por ende las capas atmosféricas se suponen planas y no esféricas, y por aplicación sucesiva de la Ley de Snell resulta la siguiente expresión para él calculo de la corrección por refracción para la distancia cenital:

R" = 60.2TgZo R en segundos sexagesimales

Zo: Distancia Cenital medida.

En la practica, las condiciones atmosféricas varían muy frecuentemente, lo cual obliga a tomar la presión y la temperatura ambiente al comienzo, intermedio y al final de las observaciones, con lo que la expresión anterior se transforma en la siguiente:

P: Presión atmosférica promedio expresada en centímetros de columna de mercurio.
T: Temperatura promedio expresada en grados Kelvin (°K)

El valor R esta tabulado en:
a)Solar Ephemerides and Surveying instruments Manual.
b)The Star almanac for Land Surveyors.

3.2.1.7. -EJEMPLO DE CALCULO.
Se presenta a continuación un ejemplo de calculo de observación solar, utilizando la planilla elaborada en La Universidad del Zulia, Venezuela, para tal fin.

Dicha observación fue utilizada en Maracaibo, el día 29 de mayo de 1.975.
Estación teodolito: LUZ II
Estación visada: LUZ III
Instrumento utilizado: WILT T-2
Latitud de la estación: 10° 40´30".
Temperatura: 32°C
Presión Barométrica: 76 cms de hg.

3.3. - PRECISIÓN DE LOS LEVANTAMIENTOS TOPOGRAFICOS.
En Venezuela, de acuerdo a las especificaciones Generales para Estudios de Carreteras para la poligonal base, las siguientes son las tolerancias permitidas, propias de una poligonal de tercer orden.
Medidas horizontales:

Error de cierre lineal no mayor de: metros

Terreno ondulado: 0.025 metros

Siendo L la longitud de la línea en metros.

Angulos horizontales:

Desviación máxima de los rumbos astronómicos: 30"

Tolerancia entre rumbos astronómicos observados y calculados: 30"

segundos. Siendo "n" él numero de vértices.

3.4. -DIBUJO DE LOS PLANOS DE LA FAJA DE ESTUDIO.
Con los datos de la poligonal de precisión se van a confeccionar los planos de conjunto, plantas, perfil longitudinal y secciones transversales.
El plano de conjunto, dibujado generalmente a escala 1:25000 ó 1:10000, permite obtener la disposición adecuada de las láminas de planta sobre las cuales va a elaborarse el anteproyecto. De esta manera, dentro de cada lámina deberá quedar dispuesta la mayor longitud posible de la poligonal.

3.4.1. - DIBUJO DE LA PLANTA.
El dibujo de la planta se hace generalmente en láminas o en rollos de papel transparente de 50 a 55 cms. de ancho y tan largos como sea posible usándose la escala 1:1000, aunque en terrenos francamente llanos también se puede emplear la escala 1:2000.
En estos planos debe aparecer la poligonal base dibujada a escala, con los siguientes datos: Número de cada vértice, ángulo en cada vértice y coordenadas de cada vértice.
Igualmente deben indicarse en líneas finas, pero visibles, las secciones transversales con sus acotamientos respectivos, las curvas de nivel dibujadas de 2 en 2 metros en zonas montañosas y onduladas, y de metro en metro en zonas llanas, destacando las curvas correspondientes a las cotas que son múltiplo de diez.
En cada plano debe señalarse el norte astronómico y una cuadrícula de coordenadas

3.4.2. - DIBUJO DE PERFIL LONGITUDINAL.
Este se hace en papel milimetrado, en escalas 1:1000 horizontal y 1:100 vertical, o 1:2000 horizontal y 1:200 vertical. Esta relación de escala facilita la visualización de los datos del perfil.
En estos planos se dibujará el perfil natural del terreno deducido de las curvas de nivel de la planimetría, indicando todos los detalles importantes de la topografía del terreno, quiebres del mismo, quebradas, ríos, rumbos obligados, etc.

3.4.3. -DIBUJO DE LAS SECCIONES TRANSVERSALES.
Los datos de las secciones transversales se utilizan para dibujar el perfil del terreno, en dirección transversal a la poligonal base, y para dibujar las curvas de nivel en el plano de planta.
Para el dibujo de los perfiles transversales se usan las escalas 1:100 ó 1:200.
En la lámina de papel milimetrado se señala un eje vertical y para cada sección se marca un datum. Los datos de la sección transversal son dibujados a derecha e izquierda del eje.

Ing. Jesús Ordóñez