THERMODYNAMICS
Basic Definitions
:
System:
It is a definite quantity of matter of
fixed mass and identity bounded by a closed surface. All things other than
the system is surroundings ( Both space and matter ). There are three
types of systems.
- Closed system - There is no mass transfer between the system and surroundings. But their is energy transfer. E.g.. compression of a gas in a piston cylinder.
- Open system - Both mass and energy transfer takes place. It is classified into steady and unsteady flows. Eg. Turbine
- Isolated system - No mass and no energy transfer takes place. E.g. All subsystem of a power producing system
All things other than the system that are outside the wall that interact with the system in question is called as surroundings. There are different types of walls that are used to separate the system from the surroundings. They are rigid wall, diathermal wall and adiabatic walls. A rigid wall does not permit the volume of the system to change. A diathermal wall is one that will make it possible for the system to communicate thermally with its surroundings. Two systems separated with a diathermal wall is said to be in thermal contact. An adiabatic wall is the one that is impermeable to thermal energy. Such a wall cuts of the thermal interaction between between a system and surroundings.
Properties:
Properties are used to identify the state of the system and
solely dependent upon the state of system and not upon how the state was
reached. A quantity is a property if it has a exact differential. A
quantity can be called a property of the system if the changes in the value
between two equilibrium states of system is same. Properties may be
directly observable or indirectly observable characteristic of a system.
Two properties, namely the temperature and entropy are unique to
thermodynamics. There are two types of
properties. They are
- Extensive state properties: Here the value of entire system is equal to sum of the values of the parts of the system. They are dependent upon the mass. E.g.. Total Volume, total energy
- Intensive state properties: The value of the entire system is not equal to the sum of the parts of the system. These properties are not dependent upon the mass. E.g.. Temperature, pressure, Density etc.
Path and point functions
: 
This is with reference to a system being taken from state 1 to 2. There may be any three quasi static process A, B, and C. Area below the curve gives the amount of work involved in each case.
Thus the value of work depends upon the path and not on the end state of the process. Hence work ( and also heat ) are path functions. On the contrary thermodynamic property are point functions. These are definite values for a given state. The change in property is independent of the path and depends on only the initial and final states ( Exact differential )
Process:
Whenever a system undergoes a change, process is
said to have taken place. There are different types of process. They
are
- Reversible process: Is the one in which both the system and surroundings return to their original state. All real time process are irreversible. Process are irreversible due to turbulence, temperature gradient and Friction. In a reversible process there should be no viscous force or coulomb friction in the system
- Cyclic Process: The end states are identical. The system undergoes a series of change and returns to original condition.
- Quasi-static Process: The system departs from the equilibrium condition only infinitesimally.
- Adiabatic Process : There is no heat flow between the system and surroundings. ( ∆ = 0 )
Work and Heat:
Work is the energy in transition in which the energy flows from the system to
the
surroundings.
Heat is the energy in transition which flows from one body to another body on
account of the temperature difference between the two
bodies. Unit of heat is Joule
Both the Heat and work are Transient Phenomena, Boundary Phenomena and Path
functions.
Derivation for displacement work:
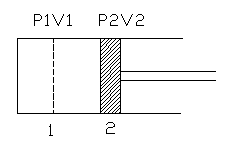
This derivation is valid only for quasi static process. Consider a cylinder of area 'a' and length of the piston is 'l'. The piston moves due to gas pressure. Between section 1 and 2, the value of pressure and volume is P and V. When the piston moves the force acting on the piston is
F = pressure x area = P.a
Work done = Force x distance moved = F.dl = P.a.dl
We know that area x length = volume. Hence a.dl = v. Thus the above equation for work done becomes P.v. Thus when a piston moves from 1 to 2 the amount of work done is given by dw = ∫ Pdv
Internal energy:
A system undergoes a change of state in which both heat transfer
and work transfer are involve. The net energy accumulated is stored in the
system. It is denoted by the symbol U, it includes all form of energy
other than kinetic and potential energy.
Q - Heat
to the system.
W -
Work from the system.
( Q - W ) is the net energy stored in the system.
This ( Q - W ) is
neither heat or work and is given the name, internal energy of system. The internal energy is just a form of energy like the potential
energy of an object at some height above the earth, or the kinetic energy of an
object in motion. In the same way that potential energy can be converted to
kinetic energy while conserving the total energy of the system, the internal
energy of a thermodynamic system can be converted to either kinetic or potential
energy. Like potential energy, the internal energy can be stored in the
system.
Entropy:
Entropy means transformation. It increases with the addition of heat and
vice versa. Change in entropy can be defined. Over a small range the
increase or decrease in entropy when multiplied with absolute temperature, gives
the heat absorbed or heat rejected. For any reversible process, the change
in Entropy of system and surroundings is Zero.
Entropy is the index of unavailability of energy.
Energy that goes down the sink is less available for any useful work.
Entropy changes are accompanied by heat transfers. But may also take place
with out the transfer of heat. In a reversible process, if the entropy of
the system increases, then the entropy of surroundings decreases by a equal
amount. Entropy is a property like T and V.
Change in entropy of a system along two equilibrium states
can be obtained by taking the system along any reversible path connecting the
states, dividing the heat added at each point with the temperature
and summing the quotients.
Energy:
It is the capacity to produce effect. There are two
types of energy. They are stored energy ( E.g.. Potential energy, Kinetic
energy and Internal energy ) and Transient energy ( Heat, work and electric
energy ).
Power:
The rate
of energy transfer is called as power. The unit is watts. 1 W = 1
J/s = 1 Nm/s
Throttling
:
The fluid
expands from high pressure to low pressure without doing any work. There
is no change in KE and PE. Hence there is no heat transfer.
Nozzles and Diffusers:
Nozzles increases the
kinetic energy of flowing fluid by creating a pressure drop. But in
diffusers, the pressure is increased and Kinetic energy is
decreased.
Carnot's
Cycle:
It is a
reversible cycle in which the ideal gas receives heat at one temperature and
rejects heat at another temperature. There are 2 isothermal and 2
reversible adiabatic process. Efficiency of carnots cycle is given by
η = W / Qa = ( Qa - Qr ) / Qa
Enthalpy:
Of a substance
is defined as the sum of internal energy and flow work. h = u +
pv.
Graham's Law of Diffusion of Gas:
It states that
the rate of diffusion of a gas is inversely proportional to square root of
density.
Zeroth Law of Thermodynamics:
If two bodies are in equilibrium with a third body, then the two bodies are in equilibrium with each other. Through this concept, the temperature of the system may be measured by bringing it into thermal equilibrium with a thermometer. Following the conversion factors between various temperatures.
R = F + 459.67
K = C + 273.15
K = 1.8 R
First Law of Thermodynamics:
This law deals with
conservation of energy, which states that energy can neither be created not
destroyed, but can be changed from one form to another.
Whenever a system under goes a cyclic change the
algebraic sum of work transfer is proportional to the algebraic sum of heat
transfer. Work and heat are inter convertible.
First law could be said as law of internal
energy. However the drawback in this law is that it does not tell anything
about direction of heat flow.
Second Law of
Thermodynamics:
For an isolated system, only those processes can take place for which the
entropy of the system increases or remains constant. Second law could be called as law of entropy.
In this there are two statements.
Lord Kelvin and Max Planck's statement of the Second Law: It is impossible to construct a device operating in a cycle for the sole purpose of extracting heat from a reservoir and changing it into an equal amount of work without rejecting a part of the heat. i.e. it is impossible to devise a machine that converts 100% of heat into work. i.e. The universe is cooling down.
Clausius' statement
of the Second Law: It is impossible to construct a device that operating in
a cycle will produce no effect other than the transfer of heat from a cooler to
a hotter body. The spontaneous flow of heat from a colder body to a hotter body
is impossible.
Third Law of Thermodynamics:
It introduces the
concept of absolute entropy. It states that the total entropy of pure
substances approaches 0o as the absolute temperature approaches
0o. ( It is impossible to reach the absolute zero of
temperature in any physical process. )
Thermodynamic Equilibrium:
When a collection of matter experiences no more changes in all its properties, then it is in a state of thermodynamic equilibrium. But a real system is never in equilibrium. To attain thermodynamic equilibrium, Mechanical, Chemical and Thermal equilibrium should first be obtained. When a system has no unbalanced force within it and when the force its exerts on its boundary is balanced by external force, the system is said to be in Mechanical equilibrium. When the temperature of the system is uniform throughout and is equal to the temperature of the surroundings, the system is said to be in thermal equilibrium. When the chemical composition of a system will remain unchanged, the system is said to be in chemical equilibrium.
Thermodynamic reservoirs:
There are three different types of thermodynamic reservoirs. They are work reservoir, heat reservoir and Matter reservoir.
Work reservoir:
It is a device that we may employ to keep track of the amount of work done by or done to a given thermodynamic system. It is a body in which every unit of energy crossing the boundary is work energy. A work reservoir might be visualized as a perfectly elastic spring that is compressed by the work done on it by a system, or as a weight that is raised as the system does work upon the reservoir and lowered as the reservoir does not work on the system.
Heat reservoir:
It serves as a heat source or heat sink, in the analysis of thermodynamic problems. It can be considered as a body with large energy capacity so that its temperature remains constant when heat flows into or out of it. The atmosphere around the earth and the ocean may be considered as heat reservoirs.
Matter reservoir:
Matter, as well as heat and work can cross the boundary of an open system, the surroundings of an open system may be imagined to contain only heat and work reservoirs but also one or more matter reservoirs to supply and receive matter. A matter reservoir is considered to be sufficiently larger than the system so that the reservoir itself remains in a given equilibrium state. The atmosphere around the earth may be considered as a matter reservoir supplying air to the engines of our automobiles and to air separation plants.
Important Thermodynamic Process:
The below mentioned process uses the concept of DU = Q - W
| Process | Significance / Example | Implications | Pictorial Representation |
| Isobaric Process | Pressure
is Constant (DP
= 0)
Gas heated in a cylinder fitted with a movable frictionless piston. The pressure the atmosphere and the pressure due to the weight of the piston remains constant as the gas heats up and expands. |
DU is zero in a constant pressure process. For an ideal gas, constant pressure work is W = Ú PdV = PDV Heat that flows into the system causes the temperature to rise. Q = m Cp DT = mR( T2 - T1 ) |
 |
| Isothermal Process | Temperature is constant
(DT = 0)
The gas in a cylinder is compressed slowly enough that heat flows out of the gas at the same rate at which is being done on the gas. |
For an Ideal gas U is
a function of the temperature, Hence DU is zero since DT = 0. Since DU = 0 then W = Q.
P1V1 = P2V2 = nRT, for an isothermal process. Work done W = PV ln( V2/V1 ) which is also the equation for Q. |
 |
| Isochoric process | Volume is constant (DV = 0)
Heating of a gas in a rigid, closed container. |
No work is done on the gas
because W = Ú PdV = Ú
P ( 0 ) = 0. This implies that DU = Q = m Cv DT.
V1 = V2 = nRT1/P1 = nRT2/P2, the ideal gas law for constant volume process. |
 |
| Adiabatic process | No heat flows into or out of
the system ( Q = 0 )
Compression of a Gas in an Insulated Cylinder. |
DU = W ( Since Q = 0 ). Hence any
temperature rise or fall is due to the work done or by the gas alone.
W = (P1V1 - P2V2) / (g - 1) |
 |
| Isentropic process ( Rev. Adiabatic process ) | Entropy is constant ( DS = 0)
A heat engine in which the working fluid undergoes an adiabatic reversible cyclic process. |
Any isentropic process is
also adiabatic since DU = Ú dQ/T and Q = 0. However, not all
adiabatic process are isentropic.
For a reversible heat engine, not only the change in entropy of the working fluid must be zero but also DU of the environment (heat reservoirs) must also be zero. |
 |
| Polytropic process | PVn is
constant
Compression or Expansion of
a gas in a real system such as a Turbine. |
n = 0 for Isobaric
process since PV0= P = constant. n = 1 for Isothermal process since PV1 = PV = NKT = constant. n = 0 for Isovolumetric process and n = g for Adiabatic process. |
 |
Specific Heat:
It is the heat required to raise the temperature of
unit mass of substance by one degree. There are two types, they are
specific heat at constant volume ( Cv )and Specific heat at constant pressure (
Cp ). Its unit is J/Kg/K
For air Cp = 0.24
J/Kg/K and Cv = 0.171 J/Kg/K
The ratio of Cp /
Cv = Gamma. and Cp - Cv = R / j
Gas Laws:
There are 5 gas laws. All perfect gases obey all gas laws under all conditions of pressure and temperature.
-
Boyle's law : At constant temperature PV = C. The magnitude of C depends upon the volume of the gas.
-
Charles lay : At constant pressure V α T.
-
Gay - Lussac law : At constant volume P α T.
-
Joules law : Change of internal energy is directly proportional to the change in temperature.
-
Avagadro law : Equal volumes of all gases under the same pressure and temperature contain equal number of molecules.
|
Ideal Gas |
Real
Gas |
|
Obeys the equation of state at all conditions of pressure and temperature. |
Obeys the equation of state at all conditions of Pressure and temperature, except at the point where Pressure approaches absolute Zero. |
|
The gases cannot be liquefied or
solidified |
Can be solidified and
liquefied. |
|
Specific heat values are
constant |
Not so, Varies with temperature and pressure. |
Ideal gas equation : PV = mRT where
P is in N / m2 V is in m3 T is in K R is gas constant in Nm / Kg oK
Following are the assumptions for a ideal gas
-
Molecules occupy a negligible volume fraction.
-
Long range forces of attraction between the particles are negligible.
Assumptions of Kinetic Theory
-
Large number of molecules ~ their motion can be treated statistically.
-
Molecules are in continuous and rapid motion which is random, colliding with each other and the walls of the vessel very frequently, the collision being elastic.
-
Pressure originates from the summation of large number of reacting forces as the molecules bounce off the walls.
Combustion chamber:
Combustion Chambers convert the chemical energy stored in a liquid or gaseous fuel to an enthalpy increase in the gas passing through them. Usually, the gas is air, but it could be any gas with the proper components to react with the fuel. A combustion chamber requires one initial spark to begin the combustion of the fuel in the chamber. After that, the chamber will function as long as it has fresh fuel and gas. The fuel combusts, or burns, in the chamber. This combustion releases large amounts of energy to be absorbed by the gas. This increases the temperature and enthalpy of the gas.
REFERENCES:
1. Engineering Thermodynamics, Francis F. Huang.
2. Engineering Thermodynamics, P. K. Nag.