Parametric Equations of the Ellipse

Differentiating with respect to the Eccentric Angle
|
R = Semi-Axis lying on the x-axis
r = Semi-Axis lying on the y-axis Differentiating with respect to f dy/df = d(r · sinf)/df = r · cosf dx/df = d(R · cosf)/df = R · (– sinf) |



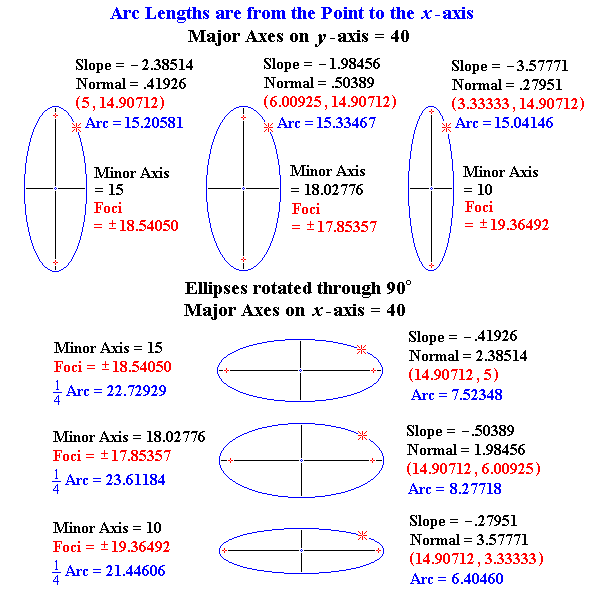
Simpson's Rule : Estimating the Arc Length of an Ellipse
|
Given any two stations x1 > x2
Semi-Axis lying on the x-axis = R Semi-Axis lying on the y-axis = r Parametric Angle at x1 : f1 = arccos (x1 ÷ R) Parametric Angle at x2 : f2 = arccos (x2 ÷ R) The interval between the angles is divided into twenty equal strips : Δf = (f2 – f1) ÷ 2 , where f2 > f1 The values of y are determined : y1 = Square Root [(R sin f1)2 + (r cos f1)2] Angle f1 is incremented by Δf : y2 = Square Root [(R sin (f1 + Δf))2 + (r cos (f1 + Δf))2] For each successive value of y, angle f1 is incremented again by Δf : y3 = Square Root [(R sin (f1 + 2 × Δf))2 + (r cos (f1 + 2 × Δf))2] y4 = Square Root [(R sin (f1 + 3 × Δf))2 + (r cos (f1 + 3 × Δf))2] ... other terms ... y21 = Square Root [(R sin (f1 + 20 × Δf))2 + (r cos (f1 + 20 × Δf))2] The values of y are multiplied and summed as per Simpson's Rule : Ellipse Arc Length = (Δf ÷ 3) × (y1 + 4y2 + 2y3 + 4y2 + 2y5 + ... + 2y19 + 4y20 + y21) |