Sierpinski's Gasket

Brief Explaination:

Area Calculations:

Start with any triangle, and include its interior. Create an inner triangle by connecting the mid-points of the original triangle's sides, and remove the inner triangle's interior. Do the same to each of the 3 remaining triangles, removing their inner triangles' interiors. Do the same to each of the 9 remaining triangles, removing their inner triangles' interiors. Continue this process. Notice that with each step, the area is reduced to 3/4 of the previous step's area. So, as n increases without bound, the area decreases and approaches zero. Sierpinski's gasket is the limit toward which the geometrical structure gets closer and closer.

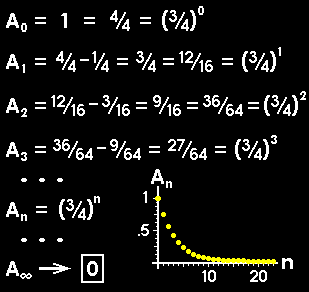First Published:  June 10, 2003
By:  xStatProf   | Home | Email |