LA TRANSFORMACIÓN DE LAPLACE
1.0. Definición:
Supongamos una función f(t): de R en R en principio de cuadrado integrable en el intervalo 0, oo.
Definimos la transformación de Laplace de f (t) y la denotamos como F(s) como:
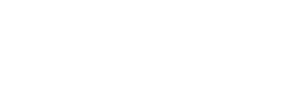
Notemos que la transformación en cuestión asocia a cada función del espacio de funciones considerado otra función F(s) con parámetro s.
La utilidad de esta transformación se verá patente cuando se expongan sus propiedades.
Notese que no todas las funciones tienen una transformada de Laplace: Podemos encontrar funciones que al intentar calcular su transformada de Laplace nos de lugar a una integral no convergente para cualquier valor de s. Las funciones que tienen transformada de Laplace bien definida en algún intervalo de s las llamaremos funciones admisibles por dicha transformación en dicho intervalo. Así mismo al margen de valores de s en el cual la transformada de Laplace puede ser evaluada se le llamará dominio de la función transformada.
Una condición necesaria para que una función sea admisible para algún intervalo es que su ritmo de crecimiento sea inferior al de una exponencial en t:
2.0. Transformación de Laplace de algunas funciones.
En este apartado ilustraré la transformación de Laplace aplicada a varias funciones de uso corriente en el analisis de circuitos: