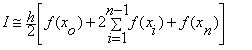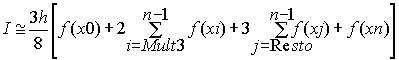Con frecuencia surge la necesidad de evaluar la integral definida de una función que no tiene una antiderivada explícita o cuya antiderivada tiene valores que no son fácilmente obtenibles. el método básico involucrado para aproximar cualquier función a su integras se conoce como cuadratura 
numérica y se usa una sumatoria de las función evaluada en un intervalo. Los métodos de integración numérica se pueden utilizar para integrar funciones dadas, ya sea mediante una tabla o en forma analítica. Incluso en el caso en que sea posible la integración analítica, la integración numérica puede ahorra tiempo y esfuerzo si sólo se desea conocer el valor numérico de la integral.

Los métodos de integración numérica se obtienen al integrar los polinomios de interpolación. Por consiguiente, las distintas fórmulas de interpolación darán por resultado distintos métodos de integración numérica. Los métodos que se estudiarán se refieren a las fórmulas de Newton-Cotes, que se basan en las fórmulas de interpolación con puntos de separación constantes y se deducen de integrar las fórmulas de interpolación de Newton, así como la fórmula de interpolación de Lagrange. A su vez, las fórmulas de Newton-Cotes se subdividen en las de tipo cerrado y las de tipo 
abierto. Las reglas del trapecio y las dos reglas de Simpson pertenecen al tipo cerrado.
 

Regla del trapecio:

Esta regla es un método de integración numérica que se obtiene al integrar el polinomio de interpolación de primer grado (Lineal). Para obtener una buena precisión se necesita un gran número de subintervalos.

Esta regla se basa en la interpolación polinomial cuadrática (de segundo orden). Obteniendo el polinomio de Newton ajustado a tres puntos  e integrando el resultado se tiene la regla de 1/3 de Simpson. El número de intervalos utilizados en esta regla debe ser par. (N=par).

Esta regla de 3/8 se obtiene al integrar una formula de interpolación de tercer grado. Para la regla extendida se aplica a un número de intervalos que sea múltiplo de tres.
 

Cuando el número de intervalos es impar pero sin ser múltiplo de tres, se puede utilizar la regla de 3/8  para los primeros tres o los últimos tres intervalos y luego usar la regla de 1/3 para los intervalos restantes, que son un número par. Puesto que el orden del error de la regla de 3/8 es el mismo 
que el de la de 1/3, no se gana mayor exactitud que con la regla de 1/3 cuando uno puede elegir con libertad entre ambas reglas.).