
Gamma Power Densities
This paper addresses a generalization of the gamma densities. This generalization encompasses many other distributions as special cases. In addition to providing a more general parametric distribution, it serves to model some nonstationary distributions.
1. Gamma Power Densities
Consider a variable x having a gamma density function (1). That is, the following density function.
pun(x) = mn/G(n) xn-1e-mx x>0, n>0
The distribution function can be computed for integer n.
Pun(x) = 1 - e-mx ( Sr=0..n-1 (mx)n-r-1/G(n-r) ) x>0, n>0
This distribution is not readily invertable for median or percentiles but can be solved numerically. If we then consider the density of x(1/a), then the resulting function is
paun(f-1(x)) df-1(x)/dx = amn/G(n) xan-1e-mxa x>0, n>0
The distribution function becomes (for integer n)
Paun(f-1(x)) = 1 - e-mxa ( Sr=0..n-1 (mxa)n-r-1/G(n-r) ) x>0, n>0
This family of densities concentrated on [0,¥), together with the symmetrized densities on (-¥,¥),
psaun(x) = paun(|x|)/2 n>0
encompass many of the most common continuous probability distributions. Some of these are enumerated in the following table. Note that the Weibull family of distributions (2) can be considered the distribution of an exponentially distributed variable raised to a power.
a m n Probability Distribution
1 m n Gamma of mn
a m 1 Exponential power or Weibull of am
1 m 1 Exponential of m
2 m 1 Rayleigh of m
a m 1/2 Normal power of am
2 m 1/2 Half normal
-1 >m 1/2 Positive stable index 1/2
Symmetrized Probability Distribution
1 m 1 Bilateral exponential
2 m 1/2 Normal
These relations can be illuminated by locating these densities in amn space. The scale parameter m can be neglected. Graphing the locations of the densities in the an plane, we find for a¹0, n>0, m>0

2. Moments
Computing the moments about the origin, using the substitution y = mxa, dy = amx(a-1) dx, we find
mn = ò x=0..¥ xnpamn(x)dx x>0, n>0
= amn/G(n) òx=0..¥ xan+n-1e-mxa dx
= 1/(mn/aG(n)) òy=0..¥ yn+n/a-1e-y dy
= G(n+n/a)/(mn/aG(n))
For n=0, m0=1, thus these are indeed probability distributions. The first few central moments derived from these are below. An arbitrary distribution may be fit using these moments.
n nth Central Moment
0 1
1 G(n+1/a) / m1/aG(n)
2 (G(n+2/a)G(n)-G2(n+1/a)) / m2/aG2(n)
3 (G(n+3/a)G2(n) - 3G(n+2/a)G(n+1/a)G(n) + 4G3(n+1/a)) /
(G(n+2/a)G(n)-G2(n+1/a))3/2
Some of the limits are useful in describing the general behavior. As n®0, the distribution approaches a kernel at the origin, while for a®¥, the distribution approaches a kernel at unity. For n®¥, or a®0, the moments diverge.
3. Modes
Taking the derivative of the density with respect to x and setting it to zero, we find
dpamn(x)/dx = amn/G(n) xan-2e-mxa(an-1-axa) = 0
x = (n-1/a)(1/a)
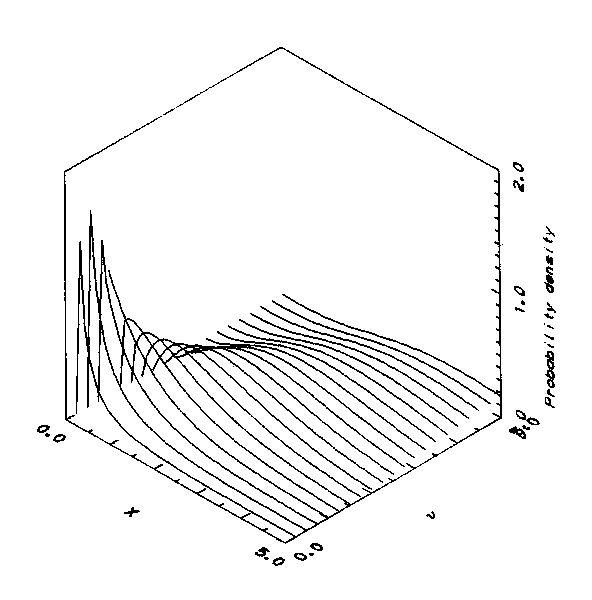
For n£1/a, the mode occurs at 0. For n<1/a, the density diverges at 0, while for n=1/a, the density is amn/G(n) at 0. For n>1/a, the density is 0 at 0. The density as x®¥ always approaches 0. Some graphs showing parametric variations for the case of m=1 are included. Functions divergent at 0 have been set to 0.
Gamma Densities for For n=1.

Gamma Densities for a=1.
4. Sums, Products, and Ratios
While the family of gamma densities is closed under convolution, this is not true of gamma power densities in general. Thus a sum of random variables following a gamma power distribution is not gamma power distributed in general. Forming the mixture product and ratio distributions, X*Y and X/Y, we find neither of these is gamma power distributed. Therefore, while these densities may be of use in nonstationary processes or descriptive statistics, they are limited in other respects.
5. References
1. An Introduction to Probability Theory and Its Applications, Volume II, Second Edition, William Feller (Wiley, 1971), II.2, page 47.
2. Automatic Detection Theory, D. C. Schleher Ed.