New web site: www.petar-bosnic-petrus.com
ANTIGRAVITY or GRAVIFUGAL FORCE
and GRAVIFUGAL FLYING CRAFT Scientific paper PACS 03 02 + i (Classical physics)
CONTENTS
PART I Definition of the Gravifugal Force
Centripetal and Centrifugal Forces
Centripetal, Axipetal, and Axilongal Forces
Specific Features of the Rotating Mass of Celestial Bodies
Vectorial Analysis of a Rotating Mass at the Geographical Latitude j = 45o
a) First Group of Facts -- Values of the Gravifugal and Gravipetal Forces
b) Second Group of Facts -- Relative Value of the Gravipetal Force
c) Third Group of Facts -- the Value of the Axilongal Force F axl List and equations of forces
Double-Curved Trajectory of the Ring Mass (The first key part of the theory)
Experimental Proofs (The second key part of the theory)
Application of the Presented Principles on the rotation of ring of the Gravifugal Flying Craft
Behaviour of gravifugal Flying Craft and Its Accordance with Energy Conservation Law PART II Small, Experimental Gravifugal Flying Craft
Attention
LARGE gravifugal Flying Craft fitted with Rings that are Permanent Magnets
Gravifugal flying Craft fitted with quantum ring
PART I
Definition of the Gravifugal Force
Dear visitor, sorry having to say: antigravity does not exist. Fortunately, instead of it, there is, a gravifugal force. This force is real, experimentally proved, and something much better and much more suitable and useful than so called antigravity.
When speaking about the gravifugal force we in fact refer to a certain sort of centrifugal force created by rotation in which gravity acts as centripetal (i.e.gravipetal) force . Direction of the gravifugal force is always opposite to that of the gravipetal (gravity).This concept of gravifugal force is based on Newton's understanding of gravity as an attracting force, on the law of action and reaction, and the law of inertia, and has been deduced from them by means of the mathematical tools provided by the Huygens' theory of the centrifugal force.
Centripetal and Centrifugal Forces
Designations ?centripetal? and ?centrifugal? do not denominate any special forces, but rather directions in which a particular force acts during a rotational process -- towards the centre or away from it, or rather, towards the axis of rotation or away from it. Any of the known forces may be centripetal in direction, that is to say, perform the function of the centripetal force.
The following table lists all centripetal and centrifugal forces
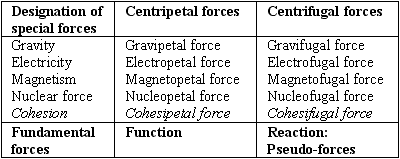
The above table clearly shows that the function of the centripetal force is performed by fundamental forces, with the exception of the cohesive force; hence its slight separation from the others. This force also can be called solidity, and consequently , in a case of rotation , solidopetal and solidofugal force.
Centripetal, Axipetal, and Axilongal Forces
In regard to the direction of action it is also important to differentiate between axipetal and centripetal forces. Axipetal force is directed toward the axis of rotation, and the centripetal toward the gravity centre of the rotating celestial body.
Particularly, I want to draw attention to the axilongal force - the one acting along the axis of rotation. This force can be caused exclusively by the rotation of a celestial body, or by the rotation of a disc or ring within a gravitational field.
Specific Features of the Rotating Mass of Celestial Bodies
First and foremost, it must be pointed out that the cohesipetal force - soliditity - which enables a solid body to rotate without being dispersed is not a fundamental force but an inertial, pseudo-force. Differences in the after-effects of rotation of solid body (with regard to the rotation of a celestial body) result from the fact that rotation of celestial bodies is made possible by the fundamental, gravipetal force. It is of utmost importance.
Let us observe Figures 1a and 1b which show forces that result from the rotation of a steel sphere ( 1a ) and the forces created by the rotation of a spherical celestial body (1b). Lines of the cohesipetal force resulted from the rotation of a steel sphere are perpendicular to the rotation axis and at the same time are parallel to one another, and since they are directed toward the rotation axis they are designated as lines of the axipetal force. Lines of the gravipetal force are directed to a single point in the centre of a celestial body, while the gravifugal force F gf spreads radially from that point -- the point of application of force.
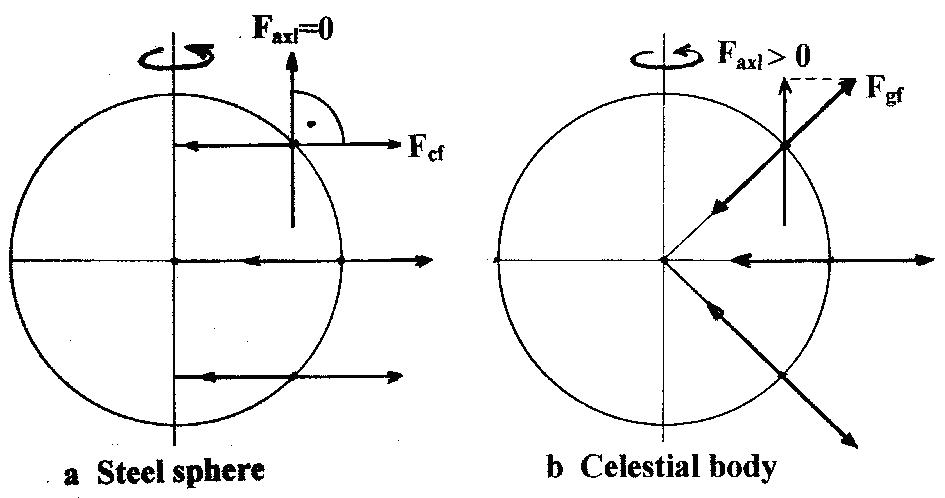
Figure 1 a and 1 b
In the case of the steel sphere , force F axl (axilongal force), active in the direction that is parallel to the rotation axis, will equal zero for two independent reasons:
1.In accordance with the laws of symmetry, the force directed upward from the plane of rotation equals the force directed downward so consequently, the two cancel each other out.
2.We can arrive at the value of the force parallel to the rotation axis by multiplying either the cohesifugal or the cohesipetal force by cos90 o , which equals zero. Bearing in mind that 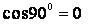 , the force parallel to the rotation axis, i.e. the force active in the direction, F axl , will equal zero regardless of the velocity at which a ring or some other mass may rotate. , the force parallel to the rotation axis, i.e. the force active in the direction, F axl , will equal zero regardless of the velocity at which a ring or some other mass may rotate.
However, the very fact that gravipetal and gravifugal forces (Fig. 1b) spread in a different manner from cohesipetal and cohesifugal forces (Fig.1a) indicates that where the rotation of a celestial body is concerned, the axilongal force, F axl could exceed zero value. This in turn means that the concept of the gravifugal flying craft is not a pointless one, since the rotation of a ring rotating in the vicinity of some celestial body would create the axilongal force, F axl the value of which would be proportional to the rotation velocity, v of the ring.
Vectorial Analysis of a Rotating Mass at the Geographical Latitude j = 45o
a) First Group of Facts -- Values of the Gravifugal and Gravipetal Forces
Rotation of the mass of a celestial body at its equator is determined by only one force: gravipetal force, F gp , while rotation at latitudes greater than zero requires an additional force: cohesipetal force F cp (Fig. 2). This force is always perpendicular to the direction of both the gravipetal and gravifugal forces. Its function is to maintain the observed mass on a parallel the radius of which is smaller than the radius of its equator. Cohesipetal force, F cp is in fact a mechanical tension (tension of the solid body material) directed toward a designated point on the rotation axis of celestial body which is, in fact, the point of application of the cohesipetal force.
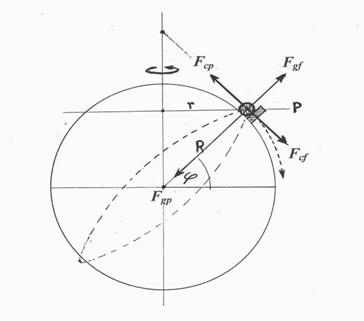
Figure 2
If there were no cohesipetal force, an observer standing on Earth (and rotating with it) would notice that the observed mass is accelerating toward the equator, i.e. in the direction of the cohesifugal force F cf . This potential trajectory is marked by the curved dotted line culminating in an arrowhead. The component known as the ?horizontal component of geocentrifugal, (i. e. of geoaxifugal) force? is in fact nothing more than the cohesifugal force F cf . To a stationary observer in space recording the trajectory of the observed mass this trajectory would appear to be circular -- designated as an ellipse (dotted line) in Fig. 2.
(The cohesipetal force appearing in connection with rotating celestial bodies is ultimately a derivative of the gravitational force. This can be observed directly in rotating gaseous bodies, i.e. those without solid crust. However, this is neither the place nor the time to go into a detailed explanation of this phenomenon.)
The expression for the value of the gravifugal force is: 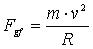 , and for , and for
the value of cohesifugal force it is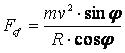
b) Second Group of Facts -- Relative Value of the Gravipetal Force
Figure 3 is a representation of rotation of the observed mass at  . Let us first assume that an observed celestial body is not rotating, in which case the only force existing there would be gravity. If that were the case, the observed mass would exert pressure on the surface of the celestial body of . Let us first assume that an observed celestial body is not rotating, in which case the only force existing there would be gravity. If that were the case, the observed mass would exert pressure on the surface of the celestial body of 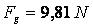 . There is no rotation and no symmetry in relation to the rotational plane P. . There is no rotation and no symmetry in relation to the rotational plane P.
Now let us assume that the linear velocity of the mass equals the velocity of satelisation: c. 7900 m/s. At that velocity and at the given geographical latitude j = 45 O all four forces determining the rotation of the observed mass -- the forces of the inner circle -- would be equal: c. 9.81 N. It is clearly visible that they are symmetrical in relation to the rotational plane, but the weight of the observed mass, or rather the pressure it exerts upon the surface of the celestial body, has fallen to zero.
Let us further assume that the rotational velocity of a celestial body could be considerably increased, and together with it the velocity of the observed mass, and let us observe the behaviour of the forces (after such increase in velocity). The outer circle represents the area of increased speed and the limit to which the observed forces have increased.

Figure 3
Our observation will tell us that the only forces to have increased would be pseudo-forces: cohesipetal, cohesifugal, and gravifugal. This is logical and, indeed, essential, since the value of these forces depends on the factor 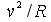 , i.e. it is proportional to velocity v and inversely proportional to the value of radius R. , i.e. it is proportional to velocity v and inversely proportional to the value of radius R.
The fourth force, gravipetal force F gp , has not increased. This is a fundamental force and its absolute value is determined by the
expression 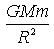 , and it existed prior to rotation, which was not the , and it existed prior to rotation, which was not the
case with the other three pseudo -forces. The relative value of the gravipetal force is inversely proportional to the rotational velocity of the celestial body, i.e. to the velocity of the observed mass. This relative value of the gravipetal force, F gp is defined by the expression
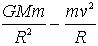 . The greater is the value of pseudo-forces or rather, . The greater is the value of pseudo-forces or rather,
the higher is the rotational velocity of a celestial body, the lower is the relative value of the gravipetal force.
At this juncture I should point out that the value of the gravifugal force cannot exceed the absolute value of the gravipetal force (gravity) since that would contradict Newton's Law of action and reaction. When the velocity of the observed mass exceeds the velocity of satelisation v s it is not the value of the gravifugal force which increases, but rather the observed mass must increase the radius R of its trajectory, i.e. the distance from the centre of the celestial body -- that is to say, from the point of application, or source of the gravipetal force. In fact, the observed mass must lift off the surface -- in other words, it starts to levitate .
The most important observation at this point is following:Gravifugal force tends to violent symmetry or equality among the forces in relation to rotational plane, P. The vector sum of the forces at the ?upper? side of the plane P tends to be greater than the sum of the forces at its ?lower? side. This means that the observed mass (in order to maintenance equality of action and reaction forces), will accelerate in the direction of the gravifugal force action, F gf . and increase the radius R of its movement. This reaction will decrease the value of gravifugal force.
The ring of the gravifugal flying craft, to be discussed later in this text, behaves in exactly the same manner.
Important differences
In a case of rotation of solid body, at which the centripetal force is performed by pseudoforce (solidity or cohesion) centripetal and centrifugal (i.e. cohesipetal and cohesifugal) forces increases itself proportionaly with velocity of rotation, up to destruction of solid body.
At the rotation of celestial body or any other rotation in which the centripetal force is performed by some foundamental force, centripetal and centrifugal forces are decreasing by enlargement of velocity of rotation, and are inversely proportional to that velocity.
At the first, this phenomena appears as a decreasing of weight of observed mass, and after acheivement of velocitiy of satelisation, as an increasing of radius R . As I just stated, this is a way of maintenance of the phenomenon of equality of action and reaction forces, described by Newtons law 2.
Decreasing of weight was proven by gravimetrical meassurement, and increasing of radius R by flight of arificial satelites.
c) Third Group of Facts -- the Value of the Axilongal Force F axl
However, vital to the requirements of the gravifugal flying craft is the value of acceleration in the direction of the axilongal force F axl . Figure 4 will assist us in determining the value of that acceleration.

Figure 4
Velocity of the observed mass is considerably greater than the velocity of satelisation.
The value of the axilongal force F axl is arrived at by multiplying the cohesipetal force F cp by cos j and the gravifugal force F gf by sin j , and then by adding the two results. From the obtained total we deduct the value of the cohesifugal force F cf , multiplied by cos j .

The value of the axilongal force is therefore proportional to the rotational velocity v, to the sinus of the angle φ, and inversely proportional to the motion radius of the observed mass R, i.e. to the distance from the centre of the celestial body.
 only in three cases: a) only in three cases: a) , b) , b) , and c) , and c)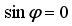 ( ( 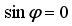 is only at the Equator). is only at the Equator).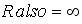 only at the equator. only at the equator.
If we want to know a velocity maintaining in equilibrium and derivative of gravitational force , we can get it by equation: . Values achieved by this equation are in quite accordance with establish knowledge and experience
Warning
In order to achieve correct understanding of this phenomenon, at this point, we must repeat once again our statement from previous chapter.
“When the velocity of the observed mass exceeds the velocity of satelisation vs, it is not the value of the axilongal force which increases, but rather the observed mass is increasing the radius R of its trajectory, i.e. the distance from the centre of the celestial body. In fact, the observed mass must lift off the surface i.e. it starts to levitate”
“It is a way of maintenance of the phenomenon of equality of action and reaction forces, described by Newtons law 2.”
List and equations of forces


Figure 5
Double-Curved Trajectory of the Ring Mass (The first key part of the theory)
In an effort to make things as simple and clear as possible, thereby making the problem easier to understand, I ask the reader to imagine a rotating ring (as shown in Figure 6) at some moderately high latitude.
If we wanted to present the motion of the ring mass through Euclidean geometry we should take into consideration, above all, the fact that every particle of the ring mass on the way from point A to point F is always at equal distance from the centre of the celestial body. It is assumed, of course, that the axis of rotation of the ring is identical, or co-axial to the direction of action of gravity. If the trajectory of the ring mass from point A to point F is projected onto a plane we shall obtain a symmetrically curved line (part of a circle) since all points are at equal distance from the centre only within a circle. From the projected trajectory it is easier to understand why the rotation of the ring must necessarily cause the gravifugal force Fgf.
By the way of clarification, during rotation of the ring its mass is continually “falling” or veering toward the centre of the celestial body (point of application of the gravipetal force). The trajectory of the ring mass is simultaneously curved toward the centre of the ring and the centre of the celestial body. The curvature toward the ring centre is visible to the naked eye, whereas the curvature toward the centre of the celestial body can be understood only on the basis of a knowledge of spherical geometry and the correct method of arriving at conclusions.
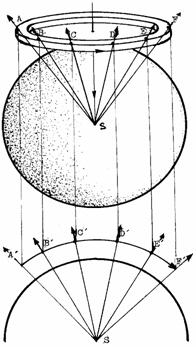 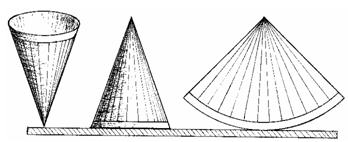
Figure 6 Figure 7
In order to make it quite clear, I would now like to give an elementary explanation of the above claims whereby the trajectory of any particle in the ring mass is not straight but curved, in other words, it veers constantly toward the centre of the celestial body. I would ask the patient reader to make a paper cone and then to draw lines on its outer surface that would extend from the base to the point (Figure 7). Now place the cone base down on a table or any flat horizontal surface. We shall see that the edge of the base touches the flat surface at all points, thus giving the impression of being as flat as the surface upon which it rests. However, when we open the mantle of the cone and spread it out we shall see that it is not flat at all, but spherical, circular (i.e. curved) and that each point on its edge is removed from the former top of the cone by the same distance.
Just as this edge veers constantly toward the former top of the cone, so do the particles of the mass of the rotating ring constantly veer toward the centre of the celestial body forming a curved, circular trajectory. It is difficult to perceive that the edge of the base is curved toward the top of the cone unless the cone mantle is opened and spread out. Similar difficulty is encountered in observing the real form of the trajectory followed by the particles of the ring mass. At first glance no one would venture to say they veer constantly toward the centre of the celestial body (say, Earth). The mass of the ring resists this veering toward the centre of the celestial body, i.e. it resists the change in direction of its motion. The consequence of this resistance, i.e. of inertia, is the gravifugal force, Fgf. The direction of its effect is marked by arrows on Figure 7.
Experimental proofs (The second key part of the theory)
Experimental proof of the existence of the gravifugal force can be found in gravimetrical tables in every text-book of geophysics. Measured values of the gravifugal force or acceleration are in absolute accordance with the values calculated on the basis of the expression 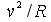 . .

Gravimeter is measuring gravifugal force too. Every point on every parallel on Earth (every geo. lat.) we can regard as point of mass of rotating ring presented at fig. 6 and 8.
Experimental proof of the existence of the axilongal force can be found in tables of navigation by gyrocompass. Every gyrocompass is provided with tables of “error of geograpfical latitude” (slight declination toward East). This “error” remains unexplained till today. I have explained it by the influence of the axilongal force. Now it is possible to calculate the “error of geographical latitude” by the following equation: 
Angle  is the value of “error”; FI is the force caused by the gyroscopical inertia (of the gyrocompass rotor). is the value of “error”; FI is the force caused by the gyroscopical inertia (of the gyrocompass rotor).
Application of the Presented Principles on the rotation of ring of the Gravifugal Flying Craft Ring
The gravifugal flying craft is a device in which a large-diameter ring rotates at high velocity. The rotation axis would always be co-axial with the direction of action of the gravitational force. See Fig. 8. The craft would lift off and levitate by means of the force resulting from the rotation of the ring, and would be active along the rotation axis. I have designated this force as the “axilongal force”. Axilongal force is, as already explained above, a derivative of the gravifugal force.

Figure 8
The ring of the gravifugal flying craft would have a radius from 1 to, for instance, 20 metres. It would be the same as if a certain mass were revolving round the polar axis at a distance of a mere 10 metres, which corresponds to the geographical latitude of j = 89.99991020. The sinus of that angle is practically 1, and on that basis the equation for the value of the axilongal force could be as follows: and for the value of the resulting force or acceleration it could be: .
At the velocity of 7900 m/s the ring of the gravifugal flying craft should levitate, and at velocities above that value it could lift a casing enclosing it. A ring of sufficient strength should be able to carry a flying craft bearing a useful load.
Behaviour of gravifugal Flying Craft and Its Accordance with Energy Conservation Law
Astronautical experience has confirmed the theory that the higher an artificial satellite flies, or rather, the greater is its distance R from the centre of the Earth, The lower must be its velocity. This is an inevitable consequence of the Law of conservation of energy: . The greater is the height h of an artificial satellite, i.e. the longer is the radius R of its orbit round the centre of the Earth, the greater is its potential energy , and consequently, the lower is its kinetic energy which is in turn lessened by the reduction in the velocity v of the satellite. Energy conservation law is also valid in case of the gravifugal flying craft.
Kinetic energy of its ring is calculated by equation and its potential energy by equation.
,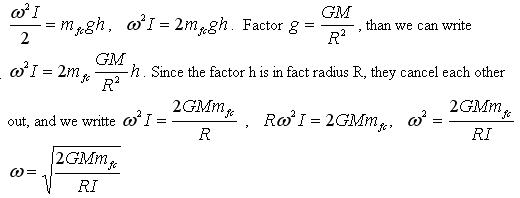
w is the angular velocity of the ring, I is the momentum of inertia of the ring, mfc is the total mass of the gravifugal flying craft, including also the ring mass, h, height is radius R i.e. distance from the centre of Earth.
The last equation clearly shows that behaviour of the gravifugal flying craft is in accordance with the energy conservation law. The larger the radius R and its potential energy, the lower is its kinetic energy i.e.angular velocity, w of its the ring.
Attention !
This is very important information.
Ring made in strehgthest non-expensive materijals of today - several kinds of carbon fiber – enables us to decrease the weihgt of ring only per max. cca 6%.
Only nano-tubes has sufficient tensile strenght power which enables gravifugal flying craft to levitate.
The strenghtest metal rings or gyroscopes are capable to decrease weight of ring or gyroscope only per cca 0, 0005 % Tensile strength of different metals are very low. Density is, unfortunately to large.
That is why no one of many scientific laboratories (dealt wiht metal gyroscopes) could not achieve considerable values in decreasing of weight of gyroscopes. They achieved cca 0,000002 % to 0,000004%. Achieved values are mainly regarded as an errors in meassurements.
By a ring made in carbon fiber is possible to achieve considerable and non-disputable values.
Nano-tubes are very expensive today. We hope its price will decrease soon. In a such case, also non-profesionals could make small gravifugal flying craft.
PART II - GRAVIFUGAL FLYING CRAFTS
Small, Experimental Gravifugal Flying Craft
Figure 9 1 is mass of the ring made by carbon fiber or nano-tubes; 2 are magnetes of permanent magnet bearing (ring or rotor); 3 magnetes of permanent magnet bearing of casing or stator; 4 aluminum mass of the ring; 5 electromagnetes made by high frequency electromagnetic core and coils – powered by 3-phase electric current;6 mass of the casing made by carbon-fiber or polyester mass.

Figure 9
Coils are powered by 3-phase electric current. They are mounted in such a way as to allow creation of a revolving magnetic field. By linking the coils into the electric circuit an opposing magnetic field is also induced in the aluminum ring mass. Due to the effect of the magnetic field the ring begins to turn in the same direction as the magnetic field of the casing. The velocity of the ring is dependent on the velocity of rotation of the casing magnetic field, while the rotation velocity of the magnetic field is dependent on the frequency of the electric power (alternating).
If you are using only minimal number of poles (9 electromagnetic poles casing, powered by 3-phase electric current), and want only to put ring (made of nano-tubes) into gravifugal levitation, you should to provide frequency of 22,2 kHz. This frequency could able ring to rotate at cca 8000m/sec and levitate. If you want just to decrease weight of ring in a value of e.g. 3%, you should provide frequency of 6kHz.
Average diameter of the ring let be 1,2m. The ring has no firm axis. It is floating in the magnetic field. The magnetic field made by permanent magnetes serves as a frictionless magnetic bearing – maglev system
If a flying craft with an aluminium ring were to be fitted with a battery of 50 Ah capacity that could feed electric energy reliably to the device for at least 2.5 hours (i.e. 9000 seconds) and if electricity from a domestic power supply were used to accelerate the ring up to the moment it is able to ensure vertical acceleration of the flying craft of only o.1 m/sec2 (in order to avoid air resistance in the lower strata of the atmosphere), and if the craft begins to use power from its own battery only after it peels away from the launching lawn, then an average acceleration of the craft at least 2.3 m/sec2, after 9000 seconds, can be relied upon. According to the formula

the flying craft will reach the distance, l of 93,150 km, which is one-quarter of the distance to the Moon. According to the formula for calculation of the ultimate speed: v = at = 2.3 x 9000 it will move away from Earth at the speed of 20,700 m/sec. If the craft is launched 60 minutes before sunrise it will travel into the endless Universe at the speed of 50,700 m/sec (including the speed of Earth -- 30,000 m/sec).
Attention
The ring becomes to decrease its weight only when its velocity exceed the linear velocity of Earth at your experimenting place, i.e. at your geographical latitude. E. g. velocity of Earth at geo. lat. 300 is cca 400m/sec. and at geo. lat. .450 is 338m/sec.
We said that every craft must be fitted by two counter-rotating rings. Among the mentioned reasons, there is still one: counter-rotating rings prevents reactive counter-rotating whole craft.
In this article there is not diagram of device with counter-rotating rings. Sorry.
Rings must have equal dimensions and equal mass, also must be accelerated by equal accelerations. The rings could be situated one under the other.
Large gravifugal Flying Craft Fitted with Rings that are Permanent Magnets
In order to demonstrate just how economical gravifugal propulsion can be, on the following pages I shall give a presentation of the construction and utilisation of a gravifugal flying craft using large permanent magnet bearings. These are, in fact, two steel magnetic rings positioned so that facing poles repel each other. The bottom, rotating, ring creates the gravifugal force while the top, stationary, ring acts as the bearing for the rotating ring. See Fig. 10

Figure 10
Fig. 10 1 - the entire rotating ring (rotor); 1a - permanent magnets used to decelerate the ring; 1b - layer of nano-tubes; 1c – metal, diamagnetic mass of the ring; 1d - permanent magnet (ring) which propels the flying craft; 2 - casing wall; 3 - evacuated casing area; 4 - stationary magnetic ring; 5 - electromagnets which accelerate and decelerate the ring; 6 - coils of electromagnets; 7 - structure of the flying craft with carbon fibre or aluminium; 8 - electric batteries; 9 - useful area.
The advantage of such a flying craft in comparison with the one described at the following pages lies in the fact that it consumes no energy when constantly hovering at any given altitude, the hovering being ensured by the remanent magnetism of the rotating and static rings, i.e. their repellent force. Should altitude be reduced, the kinetic energy of the ring rotation would be transformed back into electric energy by means of permanent magnets (1a) and coils (6) and stored in batteries. The electric energy would, of course, also be used for the horizontal acceleration and deceleration. But for horizontal movement can be used and some kind of energy, or fuel.
Bearing in mind that when hovering at any given altitude, these craft would consume no energy, they would be suitable for use as floating family homes, hotels, hospitals, industrial plants, observatories, etc. Floating platforms of this type could be positioned at any altitude above the equator, and also above the poles. Main part of future Mankind will probably live in floating cities and on floating islands.
Gravifugal flying craft fitted by quantum ring – ring made by pure light.
This type of gravifugal flying craft shown at fig. 11 was concepted long time ago, but I did not believed in its ecconomical capabilities.

fig. 11. 1 is an evacuated steel toroidal tube with inner walls as smuth as a miror. 2 is quantum ring – ring made by light. 3 Sources of the light. 4. Transparent photoelectrical elements. 5 Mass of electrical or electromagnetical device. 6 Construction made in nano-tubes. 7 perforation connecting different units od useful space. 8. Useful spaces. 9. Electrical batteries.
Theoretical posibility of this type of craft was shown by A.S. Eddington , 1919., when he tested claims of Einstein`s Theory of relativity. He confirmed Einstein`s Theory and, in same time showed that light possess an inercy. When the light is passing near the masive celestial bodies, it resist to change the direction of its movement, and change it only in a very small value.
The quantums of the light of quantum (or light) ring will behaviour in the same maner like the quantums of the ray of light and in the same manner like a particles of mass of mechanical ring. Quantums of the light of ring also will resist to the action of the gravipetal force and develop a gravifugal force. Since the velocity of light is constant, c, value of gravifugal force will depend only on the “mass” of the light ie. its quantity, q and value of the radius R – distance from the center of celestial body.
How it is functioning?
Sources of light, 3 are injecting the light into evacuated miror smooth walls toroidal tube, 1. The light, 2 is reflecting from the walls of tube and endlessly rotating through tube, without posibility to disappear. When the sufficient quantity of light, 2 is acumulated in a toroidal tube - in accordance with equation q c2/ R,
where q is in fact quantity of light - the craft starts to levitate and elevate itself .
If we want to stop elevation or levitation and let the craft down. We must put the transparent photoelectrical elements, 4 into the space of toroidal tube 1. The light will pass throhgh those transparent photoelectrical elements and transform itself into electrical energy, which can be stored into electrical batteries.
It seems to be possible the light is moving in the both directions (clockwise and counter clockwise) in the same time. Because of it there would appear interferent statical circular wave whom velocity in the same time would be 0 and c.
This craft need not to have two toroidal tubes for two counter rotating quantum rings.
I believe this type of flying craft will be suitable to fast transporting of people and goods. |
 Paranormal and UFO Directory - UFOseek.com is the largest paranormal and UFO directory.
Paranormal and UFO Directory - UFOseek.com is the largest paranormal and UFO directory.