

Instructions For Use
Introduction
The Otis King Calculator is basically a slide rule. This should
not be thought to imply that it is a particularly complicated piece of
apparatus suitable only for people with special training; the slide rule is
really a very simple article requiring no special mathematical knowledge for
its operation, yet with it the drudgery can be removed from much of the
calculating work that has to be done in industry and commerce and by students.
The Otis King is even simpler than many slide rules because it dispenses with
special purpose scales. It is also more accurate than the ordinary slide rule.
These two points recommend it to many users.
Because of the cylindrical design of the Otis King it has been possible
to produce a very compact instrument. The scales are 66 inches long and carry
many more graduations than those of an ordinary slide rule. Consequently the
user can read answers comprising several figures directly from the scales
instead of estimating the later figures; the setting of the Calculator is also
speedy since much of the counting of graduations and estimating the value of
parts of graduations is eliminated.
There are two models. MODEL K is suitable
for multiplication, division, proportion and percentages. Besides solving
these problems MODEL L gives logarithms, enabling
it to be used for working out powers and roots.
The Calculator consists of three parts, the chromium-plated holder,
the cylinder (which has a knurled top), and the cursor (engraved with two
white indicators). It will be noticed that the knurled top has a notch cut
in it. The purpose of this is to help the user to set quickly to the "1"
on the scale. The "1" is directly in line with the notch.
(Note. The outline drawings below show the correct settings of
the indicators to the scales, and should be carefully followed.)

INSTRUCTIONS
Multiplication and Division
MODEL K. This model has a scale from 1 to 10 mounted
on the holder. The cylinder also has a scale from 1 to 10
on its upper half and the same scale is repeated on the lower half.
Example: Multiply 2 by 4.
Take the holder in the left hand and open the instrument
gently to its full extent.
Set the bottom indicator to 2 — which will be found about
half an inch above the bottom ONE and slightly to the
right of it. (Remember to set to the line and the graduation, not to the figure
itself.)
Moving the cylinder by holding the knurled top, set the
middle ONE to the top indicator. The middle
ONE will be found in line with the notch on the knurled
top and about two inches below it. Do not touch the cursor when making
this movement.
Moving the cursor, slide the top indicator up to 4, which
is about one inch below the notch and a little to the right of it.
The answer 8 will be read at the bottom indicator.
Example: Multiply 4 by 4 (on Model K).
Set the bottom indicator to 4 — about one inch above the
bottom ONE and slightly to the right of it.
Move the cylinder to set the middle ONE to the top
indicator. (Remember that the cursor must not be touched during this
movement.)
Moving the cursor, slide the top indicator down to 4 on
the lower half of the cylinder scale.
The answer 16 will be read at the bottom indicator.
Example: Divide 8 by 2.
Set the bottom indicator to 8 — near the top of the scale,
about a quarter of an inch below the top ONE and a little
to the right of it.
Move the cylinder to set 2 — about 1 1/2
inches below the notch and a little to the right of it — to the top
indicator.
Moving the cursor, slide the top indicator down to
ONE at the middle of the cylinder scale.
The answer 4 will be read at the bottom indicator.
Example: Divide 16 by 4.
This is done by the same method as in the previous division example,
except that for the final movement the cursor is moved upwards to the
ONE at the very top of the scale. (For the second
movement the 4 on the lower half of the scale on Model K can be used,
instead of the 4 on the upper half of the scale; in that case the final
movement is to the middle ONE.)
MODEL L. This model has a scale from 1 to 10 mounted
on the holder. The cylinder has a similar scale on its upper
half which is used in conjunction with the holder scale for
multiplication and division. On the lower half of the cylinder
there is an evenly divided scale. This is used in conjunction
with the holder scale to find logarithms.
The instructions given for Model K, for multiplication
and division examples, also apply to Model L except where
it is otherwise indicated. They should be studied first as this
may help the user to locate the position of the numbers on the scales.
Example: Multiply 2 by 4.
Set the bottom indicator to 2.
Move the cylinder to set the 1 at the beginning of the
scale on the upper half of the cylinder, to the top indicator.
Moving the cursor, slide the top indicator up to 4.
The answer 8 will be read at the bottom indicator.
Example: Multiply 4 by 4 (on Model L).
Set the bottom indicator to 4.
Move the cylinder to set the top 1 — just below the
notch — to the top indicator.
Moving the cursor, slide the top indicator down to 4.
The answer 16 will be read at the bottom indicator.
Example: Divide 8 by 2.
Set the bottom indicator to 8.
Move the cylinder to set 2 to the top indicator.
Moving the cursor, slide the top indicator down to 1 at
the beginning of the scale on the upper half of the cylinder.
The answer 4 will be read at the bottom indicator.
Logarithms (Model L only)
The lower half of the cylinder on Model L carries an evenly divided
scale which is used for finding the logarithm of any number as follows:
Move the cursor to set the bottom indicator to 1 at the
bottom of the holder scale.
Move the cylinder to set 000 at the beginning of the
evenly divided scale to the top indicator.
Moving the cursor, slide the bottom indicator to any number on the
holder scale and read its logarithm on the evenly divided scale at the top
indicator.
(Finding antilogarithms is of course the converse of the above.
Having made the preliminary settings of the bottom indicator to 1, and 000 to
the top indicator, the top indicator is moved to the logarithm and its
antilogarithm is found at the bottom indicator.)
Understanding the Scales
To the user who is unfamiliar with slide rules, the graduation of
the scales of the Calculator may appear a little confusing, and the following
notes of explanation may be useful.
(a) No final "0"s and no decimal points are printed on the
multiplication and division scales. The user must insert these mentally, for
himself, as he requires them. Thus "57" can be used to represent "57", "570",
"57000", "5.7", ".057", etc.
(b) The value of the small graduations lying between the
larger ones against which numbers are actually marked, i.e. "101", "102",
etc., can be determined by reference to the marked numbers. Thus between
"101" and "102" the scale is marked with ten graduations and these have the
values of "1011", "1012", "1013", "1014" and so on up to "1019". If it is
desired to get a figure or to read an answer between these small graduations
the space must be divided. Thus "10115" will be set by placing the indicator
halfway between "1011" (which may of course be read "10110",
as explained above) and "1012" ("10120"). With practice the user will find
that he can judge other values such as "10112", "10116", with a fair degree of
accuracy.
(c) It will be noticed that the graduations are not of equal
value throughout the scale, and that the lower part of the scale contains many
more graduations than the upper part. Thus the scale from "1" to "2" occupies
seven turns of the spiral, from "2" to "3" occupies only about four turns,
from "3" to "4" three turns, and so on. The result of this is that at the
bottom of the scale the user can set and read numbers comprising more figures
than those to which he can set higher up the scale. Thus the graduations from
"101" to "102" are "1011", "1012", "1013", etc.; from "202" to "204" they
represent "2025", "203(0)", "2035"; and from "62" to "625" they represent
"621", "622", "623", "624". It has been shown in note (b)
how values between, say, "2025" and "2030" can be judged.
As has been explained in an earlier note, if it is desired
to read figures between, say, "202(0)" and "2025", these must be judged by the
user. For example, for "2021" the indicator mark must be set to a point
one-fifth of the distance between
"202" and "2025".
It may be helpful to the beginner if he draws the portion
of the scale on a piece of paper first, and inserts the actual
values that he requires, thus:
 (or 200, .002, etc.)
(or 200, .002, etc.)
With a little practice on these lines any person not previously experienced in
using such instruments will find that he can attain proficiency in using the
Otis King.
Further Examples
The user is advised to study the foregoing instructions first and to
attain familiarity by working through the simple examples several times. When
they have been mastered he can proceed to the following calculations. The
instructions apply to both Model K and Model L, but in the case of
Model L it may sometimes be necessary to use the bottom 1 on the cylinder
scale and on other occasions the top 1.
(For the sake of simplicity the bottom white indicator will
now be referred to as B and the top white indicator as T.)
Combined Multiplication and Division
(This type of calculation can usually best be done by alternate
multiplication and division of the individual factors, thus: 6 divide by 7,
multiply by 4, divide by 5, multiply by 9, divide by 2. There is no need to
take note of the intermediate results and except at the end of the calculation
it is not necessary to move the indicator to 1.)
| Set B to 6. Set 7 to T. Move T to 4. |
| (B now indicates answer to |
6x4
7 | )
| | |
| Set 5 to T. Move T to 9. | |
| (B now indicates answer to |
6x4x9
7x5 | ). | |
| Set 2 to T. Move T to 1. Read answer at
B: 3.086. |
Proportion
| I. | Solve 12 : 7 :: 16 : x ? |
| Set B to 12. Set 7 to T. Move B to 16. Read answer at T.
12 : 7 :: 16 : 9.333.
|
|
| II. | Solve 18 : 4 :: x : 53 ? |
| Set B to 18. Set 4 to T. Move T to 53. Read answer
at B. 18 : 4 :: 238.5 : 53. |
|
| III. | Divide 8975 in the proportions
83 : 79 : 33 : 19.
|
| Set B to 8975. Set sum of required proportion, viz.
214, to T. Move T in succession to 83, 79, 33, 19, and read the
corresponding proportions at B, viz. 3481, 3313, 1384 and 797. (On
Model L this calculation necessitates "closing in" the cylinder.
See page 9.) |
Percentages
| I. | What is
5% | (a) of 162 ? |
| (b) off 162 ? |
| (c) on 162? |
| Set B to 162 (capital amount or quantity). Set 1
to T. The instrument is now set to solve percentage problems
involving % OF, % OFF
and % ON 162. |
| (a) | Move T to 5
(rate %). Read answer at B:
5% of 162 = 8.1. |
| (b) | Move T to 95
(100–rate %). Read answer
at B: 5% off 162 = 153.9. |
| (c) | Move T to 105
(100+rate %). Read answer
at B: 5% on 162 = 170.1. |
|
| II. | What % of 3735 is
4.54 ? |
| Set B to 3735. Set 1 to T. Move B to
4.54. Read answer at T: .12155%. |
|
| III. | What is the percentage of
profit on cost where goods purchased for £5,760 are sold for
£9,420 ? |
| Set B to 5760 (capital). Set 1 to T. Move B to 9420
(selling price). Read answer at T: 163.5. Percentage of
profit = 63.5%
(163.5 – 100). |
Constant Factors
I. In cases where one pair of factors is repeated throughout a series
of problems, the instrument may be set to the constant terms, and the answers
found by subsequent movements of the cursor only.
In Percentage Example I, for instance, the
instrument being set to the constant terms 162:100%, any percentage
of, off or on 162 will be shown at B when T is moved to
the relative figure, e.g. Move T to 45. Read answer at B: 45%
of 162 = 72.9. Move T to 126. Read answer at B: 26%
on 162 = 204.1, and so on.
| II. | Decimalise 3/32, 7/32, 15/32, 29/23. |
| Set B to 32. Set 1 to T (32 and 1 being the constants
in this series). Move B in succession to 3, 7, 15, 29
and read the corresponding answers at T, viz. .09375,
.21875, .46875, .9062. |
Money Calculations
In Sterling calculations 1/2 new pence is set as 005. Thus the
setting for 22 1/2 np is 225. For
£3.01 1/2 np the setting
is 3015; do not forget the '0' in such amounts.*
| I. |
If 54 articles cost
£39.225, what is the price of 15?
Set B to 39.225. Set 54 to T. (The cost
of any number of articles at this price can now be obtained by moving
T to the number required.) Move T to 15. Read answer at B: 15 articles cost
£10.895. |
| II. | Find interest on
£675 at 6 1/2% p.a. for 29 days. |
| (£675 x |
6.5
100 |
x |
29
365 |
) |
| Set B to 675. Set 1 to T. Move T to
6.5. Set 365 to T.
Move T to 29. Read answer at B: £3.486. |
In some calculations it may be found preferable to invert the setting
of the instrument and to work to the "1"s on the holder scale instead of to
those on the cylinder scale. In this case, the answer is of course read at the
pointer opposite to the one indicated in the foregoing examples.
Model L
THE UPPER
CYLINDER SCALE. — When this
scale is used in conjunction with the Holder Scale to perform the types of
calculations described in the preceding pages, it will be noted that upon
occasion the cylinder becomes closed in or opened out too far for the pointer
on the cursor to be moved to the required figure. In this case proceed as
follows, without altering the setting of the instrument:
| | To close cylinder in. |
Move T to bottom 1.
Set top 1 to T. |
| | To open cylinder out. |
Move T to top 1.
Set bottom 1 to T. |
The pointer can then be set to the required figure and the
calculation completed. This operation may be performed during any calculation
and does not affect the process or answer in any way.
THE LOWER
CYLINDER SCALE. —
Where involved expressions occur above or below the line, the Otis King
Calculators offer valuable advantages over the ordinary slide rule, which,
even if engraved with log-log scales, cannot solve the following, whereas
Model L will give all powers and roots, fractional or otherwise, of all
numbers without limit, and solve any expression, however extended. The
following expression is given as an example:
1.0083.1 x
3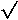 63
x 4000 63
x 4000
6 x
5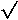 260000 x
421.82 260000 x
421.82
| = .2495. |
All involved expressions must be replaced by their numerical
value before the problem can be dealt with, and this prior process is, of
course, common to both the slide rule and the Otis King Calculator. The
intermediate stage in dealing with the above problem is to simplify it into
the following:
1.025 x 3.98 x 4000
6 x 12.11 x
900.1 |
The process for effecting this is as follows:
To LOGARIZE (i.e. find the logarithm representing a
number).
Set B to bottom 1 of holder scale. Set ".000" of
lower cylinder scale to T. Move B to number (antilogarithm), and read mantissa
at T.
To DELOGARIZE (i.e. to find the number represented by a
logarithm).
Set B to bottom 1 of holder scale. Set ".000" of lower
cylinder scale to T. Move T to mantissa. Read antilogarithm (number) at B.
To ascertain any Power or Root of any number
POWERS
Multiply the logarithm of the number by the index of
the power and take the antilogarithm of the product.
Example: What is
1.0083.1 ?
Log. of 1.008 = 0.0035.
0.0035x3.1 =
0.01085.
Antilog. of 0.01085 = 1.025.
Therefore
1.0083.1 =
1.025.
ROOTS
Divide the logarithm of the number by the index of the
root and take the antilogarithm of the quotient.
Example: What is
3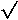 63 ?
63 ?
Log. of 63 = 1.7993.
1.7993÷3 = 0.5998.
Antilog. of 0.5998 = 3.98.
Therefore 3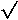 63 =
3.98.
63 =
3.98.
Compound Interest
Find the amount that £250 will become in 14 years at
5 1/2% compound interest.
| (a) | Set B to 1.
Set 000 to T.
Move B to 1055 (100+5 1/2%).
Read log. .0232 at T.
|
| (b) | Set B to 232.
Set 1 (beginning of upper cylinder scale) to T.
Move T to 14.
Read 325 at B.
|
| (c) | Set B to 1.
Set 000 to T.
Move T to .325.
Set 1 (beginning of upper cylinder scale) to T.
Move T to 25.
Read 528.5 at B. (Answer: £528 10s.) |
Approximation Method for finding Square Roots and Cube
Roots without the use of Logarithms
The following method may be used for finding approximate
square roots and cube roots on Model K:
Example: To find the cube root of 9.
Estimate it as, say, 2.
Work out 2x2x2 on the Calculator, giving 8 at bottom
indicator.
Keeping cylinder in same position, move bottom indicator
to 9. Read 225 at top indicator.
Note difference between estimate and 225 = 25; divide by
3 = 83, and add to original estimate = 2083.
Example: To find the square root of 87.
Estimate it as, say, 9.
Work out 9x9 on the Calculator, giving 81 at bottom
indicator.
Keeping cylinder in same position, move bottom indicator
to 87. Read 9665 at top indicator.
Note difference between estimate and 9665 = 665; divide
by 2 = 333, and add to original estimate = 9333.
Finding the Decimal Point
In common with all slide rules, the Otis King gives answers which do
not show the position of the decimal point. The simplest way of deciding where
the decimal point comes is by inspection and for this method it may sometimes
be helpful to make a mental calculation with approximate figures. Thus
11.03 multiplied by 20.45 gives 2257 on the
Calculator. It is roughly 10 multiplied by 20, which equals 200, so the
decimal is placed after the third
figure — 225.7.
Examples:
0.0027x0.00031 =
0.000000837;
approx. 0.003x0.0003 =
0.0000009. |
0.48x0.056 =
0.02688;
approx. 0.5x0.05 =
0.025. |
11x305x29x49 = 4761000;
approx. 10x300x30x50 = 4500000. |
577÷799 = 0.7225;
approx. 6÷8 = 0.75. |
18x19x8
1.7x0.002x950 | =
847.8; | |
| approx.
| 20x20x10
2x0.002x1000 | = 1000. |
Where the calculations are too involved for the above
method to be used, the decimal point can be determined by the following rules,
which apply both to Model K and Model L.
A number having n figures to the left of the decimal point
shall be designated as having +n places. A decimal number
having n cyphers to the right of the decimal point, between
the decimal point and any number other than 0, shall be
designated as having –n places.
Thus the numbers —
|
5430000, | 674, |
81.2, |
7.82, |
0.45, |
0.0421, |
0.00675 |
| have | +7, | +3, |
+2, | +1, | +0, |
–1, | –2 |
places |
(See notes 1, 2 and 3
below.)
Multiplication
To find the number of places (p) in the product (P=XxY).
Let X have m places, and Y have n places. |
| RULE I. |
| p=m+n or
p=m+n–1. |
| (a) | When the result is
below the original setting
p=m+n. |
| Example: 3x4 (m=1;
n=1). |
| Set B to 3. Set 1 to T. Move T to 4. (This
is below setting.) p=m+n=2. Answer = 12. |
| (b) | When the result is
above the setting, the product has m+n–1
places. |
| Example: 3x3 (m=1; n=1) |
| Set B to 3. Set 1 to T. Move T to 3. (This is above
setting.) p=m+n–1 = 1. Answer = 9. |
| (See note 4 below.) |
Division
| To find the number of places
(q) in the quotient (Q = X/Y). |
| RULE. II. | |
q=m–n or
q=m–n+1
as follows: |
| (c) | When the result is
above the setting, the quotient has
m–n places. |
| Example: 3÷4 (m=1; n=1). |
| Set B to 3. Set 4 to T. Move T to 1. (This is above
setting.) q=m–n=0. Answer =
0.75. |
| (d) | When the result is below the
setting, the quotient has m–n+1 places. |
| Example: 5÷4 (m=1; n=1). |
| Set B to 5. Set 4 to T. Move T to 1. Read answer at
B. (This is below setting.) Therefore q = 1–1+1 = +1.
Answer = 1.25. |
| (See note 5 below.) |
Calculations involving Multiplication and Division
| RULE III. |
Two methods may be used in working out complex problems
involving both multiplication and division. They are: |
| (1) |
Taking numerator and denominator
alternately. |
| (2) |
Taking all the numerators first and
then dividing consecutively by the denominators. |
| Of these two methods, only the latter can be used if
the position of the decimal point is required. If the other is used,
the decimal point must be found by inspection. |
| First multiply consecutively the series of factors in
the numerator and then divide consecutively by the factors of the denominator.
|
| Take the algebraic sum of the places in the factors
of the denominator from the algebraic sum of the places in the
factors of the numerator, and to this result add the algebraic
sum of the results obtained from the application of Rules I
and II to the several steps of the problem. |
| Example:
|
|
432x32.4x0.0217x0.
98
0.00000621x412000x0.175x4.71
| = 141.14... |
| Number of places in factors of— |
| Numerator =
3+2+(–1)+0 | = +4 |
| Denominator =
–5+6+0+1 | = +2
|
| |
Difference | = +2 |
| Results of various steps in calculation =
-1 + 1 + 1 | = +1
|
| Number of places in
answer | = +3 |
| Answer =
141.14. | |
Notes on determining position of Decimal Point
| Note
|
| 1. | Thus: |
| 5430000.00 |
(7 figures are to
left of decimal point) |
has +7 places |
| 81.2 |
(2 figures to left of decimal point)
| has +2 places |
| 2. |
0.45 |
(no figures to left of decimal point,
and no noughts between decimal point and first figure other than 0, to right
of decimal point) |
has –0 places |
| 0.0421 |
(one nought between decimal point
and first figure to right of decimal point)
|
has –1 places |
| 3. | Left of
decimal
point | |
Right of
decimal point | No.
of
places |
| 5430000 | . | |
+7 |
| 674 | . |
| +3 |
| 81 | . |
2 | +2 |
| 7 | . |
82 | +1 |
| 0 | . |
45 | –0 |
| 0 | . |
0421 | –1 |
| 0 | . |
00675 | –2 |
| 4. |
MULTIPLICATION.
RULE I |
| When in the third movement of a multiplication
calculation the cursor is moved downwards the number of places
in the product (i.e. figures to the left of the decimal
point) is equal to the sum of the number of places in the
two terms of the calculation.
If the cursor is moved upwards the number of places in
the product is one less than the sum of the number of
places in the two terms of the calculation. |
| 5. | DIVISION.
RULE II |
| When in the third movement of a division calculation
the cursor is moved upwards the number of places in the
quotient is equal to the number of places in the dividend
minus the number of places in the divisor.
If the cursor is moved downwards the number of places
in the quotient is one more than the number of places in
the dividend minus the number of places in the divisor.
|
In summary form, the rules for finding the position of the
decimal point are:
When the cursor moves up, in multiplication, the result
has m+n–1 places.
When the cursor moves up, in division, the result has
m–n places.
When the cursor moves down, in multiplication, the result
has m+n places.
When the cursor moves down, in division, the result has
m–n+1 places.
The rules are expressed by the following diagram which it is
suggested the user should cut out and fix to the cursor of his
calculator with adhesive transparent tape.
 | X
÷ |
m+n–1
m–n |
|
 | X
÷ |
m+n
m–n+1 |
|
CARBIC LIMITED
54, Dundonald Road,
London, S.W.19
Printed in England
Notes:
- -
- Only approximately (logarithmic scales !),
but the nonlinear correction would be way less than the width of a mark scale,
so linear interpolation can be considered to be exact for all practical
purposes.
- -
- In the earlier (pre-decimalisation) version of
the manual, this sections reads: "The Sterling items must be reckoned as
decimals of pounds, shillings or pence as best suits the problem.", as in the
even earlier 8-page instructions.
(back)
- -
- This Otis King Manual has been HTML'ized by
Andries de Man
from a copy provided by
Dick
Lyon, courtesy of Ray Hems. Thanks to Dick Lyon for proofreading and
discussing this page.
Andries de Man 10/29/1997






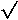 63
x 4000
63
x 4000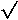 260000 x
421.82
260000 x
421.82
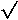 63 ?
63 ?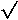 63 =
3.98.
63 =
3.98.