Raíces múltiples. Intersección con el eje de las abscisas.

[ Arriba ] [ Actividad 3.A ] [ Actividad 3.B ] [ Actividad 3.C ]

Recordemos que el orden de multiplicidad de una raíz es la cantidad de veces que esta raíz se repite como tal.
Para determinar el comportamiento de una función respecto del eje x (eje de las abscisas), hay que factorizar totalmente el polinomio y determinar el orden de multiplicidad de sus raíces.

Observemos lo ejemplos:

  1. P(x)=x2+2x+1=(x+1)(x+1)=(x+1)2

La raíz x=(-1) tiene multiplicidad 2 (par), y vemos que la gráfica toca el eje x pero no lo atraviesa, "rebota".

  1. Q(x)=x3-9x2+27x-27=(x-3)(x-3)(x-3)=(x-3)3

La raíz x=3 tiene multiplicidad 3 (impar) y vemos que la gráfica atraviesa el eje x, "lo corta"

  1. R(x)=(x+1)(x+1)(x+1)(x+1)(x-2)(x-2)(x-2)=(x+1)4(x-2)3

2, es raíz triple  => la gráfica atraviesa al eje x en x=2

-1 es raíz cuadruple => la gráfica toca al eje x en x=(-1)

En general, cuando una raíz r tiene:

Si deseamos conocer la multiplicidad de una raíz, debemos controlar que el polinomio este totalmente factorizado. Por ejemplo, erroneamente podriamos creer que x=(-6) es raíz doble de P(x)=(x+6)2(x2+x-30). Pero P(x) no está totalmente factorizado pues (x2+x-30)=(x+6)(x-5). Entonces, P(x)=(x+6)2(x+6)(x-5)=(x+6)3(x-5).
Ahora P(x) está totalmente factorizado y vemos que x=(-6) es raíz triple.

Ejercicios:

  1. Encontrar las raíces reales de los siguientes polinomios y determinar su multiplicidad.
    a) x4+x3-x2-x
    b) x3-5x2+7x-3
    c) 2x3-4x-8

  2. Según cada gráfico indicar si el orden de multiplicidad es par o impar.

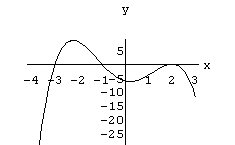    x=(-2)_ _ _ _ _
    x=1_ _ _ _ _    		 x=(-3)_ _ _ _ _ 
    x=(-1)_ _ _ _ _
    x=2_ _ _ _ _     		x=3_ _ _ _ _

  3. Siendo a, b, c, d, e y f números reales distintos, señalar que gráfico corresponde a cada uno de los siguientes polinomios y que relación de orden existe entre a, b y f:

    M(x)=(x-a)2(x-b)3


    N(x)=(x-c)(x-d)(x-e)


    T(x)=(x-f)4