MECANICA CELESTE Y SATELITAL

 

No se puede mencionar la mecánica celeste sin tener en cuenta las leyes de Kepler (Fig. 1) y  de Newton (Fig. 2).  

Fig. 1

Fig. 2

 

Cuando un cuerpo se mueve en el espacio, lo hace bajo la acción de una fuerza central y conservativa, que varía con el cuadrado de la distancia al centro en acción –“llámese Sol;  llámese  Tierra”. Esta no es la única teoría con la que se puede establecer aproximaciones a la ecuación con la que se obtiene la trayectoria de dicho cuerpo (planeta o satélite). Existen otras aproximaciones sostenidas por varios autores como Vogt (1996) y Tier (1992), es especialmente la de Vogt, -que si bien se limita a trayectorias elípticas o (cerradas)- permite una comprobación más fácil de las leyes de Kepler.

En todo movimiento de los planetas o satélites se comprueba que el momento angular (L) del cuerpo en cuestión es el vector producto del vector de posición (r), el vector velocidad  (v) y la fuerza (m), es decir (L = r x m  x  v )  donde:
.

L = momento angular

r  = vector de posición

m = masa

v  = velocidad

Como (L) se mantiene constante en dirección,  (r) y (v) estarán en un plano perpendicular a la dirección de  L (Fig. 3).

.  

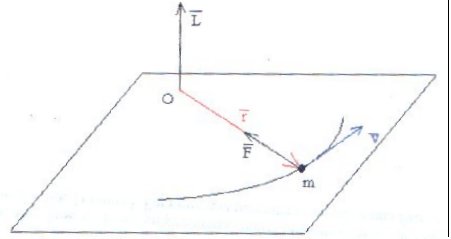
Fig. 3

El resultado de ésto es una trayectoria elíptica, vale decir una órbita cerrada.
Así que una elipse se define como el tipo de cónica  cuya excentricidad es menor que la unidad. Por lo tanto, un cuerpo sometido a una fuerza central atractiva e inversamente proporcional al cuadrado de la distancia al centro de la fuerza, describirá dicha trayectoria, por tener una energía total negativa
(E = < 1)
Cuando la órbita es abierta, como en una parábola, la energía total es 1, (E = 1).
Y cuando la órbita es también abierta como en una hipérbola, la energía total es  >1, (E = > 1).

El período está dado por el tiempo que tarda el móvil en dar una vuelta  completa en la órbita. 

Leyes de Kepler   1a Ley : “Los planetas describen órbitas elípticas estando el Sol en uno de sus focos” ( Fig. 4 )

Fig. 4

 

2^a Ley: “El vector posición de cualquier planeta respecto del Sol, barre áreas iguales de la elipse en tiempos iguales” (Fig. 5). 

3a Ley: “Los cuadrados de los  períodos son proporcionales a  los cubos de los semiejes mayores de la elipse” ( Fig. 6)

Fig. 5

  

¿Que son los elementos Keplerianos?

 

Fig. 6

Cuando un artefacto es colocado en órbita alrededor de la Tierra, describe trayectorias regidas  por las Leyes de Kepler y de la gravitación universal de Newton. Estas trayectorias son constantemente Tabuladas por organismos aerospaciales por Ej.: La NASA y permiten predecir los pasos de los mismos por el meridiano y latitud de un lugar.

Estos valores para cierta fecha y hora, pueden ser solicitados  vía Internet a: www.amsat.org

Donde, en el formato de 2 líneas de la NASA, o en formato AMSAT, pueden ser tomados  para ser cargados en los programas que permiten visualizar en una pantalla de PC su posición sobre un mapa, (el programa quik-track es muy utilizado por los radioaficionados para el seguimiento visua, como así el food-track que  permite el seguimiento con las antenas en los dos ejes de coordenadas).

 

La imagen a continuación  muestra el satélite Argentino de radioaficionados, LU-SAT ó  LO-19, con su lóbulo de irradiación.

(Pulsando sobre la imagen se producirá la animación del paso sobre Argentina en tiempo acelerado unas 90  veces  el real).

A continuación, Ej. de Keplerianos de 2 líneas del mismo satélite de radioaficionados  Argentino, LO19. Datos del 28/01/2000

Los números expresan cada uno de los elementos Keplerianos que componen ésta  tabulación, los que se enumeran a continuación.

 

T0 - Epoch: Número que especifica el momento que se fijaron los datos de un satélite
        determinado

 

M0 - Mean Anómali: Es el ángulo con valores constantes en el tiempo durante una
         revolución que va de 0º a 360º fijándose el 0º para el perigeo (punto orbital de la
         elíptica más cercano al Sol sobre el eje mayor de ésta) y 180º para el apogeo, (punto más
         alejado del Sol sobre el mismo eje) que marca la posición de un satélite en una órbita.

 

N0 - Mean Motion: Cantidad de órbitas en el día,o períodos orbitales.

 

I0 - Inclination: Es el Ángulo en grados formado entre el plano orbital y el plano
       ecuatorial de la tierra

 

E0 - Exentricity: Indica la forma de elipse orbital. Con E0 = 0, la elipse es un círculo; Con
        E0 = 1, la elipse es extremadamente elíptica.

 
W0 - Arg of Perigee: Es el ángulo en grados formado por la línea de  nodos y la línea de
         los ápsides  de la elipse.

O0 - RAAN (Rigt Ascention of Ascending Node): Es un ángulo medido en el centro de la
        Tierra  desde el equinoccio vernal hacia el nodo  ascendente.

K0 - Orbit Revolution:  Nº total de órbitas efectuadas.

Decay Rate: Éste valor indica el ritmo al cual, Mean Motion (N0) cambia debido a la
                     atracción u otros efectos relacionados (es un nº muy pequeño).  

Arriba:  “Esquema de Elementos Orbitales”

 

Visitando: http://celestrak.com/NORAD/elements/index.html, encontrará una muy extensa lista satelital con todos sus datos.

Dr. José C. Caldararo

Colaboró en la configuración y puesta en página el Sr. Eduardo De Tommaso.

 

GLOSARIO:

 

Ápside: Cada uno de los extremos del eje > de una órbita.

 

Línea de los ápsides: Es la línea que une dichos puntos.

 

Nodo: Cada uno de los dos puntos de intersección de la línea Nodal de un planeta  que atraviesa el plano de la Eclíptica.

 

Nodo ascendente: Es aquel donde la línea nodal pasa el plano de la eclíptica desde el hemisferio austral al boreal.

 

Nodo descendente: Es aquel donde la línea nodal pasa el plano de la eclíptica desde el hemisferio boreal al austral.

 

Solsticio: Cada uno de los puntos de tangencial de los trópicos con la eclíptica (para el hemisferio sur, es de verano el 22 de Diciembre y de Invierno el 21 de junio).

 

Equinoccio: Cada uno de los puntos de la esfera celeste en que la eclíptica corta el  ecuador celeste. Cuando el Sol pasa por éstos puntos, el día y la noche tienen igual duración.