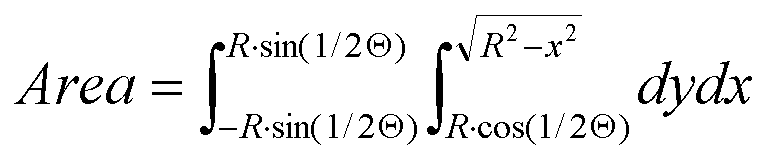
by
Erik Oosterwal
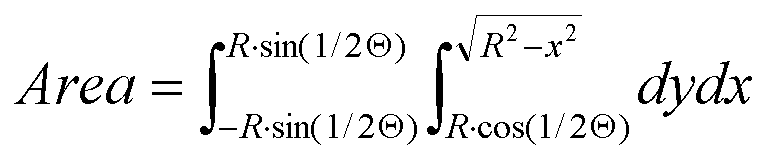
Of course we already know what area we want, we just need to know how long
of a cord to draw. With that in mind, if we know we need an area of
1/4 Pi·R we can use this formula:

That's still not real pretty but we end up with x being roughly 0.596027,
where x = h/R and h is the distance between the center of the cord and the
circle circumference. With a little more math we find that the length
of the cord needs to be 1.6059·R, with R being the radius of the
circle.
It really doesn't matter if you draw the cords parallel to the line that
goes through the center or not since the area outside the cord will be exactly
1/2 of the semi-circle (as long as the cord does not intersect the line drawn
through the circle's center.)
By now you may have guessed that there is a simpler solution that doesn't
require a degree in advanced mathematics, and you'd be right. As the
diagram below shows, you can draw 3 curved lines using a compass do divide
the circle into 4 equal sized parts:

That looks much simpler, doesn't it?
See all the brain teasers on The Puzzle Page.
Get daily puzzles in your RSS reader at The Puzzle Page Blog Site.
Looking for answers to computer programming problems?
Read what's going on in the Computer Science 101 classroom.