SITESWAP
Tudo que você sempre quis saber,
mas nunca teve coragem de perguntar.
(mesmo porque, você nunca soube o quê perguntar)
por Alexandre Roit
• O QUE É UM TRUQUE DE SITESWAP?
• OUTRAS INFORMAÇÕES CONTIDAS NAS SEQÜÊNCIAS DE LANÇAMENTO.
• QUAIS
AS DIFERENÇAS PRÁTICAS ENTRE
OS TRUQUES ESTÁTICOS E OS DINÂMICOS?
• COMO DETERMINAR AS TRANSIÇÕES?
O siteswap é um
sistema que foi inventado por volta de 1985 por três pessoas independentemente:
Paul Klimek da Universidade da Califórnia em Santa Cruz, Bruce "Boppo"
Tiemann na Caltech (Instituto de Tecnologia da Califórnia) e Michael
Day da Universidade de Cambridge. Jack Boyce – também da Caltech
– apareceu em seguida com os modelos de estado do malabares para explicar
o fenômeno dos truques dinâmicos (excited-state tricks).
Ele consiste numa seqüência de números que carrega uma série
de informações objetivas sobre os truques: número de
bolas envolvidas, ordem dos lançamentos e altura das bolas. Durante
muito tempo, o sistema teve algumas limitações, entre elas,
estar restrito a truques que tivessem lançamentos alternados –
uma mão de cada vez – eliminando assim os lançamentos
sincronizados, e não permitindo lançamentos ou pegadas de mais
de uma bola por vez – técnica batizada de multiplex,
na qual mais de uma bola é lançada por uma mão no mesmo
instante.
Atualmente estas limitações não existem, pois foram contempladas
por símbolos que permitem representá-las graficamente, não
só através do próprio siteswap, mas de outros
sistemas, como a ‘escada’, o ‘diagrama causal’ e a
‘MHN’ – Multi-handed Notation. Cada um destes sistemas é
usado para coisas específicas. O diagrama causal, por exemplo, é
ideal para truques de câmbio, onde dois malabaristas lançam objetos
um para o outro. De uma forma ou de outra, todos derivam do siteswap.
Com o avanço da tecnologia, fica cada vez mais fácil o acesso
a essas informações, bem como seu uso: a profusão de
páginas eletrônicas e programas de computador em torno do assunto
são intermináveis.
Sintaxe da palavra.
A tradução literal de siteswap é ‘troca
de lugares’. As variáveis desse sistema precisam ser compreendidas,
para que se entenda perfeitamente o sentido da explicação que
se segue, então sugiro que você leia este ponto depois de entendidos
os procedimentos da técnica, o que tentaremos esclarecer ao longo deste
texto.
Supondo que você só vai ler o próximo parágrafo
no final, aí vai a alegoria:
Tome por exemplo uma seqüência – digamos 55555 – e
escolha dois lançamentos: o segundo e o quinto, por exemplo. Agora
diga “Bolas, cheguem nas mãos uma no lugar da outra!”.
Como elas não vão fazer isso sozinhas, você tem que dar
uma ‘mãozinha’: a seqüência modificada –
com os ‘lugares trocados’ – é 58552. Continuamos
com nossa média de 5 – isso se nada caiu, porque um lançamento
com valor ‘8’ dentro de uma cascata com cinco bolas não
é nada fácil.
Sem pensar muito na resposta, serve
para: anotar e transmitir truques de malabares, descobrir novos truques, decupar
o aprendizado, de forma a entender as evoluções – os truques
– por partes, e compreender as relações existentes entre
um truque e outro. Com um bom uso destes dois últimos pontos, você
tem meios para lançar mão de truques que sirvam de educativo,
e conduzam a outros mais difíceis.
Não acredito, contudo, que o siteswap seja a ‘salvação
da lavoura’. Devemos ter cuidado de não nos esquecermos que ele
é apenas mais uma ferramenta de trabalho – para quem trabalha
com isso, obviamente – e não um fim em si. Aliás, pode
ser que nem seja do interesse de todos os malabaristas, ou que alguns não
se dêem bem com esta forma de aprendizado, mas tomar conhecimento dos
sistemas já desenvolvidos é quase uma obrigação.
O malabarista pode não usá-los por opção –
bem melhor do que não ter nenhuma opção.
Um músico pode se divertir matematicamente com suas combinações
harmônicas e melódicas, mas chega uma hora que só isso
não é suficiente, assim como para um poeta, saber de cor o dicionário
é de pouca utilidade.
Da mesma forma, um malabarista pode – e deve – se exercitar das
mais diversas maneiras, evoluindo suas capacidades e habilidades em todos
os sentidos.
A partir de um ponto, porém, ele tem a responsabilidade como artista
de dar forma a isso: achar seu público e, como em toda relação
cênica, propor seu jogo – jogo este, resultado da união
dos seus conhecimentos técnicos com as suas opções estéticas
– e se comunicar com sua platéia.
Uma coisa é certa: com mais e melhor técnica, os objetivos estéticos
são alcançados em menos tempo e com mais qualidade. Resultados
artísticos melhores estabelecem novas metas de evolução:
voltamos então ao desenvolvimento técnico. Essa bola de neve
só gera bons frutos, e eu pessoalmente espero que só siga na
direção de caminhos inexplorados do malabares, que com certeza
ainda tem muitos segredos a serem descobertos.
A idéia fundamental do siteswap
está em seguir uma ordem pré-determinada de lançamentos
dos objetos envolvidos num truque, ordem esta estabelecida por uma seqüência
de números. Estes números, que chamaremos valores de lançamento,
determinam a altura em que as bolas serão jogadas, em função
de uma unidade que chamaremos beat. Não importa como você
jogue malabares: a partir do momento que você lança e pega seus
objetos, existe um siteswap que descreve o que você faz.
Mas isso não é uma verdade absoluta. Se tomarmos por exemplo
a cascata convencional e o Mill’s Mess, teremos o mesmo siteswap
para ambos, que temos certeza serem dois truques bem diferentes.
Como o bom exemplo estabelece o caminho do bem, vamos pôr essas informações
em termos práticas. Vamos partir da cascata básica com três
bolas. Existem muitas coisas a serem analisadas, mas por ora vamos nos ater
aos seguintes pontos:
• As mãos fazem lançamentos alternados.
• Todo lançamento vai de uma mão para a outra –
já que estamos falando da cascata básica com três bolas.
• Entre um lançamento de uma bola e seu lançamento seguinte,
outros dois lançamentos são realizados.
OBS: doravante, o espaço de tempo entre um lançamento e o lançamento seguinte será chamado de beat.

O eixo horizontal representa o
tempo, e o eixo vertical, o espaço entre as mãos. Portanto,
este é o diagrama do espaço-tempo da cascata com três
bolas.
Vamos destacar a trajetória de uma das bolas para entendermos melhor:

Algumas conclusões:
• Se considerarmos N como sendo o número de
beats entre o lançamento de uma bola e seu lançamento
seguinte, esta mesma bola leva N-1 beats para chegar
na mão do seu próximo lançamento.
• Ao traçar uma linha vertical (a linha tracejada) em qualquer
ponto do diagrama, veremos que ela é cruzada por três linhas:
esta é a quantidade de bolas que temos no nosso truque.
• Em nenhum momento mais de uma linha chega ou sai da mesma mão.
• Todas as bolas levam três beats entre um lançamento
e outro.
Vamos avançar um pouco mais.
Vamos fazer um truque simples e ver como se comporta o diagrama. Faremos uma evolução com duas bolas na mesma mão e voltaremos à cascata.
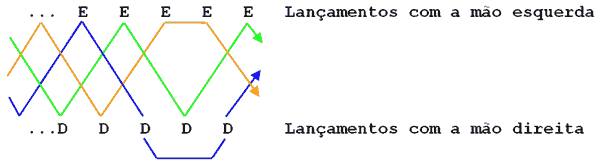
Temos duas novas informações
no nosso diagrama: a mão direita faz um lançamento para ela
mesma, enquanto a mão esquerda segura uma bola por mais tempo que o
normal. Não que alguém precise de um diagrama para entender
que isso acontece quando jogamos duas bolas na mesma mão, mas este
entendimento vai nos ajudar mais para frente.
As informações que temos com clareza no diagrama:
• A bola que sai da mão direita para ela mesma leva quatro beats
para ser lançada novamente.
• A bola que fica na mão esquerda leva dois beats para
ser lançada novamente.
Vamos agora estudar o diagrama do chuveirinho com três bolas:
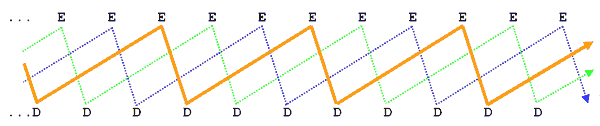
Se acompanharmos a bola destacada, veremos que sua trajetória alterna um longo tempo da mão direita para a mão esquerda – cinco beats, para ser exato – e apenas um beat da mão esquerda para a direita.
Estes diagramas nos mostram quantos
lançamentos acontecem entre um lançamento feito com uma bola
e o seguinte feito com a mesma bola.
Ele se propõe a acompanhar a bola de sua origem ao seu destino e quanto
tempo ela leva para isso, respeitando a unidade de tempo-espaço que
chamamos de beat. É exatamente isso que faz o siteswap,
só que através de representações numéricas:
determina o tempo entre lançamentos, a origem e o destino dos objetos
jogados.
A forma como isso é feito – se pelas costas, por baixo da perna
ou com rebotes – bem como o tempo que estas bolas permanecem na mão,
ficam a cargo do malabarista que estiver executando o truque. Ainda bem, pois
se não acreditássemos nisso, o Mill’s Mess nunca teria
sido inventado.
A representação numérica
dos truques acima fica assim:
• 333 ou simplesmente 3 – Cascata.
— Cada mão alternadamente lança os objetos a uma altura
que permite que dois outros lançamentos sejam feitos antes do lançamento
seguinte deste primeiro objeto.
• 42 – Duas bolas numa mão e uma parada na outra.
— Enquanto uma mão joga duas bolas, a outra mão fica para
com uma bola. Para que a mão que está parada alterne os movimentos
com a outra, a seqüência é 4440.
• 51 – Chuveirinho.
— Uma mão joga todas as bolas a uma altura que permite que as
outras duas bolas passem por dois lançamentos cada antes do seu lançamento
seguinte, ou seja, quatro outros lançamentos são feitos antes
do próximo feito com esta bola. Se analisarmos a perspectiva da outra
mão, veremos que os objetos são passados em um beat
desta para a outra e imediatamente lançados.
As explicações acima
são bem mais complicadas que a ação, mas a questão
aqui não é o truque, e sim como relacionar as seqüências
numéricas com a ação necessária para realizar
o truque proposto.
Vale sempre reforçar que a alternância das mãos é
mais importante que a ordem das bolas, no que concerne a seqüência
numérica.
Isso será assunto recorrente.
No ponto seguinte está a explicação de como entender
o significado dos números – os valores de lançamento –
de seus valores e de suas posições dentro de uma seqüência.
O QUE É UM TRUQUE DE SITESWAP?
Como já vimos, um truque é descrito por uma seqüência de números. Cada número se refere à altura e posição que a bola deve ser jogada. A velocidade das mãos permanece a mesma, não importando as variações que você faça, desde que estas sejam variações ‘legais’ de siteswap. A relação entre as alturas dos lançamentos dentro de um mesmo beat é determinada pela seguinte fórmula:
Hn=Hm*((n-1)/(m-1))2
Onde n e m são números de bolas, e Hn e Hm as alturas necessárias para os lançamentos. Se partirmos do valor de lançamento ‘3’ – a cascata normal com três bolas – teremos aproximadamente a seguinte progressão nas alturas:
| VALOR DE LANÇAMENTO | ALTURAS RELATIVAS AO MESMO BEAT ( METROS) | |
3 |
0.20 |
1.00 |
4 |
0.52 |
2.64 |
5 |
1.00 |
5.06 |
6 |
1.62 |
8.27 |
7 |
2.40 |
12.25 |
As mãos trabalham sempre
alternadamente, como na cascata normal. Os números ímpares da
seqüência são lançamentos feitos para a mão
oposta, enquanto os números pares são lançamentos feitos
para mesma mão que os fez.
‘0’s e ‘2’s merecem atenção especial.
Se respeitarmos a fórmula acima, a altura dos ‘2’s será
insignificante – e para a mesma mão que lança –
portanto substituímos este lançamento por uma espera de um beat.
Um ‘1’ é uma passada direta de mão a mão.
Note que necessariamente o próximo valor de lançamento será
relativo à bola que acabou de ser passada, sem nenhum outro evento
antes. Um ‘0’ significa que a mão ficará vazia durante
aquele beat.
Já existem várias formas de siteswap para que se coloque
no papel os truques, mas vamos nos restringir às seqüências
feitas com alternância de mãos – os ‘box’
estão descartados – e apenas um objeto é lançado
ou pego por cada mão – o que elimina os ‘multiplex’.
Apesar destas restrições, existe um número interminável
de seqüências ‘legais’ de siteswap. Mas o
que é uma seqüência legal?
A prática mais uma vez determina o conhecimento.
Tomemos uma seqüência qualquer, um 531.
Este truque, sendo jogado sem interrupção, será representado
assim:
| LANÇAMENTO | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| VALOR | 5 | 3 | 1 | 5 | 3 | 1 | 5 | 3 | 1 | 5 | 3 | 1 |
| MÃO | D | E | D | E | D | E | D | E | D | E | D | E |
>>>>>>>>>>>>>>>>>>>
L I N H A DO T E M P O >>>>>>>>>>>>>>>>>>>>>>>>>> |
||||||||||||
As cores representam cada bola
e as suas posições à medida que o tempo passa.
No caso do 531, todas as bolas são lançadas de uma mão
e pegas pela outra – já que todos os valores são ímpares.
Adiante:
Lembra da regra?
SE CONSIDERARMOS N COMO SENDO O NÚMERO DE BEATS ENTRE O LANÇAMENTO DE UMA BOLA E SEU LANÇAMENTO SEGUINTE, ESTA MESMA BOLA LEVA N-1 BEATS PARA CHEGAR NA MÃO DO SEU PRÓXIMO LANÇAMENTO.
Se a regra for seguida, faremos com que as bolas sigam suas trocas de posições sem se encontrarem na mesma posição em nenhum momento. Apenas uma bola é lançada por vez, garantindo a legalidade da seqüência.
Com outro olhar sobre a tabela
acima conseguiremos localizar duas diferentes órbitas, se considerarmos
as trocas de posição das bolas até voltarem à
posição inicial: (5,1) e (3).
Ou seja, duas bolas se revezam no (5,1) enquanto uma fica no (3). Vamos fazer
o mesmo com a seqüência 504:
| LANÇAMENTO | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| VALOR | 5 | 0 | 4 | 5 | 0 | 4 | 5 | 0 | 4 | 5 | 0 | 4 |
| MÃO | D | E | D | E | D | E | D | E | D | E | D | E |
>>>>>>>>>>>>>>>>>>>
L I N H A DO T E M P O >>>>>>>>>>>>>>>>>>>>>>>>>> |
||||||||||||
Neste caso, a órbitas é
(5,4): Todas as bolas fazem a mesma trajetória.
Perceba que as posições ocupadas pelo valor de lançamento
‘0’ não têm cor, ou seja, a mão está
vazia. Lembra da regra?
UM ‘0’ SIGNIFICA QUE A MÃO FICARÁ VAZIA DURANTE AQUELE BEAT.
Ainda seguindo com as verificações,
nos certificamos que não existem conflitos.
Para que não precisemos fazer uma linha enorme de números para
chegar a esta conclusão, basta que contemos as posições
dentro da própria seqüência até projetarmos todos
os lançamentos. No caso do 531 fica assim:
• 5 3 1 – Para avançar
as cinco posições do primeiro lançamento, avance as duas
primeiras até o valor ‘1’ e retome a contagem a partir
do próprio ‘5’. Você cairá novamente no ‘1’.
• 5 3 1 – Posição ocupada. Em seguida, avance as
três posições do segundo lançamento, que vai chegar
no próprio ‘3’.
• 5 3 1 – Posição ocupada. Por fim, avançando
uma posição referente ao último lançamento, ocuparemos
a última posição vazia, o ‘5’.
• 5 3 1 – Todas as posições ocupadas.
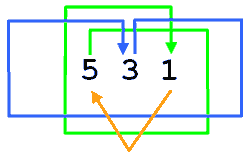
Tente com o 504.
OUTRAS
INFORMAÇÕES CONTIDAS NAS
SEQÜÊNCIAS DE LANÇAMENTO.
Se você subtrair de cada um dos números da sua seqüência, o número real de objetos que você tem, você terá uma seqüência cuja soma é zero. Por exemplo, o 7562 é um truque com cinco objetos.
O NÚMERO REAL DE OBJETOS É DESCOBERTO PELA SEGUINTE FÓRMULA: 7+5+6+2=20/4=5, ONDE QUATRO É A QUANTIDADE DE VALORES DE LANÇAMENTO CONTIDA NA SUA SEQÜÊNCIA.
Continuando. Subtraímos 5 de cada posição, e teremos;
-7
5 6 2
-5-5-5-5
-- 2+0+1-3=0
O primeiro passo foi cumprido. Vamos ver que outras informações podem-se obter a partir dos números acima.
Partiremos do principio que cada
um dos números a que chegamos ocupa uma posição ‘x’,
e que seus valores numéricos determinam para quais posições
eles irão, como fizemos na verificação de conflitos com
o 531 e 504.
• Se você avançar duas posições a partir
do ‘2’, você cai no ‘1’.
• Avance uma posição a partir do ‘1’ e você
cai no ‘-3’.
• Se você avançar menos três posições
– ou três posições para trás – a partir
do ‘-3’ você cai no ‘2’.
• Permaneça com o ‘0’ na mesma posição.
As trocas de posições foram realizadas sem que nenhuma nova posição tivesse conflito. Isto mantém a validade da nossa seqüência. Atenção: apesar do procedimento ser o mesmo, quando fizemos isso com o 531 e 504, estávamos trabalhando com a seqüência de lançamentos propriamente dita. A verificação que acabamos de executar se refere aos menores valores de referência para uma seqüência válida. Pode parecer que trocamos seis por meia dúzia, mas adiante isso voltará à pauta.
Conflitos também podem ser verificados pela seguinte fórmula:
![]()
Onde ‘j’ é o valor do lançamento da posição ‘i’, e ‘m’ é o valor do lançamento da posição ‘k’: havendo igualdade, teremos duas bolas caindo ao mesmo tempo e na mesma mão.
Vamos analisar uma outra seqüência.
Considere o 771, outro truque com
cinco objetos (7+7+1=15/3=5). Depois de feitas as devidas subtrações
e trocadas as posições, perceberemos que se trata de mais uma
seqüência válida. Verificando:
• Teremos um ‘2’, outro ‘2’ e um ‘-4’.
Nossa soma é zero.
• A partir do primeiro ‘2’, avançamos para a posição
do ‘-4’.
• Se contarmos as quatro posições negativas a partir do
‘-4’, teremos que ‘sair’ da seqüência até
chegarmos na posição do segundo ‘2’.
• Ao avançarmos as duas posições a partir do segundo
‘2’, teremos novamente que ‘sair’ da seqüência
até chegarmos no primeiro ‘2’.
Nenhum conflito de posições, já que não houve
encontros. Entretanto, duas das trocas só foram possíveis porque
as posições foram alcançadas após uma ‘saída’
da seqüência.
Na seqüência anterior
(o 7562), as trocas aconteceram sem que precisássemos ‘dar a
volta’ para chegar a posição final. Nenhuma troca saiu
do âmbito do próprio truque.
Chegamos a uma nova informação: a existência de duas qualidades
de truques, os truques estáticos (ground state tricks) e os
truques dinâmicos (excited state tricks), onde os estáticos
são seqüências que se comportam como a 7562 e os dinâmicos
como a seqüência 771.
A verificação dessa qualidade de truques só pode ser
feita a partir do menor valor de referência de uma seqüência,
já que se tentarmos fazer isso diretamente com os números da
seqüência, chegaremos a truques dinâmicos apenas.
Existem outras propriedades matemáticas nas seqüências,
mas por ora, são estas que nos interessam.
QUAIS
AS DIFERENÇAS PRÁTICAS ENTRE OS
TRUQUES ESTÁTICOS E OS DINÂMICOS?
Uma diferença entre eles
é que os truques estáticos podem ser iniciados a partir da cascata
convencional, e o mesmo não acontece com os truques dinâmicos;
nestes casos, são necessárias as ‘transições’,
que serão tratadas adiante. Esta regra também é válida
para o inverso – sair dos truques de volta para a cascata. Uma conseqüência
disto é a possibilidade de se estabelecer uma “seqüência
de seqüências de truques estáticos” sem nenhum problema
para passar de um a outro, exceto lembrar qual seqüência você
escolheu.
Com os truques dinâmicos isto é impossível. Uma vez começados,
os truques dinâmicos podem, assim como os estáticos, ser repetidos
quantas vezes você quiser, entretanto eles requerem uma ordem específica
de lançamentos antes de serem iniciados. Uma nova ordem específica
de lançamentos será também necessária para que
se retorne à cascata convencional. Em extensão a isso, não
podemos combinar os truques dinâmicos de qualquer jeito: para cada caso
serão necessárias combinações diferentes, as ditas
‘transições’, tanto para iniciar como para encerrar
um truque dinâmico ou uma seqüência deles (isto não
impede que o final da seqüência de um truque dinâmico seja
correspondente à transição para o truque dinâmico
seguinte, mas isto é tecnicamente chamado de ‘acaso’).
COMO DETERMINAR AS TRANSIÇÕES?
Vamos partir do malhado chuveirinho,
que tem sua representação numérica dada por um 51. Feitas
as contas, concluiremos que se trata de um truque dinâmico. Vamos estabelecer
então um procedimento para ‘inventar’ transições
que nos permitam passar da cascata normal para o chuveirinho sem que haja
conflito.
Escreveremos a seguinte seqüência, imaginando que os lançamentos
“x” devam ser preenchidos pelos valores da nossa transição...
. . . 3 3 3 3 3 3 x x 5
1 5 1 5 1 5 1 . . .
. . . . . . . . . . . . . . . . . . . . . .
Os pontos embaixo da seqüência serão substituídos por um ‘*’ cada vez que determinarmos a nova posição de um lançamento...
? ? 3 3 3 3 3 3 x x 5 1
5 1 5 1 5 1 . . . .
? ? ? ? ? * * * * * * . * . * * * * * * . *
Os pontos sem ‘*’ são justamente os “endereços dos nossos ‘x’”. Vamos então escolher as possibilidades menos óbvias, mandando o primeiro ‘x’ para o segundo ponto, o que nos obriga a substituir a letra pelo número 5. O segundo ‘x’ será substituído por um 2, determinando a seguinte seqüência:
? ? ? 3 3 3 3 3 3 5 2
5 1 5 1 5 1 5 1 . . . .
? ? ? ? ? ? * * * * * * * * * * * * * * * . *
Isso significa que da cascata para o chuveirinho, lançamos a primeira bola, esperamos um beat e seguimos com o truque. Se você quiser aumentar este tempo de pausa – para fazer uma pirueta, por exemplo – você pode aumentar a quantidade de ‘x’ para 4 e chegar a seguinte seqüência:
. . . 3 3 3 3 3 3 7 2 2 2 5 1 5 1 5 1 5 1 . . .
Outra possibilidade ainda, é substituir o primeiro ‘x’ por um 3, o que preenche o primeiro ponto, e trocar o segundo ‘x’ por um 4, mandando ele para o segundo ponto. Fica assim:
. . . 3 3 3 3 3 3 3 4 5 1 5 1 5 1 5 1 . . .
Isso nos dá uma transição
interessante, mas pouco usada.
O mesmo procedimento usado para estabelecermos uma transição
de entrada num truque dinâmico deve ser usado para estabelecer a saída.
Tente você mesmo fazer a saída do chuveirinho retornando à
cascata.
31 Chuveirinho
com duas bolas.
441 Um truque muito feito com claves, onde o ‘1’
é feito por trás das costas.
53 O meio chuveirinho (half-shower) com quatro bolas.
531 Um truque muito simpatico com três bolas.
5313 A versão assimétrica do truque acima.
55500 O “flash” com três bolas.
50505 O “chase” com três bolas: todas lançadas
de uma mão antes de serem lançadas pela outra.
5551 Parecido com o “chase”, mas feito com quatro
bolas, e uma mão sempre achando que é um chuveirinho.
55514 Um truque bem bacana com quatro bolas: três fazem
o “flash”, enquanto outra corre por fora, transitando de 1 para
4 e de 4 para 1.
453 Um truque de quatro muito legal. Tente fazer com o ‘4’
por fora.
55550 O primeiro educativo com quatro bolas para jogar cinco.
Use as seqüências abaixo para se exercitar, tirando todas as informações possíveis: quantidade de objetos, validade dos truques, órbitas existentes, tipo de truque (dinâmico ou estático) e, óbvio, se você consegue jogá-lo.
633
633633633633633633633633633633633633633633633633633
61616
616166161661616616166161661616616166161661616616166
642
642642642642642642642642642642642642642642642642642
6424
6424642464246424642464246424642464246424642464246424
66661
66661666616666166661666616666166661666616666166661
56414
56414564145641456414564145641456414564145641456414
645
645645645645645645645645645645645645645645645645645
661515
661515661515661515661515661515661515661515661515
71
7171717171717171717171717171717171717171717171717171
771
771771771771771771771771771771771771771771771771771
777171
777171777171777171777171777171777171777171777171777171
723
723723723723723723723723723723723723723723723723723723
7272712
72727127272712727271272727127272712727271272727127272712
75751
7575175751757517575175751757517575175751757517575175751
7562
75627562756275627562756275627562756275627562756275627562
7161616
71616167161616716161671616167161616716161671616167161616
70701
7070170701707017070170701707017070170701707017070170701
7531
75317531753175317531753175317531753175317531753175317531
741
741741741741741741741741741741741741741741741741741741741
714
714714714714714714714714714714714714714714714714714714714
7571
75717571757175717571757175717571757175717571757175717571
67561
6756167561675616756167561675616756167561675616756167561
17170170
17170170171701701717017017170170171701701717017017170170
801
801801801801801801801801801801801801801801801801801801801
Siteswap FAQ
De Allen Knutson, atualizado pela última vez em 10/NOV/1993.
(Juggling Information Service – www.juggling.org)
Siteswaps: Early Posts
by Bengt, et al
Mensagens organizadas por Peter Mark.
(Juggling Information Service – www.juggling.org)
The Mathematics of Juggling
– parte de The Science of Juggling
De Peter J. Beek e Arthur Lewbel.
(Juggling Information Service – www.juggling.org)
SiteSwaps – How To
Write Down A Juggling Pattern:
A Guide
For The Perplexed
Copyright (C) Solipsys Ltd, 1996
(Juggling Information Service – www.juggling.org)