MC1

Método de Monte Carlo

Corresponde a um método que utiliza a técnica de amostragem, por números aleatórios (método estocástico), para chegar à solução aproximada de certos problemas matemáticos sem a determinação da solução analítica do sistema (Pacitti & Atkinson, 1983; Bruns et al.,1981). O método de Monte Carlo foi desenvolvido em 1949 por Metrópolis e Ulam (Metrópolis & Ulam, 1949, apud Bruns et al.,1983), mas já era de conhecimento de vários cientistas que iniciaram a moderna computação digital, tais como Metrópolis, Ulam, Von Newmann, Kahn, Fermi, entre outros (Kalos & Whitlock, 1986), que investigaram este método estocástico quando trabalhavam no desenvolvimento de armamento nuclear no laboratório científico de Los Alamos para o departamento de Defesa dos Estados Unidos, durante a segunda guerra mundial. O nome Monte Carlo se deve ao fato de ser um método estocástico, fazendo lembrar os jogos de azar do mundialmente famoso cassino de Monte Carlo. Como a essência do método é probabilistica, vamos analisar o mecanismo para gerar números aleatórios, que é a parte principal do Método de Monte Carlo.

Números Aleatórios

Números aleatórios, na verdade, não são números gerados por um processo aleatório, tal como uma moeda atirada para o ar. Ao contrário, são números gerados por um processo aritmético inteiramente determinado e o grupo de números resultantes em conseqüência terá várias propriedades estatísticas que, quando reunidas, são denominadas aleatórias (Scheid, 1975). Desta forma, os números aleatórios são melhor denominados de números pseudo-aleatórios.

Para se obter números pseudo-aleatórios é necessário um gerador destes números. Esses números aleatórios tem sido gerados por uma série de processos físicos, usualmente envolvendo um gerador de ruído eletrônico para produzir uma seqüência de pulsos (Lowry, 1970). Existem rotinas para gerar números aleatórios escritas nas mais variadas linguagens de programação (BASIC, LISP, PASCAL, FORTRAN, C, C⁺⁺, etc) que, a partir de um número inicial (semente), usa-se um processo de recorrência para obter uma seqüência de números pseudo-aleatórios. Como exemplo, podemos obter números aleatórios por meio do seguinte algorítmo:

R_n+1=(13*R_n*mod(100))/100

Onde mod(100), nesse caso, tem a seguinte definição: dado R_n, então R_n+1 é o resto da divisão de 13*R_n por 100, o resultado é novamente dividido por 100, gerando números entre 0 e 1, igualmente espaçados, utilizando a aritmética inteira ou de ponto fixo (Pacitti & Atkinson, 1983). Caso R₀=1, a seqüência gerada é esta:

0.1300, 0.6900, 0.9700, 0.6100, 0.9300, 0.0900, 0.1700, 0.2100, 0.7300, 0.4900, 0.3700, 0.8100, 0.5300, 0.8900, 0.5700, 0.4100, 0.3300, 0.2900, 0.7700, 0.0100, 0.1300, 0.6900, 0.9700, 0.6100, 0.9300, 0.0900, 0.1700, 0.2100, 0.7300, 0.4900, 0.3700, 0.8100, 0.5300, ...

Depois de surgir o número 0.01, a seqüência começa a se repetir. Para rotinas geradoras de números aleatórios, vide apêndice

Uma questão muito discutida diz respeito a aleatoriedade dos números gerados. Nem sempre o que é aleatório numa aplicação computacional, será aleatório em outra aplicação (Press et al, 1995). Há uma série de testes estatísticos para verificar esta aleatoriedade. Para testarmos se uma seqüência de números aleatórios gerados está distribuída uniformemente no intervalo de 0 a 1, calculamos os momentos, cujo resultado esperado está mostrado a seguir:

1^o Momento:

para N->¥

2^o Momento:

para N->¥

3^o Momento:

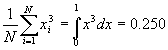para N->¥

Integração Numérica usando Método de Monte Carlo

Imagine que queiramos calcular a área sob a curva mostrada:

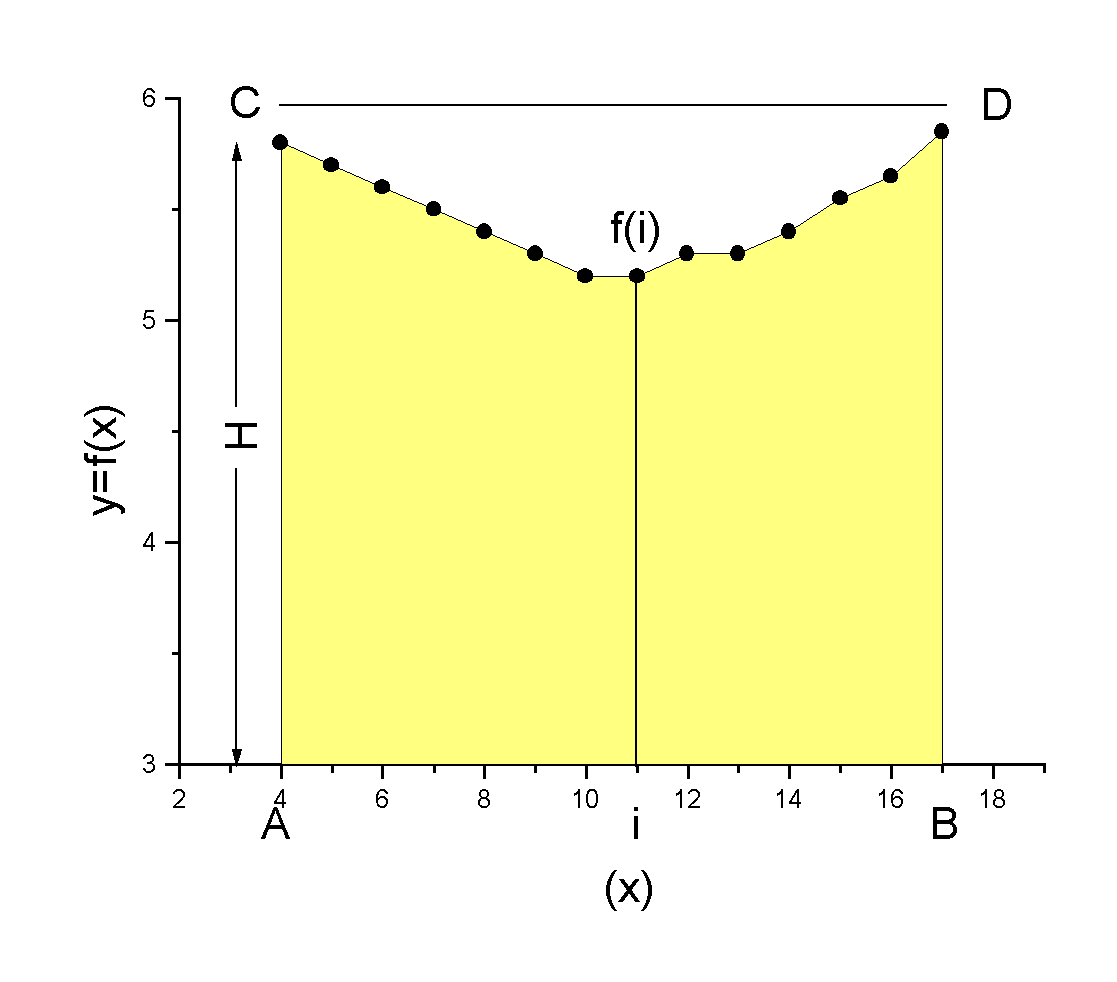
Fig-1: Esboço de uma técnica de integração numérica, apenas como exemplo

O retângulo ABCD mostrado na Fig-1, construído no intervalo [A,B], com altura H, tem área igual a H.(B-A). Gerando-se um par de números aleatórios entre 0 e 1 (N1,N2), podemos obter um novo par de números aleatórios (xrand, yrand) a partir dos anteriores que caem dentro da área do retângulo ABCD, como segue:

xrand = (B-A)*N1+A

yrand = H*N2

Os pontos (xrand, yrand) podem cair dentro ou fora da área abaixo da curva (área hachurada), i.e, podem estar acima ou abaixo dos pontos (i, f(i) ). Se gerarmos N pares aleatórios dentro do retângulo ABCD, e sendo N_d a quantidade de pares ordenados aleatórios que caem na região abaixo da curva e N_fa quantidade que cai fora da curva, teremos:

N_d + N_f = N

f_d + f_f= 1

sendo

f_d a fração de pontos aleatórios gerados abaixo da curva e f_f a fração de pontos gerados fora da curva mas dentro do retângulo ABCD, onde:

f_d = N_d/N e f_f = N_f/N

Como a área abaixo da curva é dada por:

e a área de todo o retângulo ABCD é dada por:

H*(B-A)

Para N -> ¥ , os pontos gerados aleatoriamente preenchem toda a área do retângulo ABCD, logo, podemos aproximar:

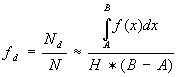
logo, a área sob a curva pode ser obtida por:

Uma outra forma de calcular a integral, bem menos custosa do ponto de vista computacional, é a que parte da definição de integral, como segue:

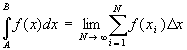
onde

Para N -> ¥ , podemos aproximar a integral para:

Com este tipo de aproximação, o custo computacional é menor pois ao invés de gerarmos um par de número aleatória por interação, geramos apenas um número aleatório (x_i) para cada passo. Estes dois métodos de integração numérica mostrados anteriormente correspondem ao Método de Monte Carlo.

Vamos agora, calcular o valor de algumas integrais usando o método de Monte Carlo. O programa a seguir descreve o procedimento anterior para calcular uma integral qualquer no intervalo de A a B, e está escrito no Matlab Software Corporation

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%PROGRAMA DE CÁLCULO DE INTEGRAIS DEFINIDAS PRÓPRIAS VIA

%MÉTODO DE MONTE CARLO

%Entre com os valores do limite inferior (li) e superior (ls) da

%integral

li;

ls;

pi=3.1415926;

s=0;

%CALCULE A FUNÇÃO PARA UM TOTAL DE N PASSOS, IMPRIMINDO

%O VALOR DA INTEGRAL A CADA 1000 EVOLUÇÕES

for i=1:1000

for j=1:1000

x=(li+(ls-li)*rand);

% s=s+(escreva a funcao f(x))

s=s+x;

end

N=i*1000;

monte(i,1)=((ls-li)*s)/N;

end

plot(monte)

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Cálculo da Integral

cuja evolução por Monte Carlo está mostrada no gráfico a seguir:

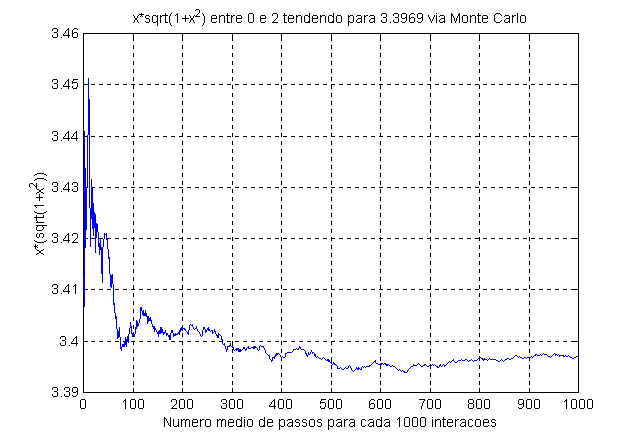
Fig-2: Evolução por Monte Carlo da integral tendendo para 3,3969 após 10⁶ passos

Há vários métodos de integração numérica, sendo bastante conhecidos na literatura os métodos retangular, trapezoidal e parabólico (Regra de Simpson). Vamos comparar o valor da integral acima entre estes três métodos e o método de monte carlo.

Método de Integração numérica	Valor de convergência
Método Retangular	3.3934
Método Trapezoidal	3.3934
Método Parabólico	3.3934
Método de Monte Carlo	3.3969

Podemos notar na tabela anterior que o método de Monte Carlo fornece um valor para integral que diferencia dos demais métodos nas duas últimas casas decimais, mostrando-se menos eficiente. Mas para integrais mais complexas ou para um número de passos maior o Método de Monte Carlo torna-se mais eficiente.

Vejamos outro exemplo. Vamos calcular o valor da integral

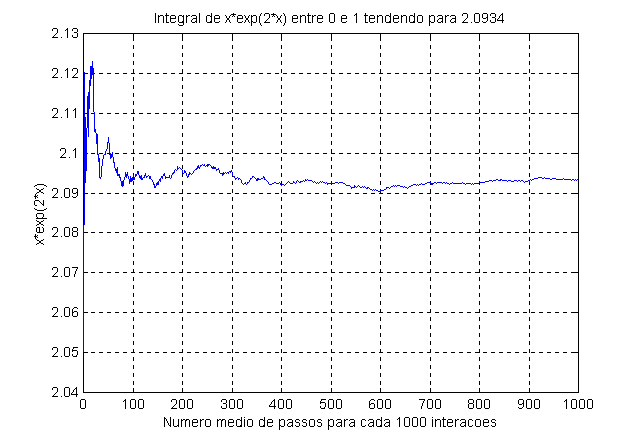
Fig-3: O valor esperado é 2,0973 e o valor obtido por Monte Carlo após 10⁶ passos corresponde a 2,0934

Agora vamos usar o método de Monte Carlo para simulações de problemas físicos.

Na simulação, o método de Monte Carlo consiste em gerar valores aleatórios e, a partir deles, gerar uma função de distribuição a fim de obter os valores médios da grandeza procurada. Vamos simular o crescimento de um polímero de 20 monômeros com efeito de volume excluido. Geramos aleatoriamente a posição do primeiro monômero e a partir dele, geramos um par de números aleatórios entre 0 e 1 e impomos a seguinte condição:

Se o primeiro número aleatório estiver entre 0 e 1/3 e o segundo não, cresce o polímero (coloca-se o próximo monômero) na direção de x positivo, caso contrário cresce o polímero na direção de x negativo

Se o primeiro número aleatório estiver entre 1/3 e 2/3 e o segundo não, cresce o polímero (coloca-se o próximo monômero) na direção de y positivo, caso contrário cresce o polímero na direção de y negativo

Se o primeiro número aleatório estiver entre 2/3 e 1 e o segundo não, cresce o polímero (coloca-se o próximo monômero) na direção de z positivo, caso contrário cresce o polímero na direção de z negativo

Construimos uma rede vazia na qual inserimos o polímero e em seguida completamos com soluto, também aleatoriamente, para podermos observar o efeito de volume excluido. Se o ponto da rede que formos crescer o polímero estiver ocupado com soluto, tentamos crescer o polímero em outra direção (novamente de maneira aleatória). Uma vez construído o polímero, medimos as distância de ponta a ponta (end-to end distace) e contruimos a função de distribuição do vetor end-to-end.

Este programa de construção do polímero com efeito de volume excluído foi feito em liguagem C.

/***********************************************/

#include <stdio.h>

#include <time.h>

#include <math.h>

/*****construindo a rede******/

int latt[55][55][55];

int f, xsol[300000], ysol[300000], zsol[300000], a, b, xsol2, ysol2,

zsol2, c;

int i, j, k, ii, jj, kk, ww, wx[21], wy[21], wz[21], ran, c, nsol,

f, contador, k, kont,w;

float rann, r, q, rnd;

int x[21], y[21], z[21], passo, t;

int testar(xsol2,ysol2,zsol2)

int xsol2,ysol2,zsol2;

{

int i,j,s;

s=1;

for (i=0; i<nsol; i++) {

if (xsol[i]==xsol2 && ysol[i]==ysol2 && zsol[i]==zsol2)

{

s = 0;

}

return s;

}

void distr_soluto()

{

int flag, nsol, contt, n;

/**quantidade de soluto na rede**/

n=100;

for (b=0; b<=nsol*8; b++) {

n++;

/*printf(" %d \n", n); */

/*while(flag==0) {*/

/** GERANDO SOLUTO ALEATORIAMENTE **/

rann =(double) (lrand48()/2147483647.0);

xsol2 =(int)(4+(46*(lrand48()/2147483647.0)));

ysol2 =(int)(4+(46*(lrand48()/2147483647.0)));

zsol2 =(int)((4+(46*(lrand48()/2147483647.0))));

/*printf( "%d %d %d %d \n " , flag, xsol2, ysol2, zsol2);*/

flag = testar(xsol2, ysol2,zsol2);

if (flag==1) {

xsol[b]=xsol2;

ysol[b]=ysol2;

zsol[b]=zsol2;

/*printf( "%d %d %d %d \n " , flag, xsol2, ysol2, zsol2); */

nsol =100;

}

for (a=1; a<2; a++) { /** COLOCANDO UM UNICO SOLUTO DE FORMA CUBICA **/

contt=0;

xsol[a]=xsol[b];

ysol[a]=ysol[b];

zsol[a]=zsol[b];

contt++;

latt[xsol[a]][ysol[a]][zsol[a]]=2.0;

/*printf("%d [%d][%d][%d] \n", contt, xsol[a], ysol[a], zsol[a]);*/

xsol[a]=xsol[a]+1;

ysol[a]=ysol[a];

zsol[a]=zsol[a];

latt[xsol[a]][ysol[a]][zsol[a]]=2.0;

contt++;

/*printf("%d [%d][%d][%d] \n", contt, xsol[a], ysol[a], zsol[a]);*/

xsol[a]=xsol[a]-1;

ysol[a]=ysol[a]+1;

zsol[a]=zsol[a];

contt++;

latt[xsol[a]][ysol[a]][zsol[a]]=2.0;

/*printf("%d [%d][%d][%d] \n", contt, xsol[a], ysol[a], zsol[a]);*/

xsol[a]=xsol[a];

ysol[a]=ysol[a]-1;

zsol[a]=zsol[a]+1;

latt[xsol[a]][ysol[a]][zsol[a]]=2.0;

contt++;

/*printf("%d [%d][%d][%d] \n", contt, xsol[a], ysol[a], zsol[a]);*/

xsol[a]=xsol[a]+1;

ysol[a]=ysol[a]+1;

zsol[a]=zsol[a]-1;

latt[xsol[a]][ysol[a]][zsol[a]]=2.0;

contt++;

/*printf("%d [%d][%d][%d] \n", contt, xsol[a], ysol[a], zsol[a]);*/

xsol[a]=xsol[a]-1;

ysol[a]=ysol[a];

zsol[a]=zsol[a]+1;

latt[xsol[a]][ysol[a]][zsol[a]]=2.0;

contt++;

/*printf("%d [%d][%d][%d] \n", contt, xsol[a], ysol[a], zsol[a]);*/

xsol[a]=xsol[a]+1;

ysol[a]=ysol[a]-1;

zsol[a]=zsol[a];

latt[xsol[a]][ysol[a]][zsol[a]]=2.0;

contt++;

/*printf("%d [%d][%d][%d] \n", contt, xsol[a], ysol[a], zsol[a]);*/

xsol[a]=xsol[a];

ysol[a]=ysol[a]+1;

zsol[a]=zsol[a];

latt[xsol[a]][ysol[a]][zsol[a]]=2.0;

contt++;

/*printf("%d [%d][%d][%d] \n", contt, xsol[a], ysol[a], zsol[a]);*/

}

int testar_rede(x2,y2,z2)

int x2,y2,z2;

{

int i,j,s;

s=1;

if (latt[x2][y2][z2]!= 0)

{

s = 0;

}

return s;

}

int distr_polimero()

{

int nmon=0, c, contt, k, colocou;

c=0;

k=0;

while((nmon<1) && (k<30)){

k++;

ran =(int)(15+(15*(lrand48()/2147483647.0)));

/* printf(" ran=%i ", ran);*/

if ( ran < 25) {

wx[nmon] = ran-1;

wy[nmon] =ran ;

wz[nmon] =ran+1;

}

else {

wx[nmon] = ran;

wy[nmon] =ran +1;

wz[nmon] =ran+2;

}

/* printf(" nmon = %d \n", nmon);*/

if (testar_rede(wx[nmon],wy[nmon],wz[nmon])==1){

latt[wx[nmon]][wy[nmon]][wz[nmon]]=1;

/* printf(" %d \n", nmon);*/

/* printf( " %d %d %d \n " ,wx[nmon],wy[nmon],wz[nmon]); */

nmon++;

}

if ( k>=30) {

ran =(int)(15+(15*(lrand48()/2147483647.0)));

wx[nmon] = ran-1;

wy[nmon] =ran ;

wz[nmon] =ran+1;

/* printf( " %d \n " ,latt[wx[nmon]][wy[nmon]][wz[nmon]]) ;*/

if (testar_rede(wx[nmon],wy[nmon],wz[nmon])==1){

latt[wx[nmon]][wy[nmon]][wz[nmon]]=1;

/* printf(" %d \n", nmon);*/

printf( " %d %d %d \n " ,wx[nmon],wy[nmon],wz[nmon]);

nmon++;

}

while(nmon<20) {

/*for (nmon=1; nmon<=20; nmon++) {*/

rann =(double) (lrand48()/2147483647.0);

rnd =(double) (lrand48()/2147483647.0);

if (rnd>=0.5) {

passo=1;

}

else{

passo=-1;

}

colocou = 0;

a=0;

while((colocou == 0) && (a <2))

{

/*printf( "condicao x %d %d %d=nmon \n", colocou, a, nmon); */

if ((rann<=0.33) || (colocou==0)) {

wx[nmon]=wx[nmon-1]+passo;

wy[nmon]=wy[nmon-1];

wz[nmon]=wz[nmon-1];

if(testar_rede(wx[nmon],wy[nmon],wz[nmon])==1){

latt[wx[nmon]][wy[nmon]][wz[nmon]] = 1.0;

/*printf(" nmon = %d \n", nmon);*/

/*printf( " %d %d %d \n " ,wx[nmon],wy[nmon],wz[nmon]); */

nmon++;

colocou=1;

}

else

a++;

}

a=0;

while((colocou ==0) && (a<2))

{

/*printf( "condicao y %d %d %d=nmon \n", colocou, a, nmon);*/

if ((rann > 0.33 && rann < 0.66 ) || (colocou == 0)) {

wy[nmon]=wy[nmon-1]+passo;

wx[nmon]=wx[nmon-1];

wz[nmon]=wz[nmon-1];

if(testar_rede(wx[nmon],wy[nmon],wz[nmon])==1){

latt[wx[nmon]][wy[nmon]][wz[nmon]] = 1.0;

/*printf("nmon = %d \n", nmon);*/

/*printf( " %d %d %d \n " ,wx[nmon],wy[nmon],wz[nmon]); */

nmon++;

colocou =1;

}

else

a++;

}

a=0;

while((colocou ==0) && (a<2))

{

/*printf( "condicao z %d %d %d=nmon \n", colocou, a, nmon);*/

if ((rann>=0.66) || (colocou ==0)) {

wz[nmon]=wz[nmon-1]+passo;

wy[nmon]=wy[nmon-1];

wx[nmon]=wx[nmon-1];

if(testar_rede(wx[nmon],wy[nmon],wz[nmon])==1){

latt[wx[nmon]][wy[nmon]][wz[nmon]] = 1.0;

/*printf(" nmon =%d \n", nmon);*/

/*printf( " %d %d %d \n " ,wx[nmon],wy[nmon],wz[nmon]); */

nmon++;

colocou=1;

}

else{

a++;

}

if (colocou == 0)

{ return 0;

}

else

{ return 1;

/**********************************************/

for (ii=0; ii<=55; ii++) {

for (jj=0; jj<=55; jj++) {

for (kk=0; kk<=55; kk++) {

latt[ii][jj][kk]=0;

latt[ii][jj][0]=2;

latt[ii][0][kk]=2;

latt[0][jj][kk]=2;

latt[ii][jj][55]=2;

latt[55][jj][kk]=2;

latt[ii][55][kk]=2;

}

distr_soluto();

distr_polimero();

}

/*}*/

/*printf(" %d \n", k);*/

}

main()

{

int i, j, c, d, k, ran1, cont, h, contt, resp;

int xsol2, ysol2, zsol2, flag =0;

contador=0;

for (ii=0; ii<=55; ii++) {

for (jj=0; jj<=55; jj++) {

for (kk=0; kk<=55; kk++) {

latt[ii][jj][kk]=0;

latt[ii][jj][0]=2;

latt[ii][0][kk]=2;

latt[0][jj][kk]=2;

latt[ii][jj][55]=2;

latt[55][jj][kk]=2;

latt[ii][55][kk]=2;

}

for (i=0; i<100000; i++) { /* numero de passos da simulacao */

cont=0;

contt=0;

nsol =0;

for (ii=0; ii<=55; ii++) {

for (jj=0; jj<=55; jj++) {

for (kk=0; kk<=55; kk++) {

latt[ii][jj][kk]=0;

latt[ii][jj][0]=2;

latt[ii][0][kk]=2;

latt[0][jj][kk]=2;

latt[ii][jj][55]=2;

latt[55][jj][kk]=2;

latt[ii][55][kk]=2;

}

do {

for (ii=0; ii<=55; ii++) {

for (jj=0; jj<=55; jj++) {

for (kk=0; kk<=55; kk++) {

latt[ii][jj][kk]=0;

latt[ii][jj][0]=2;

latt[ii][0][kk]=2;

latt[0][jj][kk]=2;

latt[ii][jj][55]=2;

latt[55][jj][kk]=2;

latt[ii][55][kk]=2;

}

distr_soluto();

resp = distr_polimero();

}while(resp ==0);

contador++;

/*****calcular distacia end to end **************************/

r=(double)(sqrt(pow((wx[19]-wx[0]),2.0)+pow((wy[19]-wy[0]),2.0)+pow((wz[19]-wz[0]),2.0)));

printf(" %i %f \n ", contador, r);

/* printf("%f \n ", r); */

}

printf(" \n FIM DO PROGRAMA!!! \n");

}

/**********************************************************/

O resultado do programa:

A função de distribuição da distância end-to-end está mostrada no gráfico seguinte:

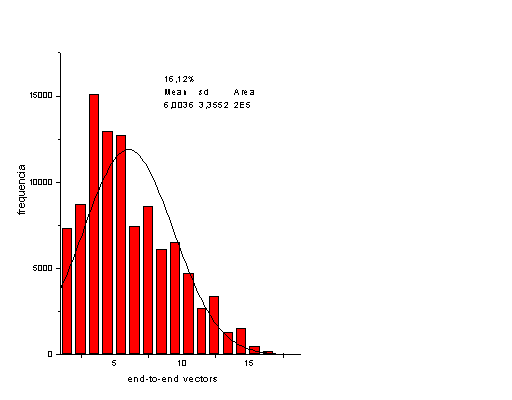
Fig-02: Histograma da distância end-to-end para 100000 passos de MC, na construção de um polímero com 20 monômeros e efeito de volume excluído. O valor médio da distância end-to-end é de 6.00± 3. O desvio padrão foi alto devido o número de passos ser relativamente pequeno para podermos realizar uma boa estatística

Apesar da estatística ser "pobre", o valor média da distância end-to-end está de acordo com a Teoria de Flory para estatísticas de polímero, no qual Flory mostrou que para uma cadeia com volume excluído, a distância end-to-end média <R> varia com o comprimento da cadeia da seguinte forma:

Para o polímero simulado, temos:

Apêndice

Aqui encontramos algumas rotinas para gerar números aleatórios bastante usadas pela comunidade científica. Estas rotinas foram extraídas do Numerical Recipes in Fortran - The Art of Scientific Computing (vide referência)

Primeira rotina - RAN0

***********************************************************************************
FUNCTION RAN0(IDUM)

DIMENSION V(97)

DATA IFF /0/

IF(IDUM.LT.0.OR.IFF.EQ.0)THEN

IFF=1

ISEED=ABS(IDUM)

IDUM=1

DO 11 J=1,97

DUM=RAN(ISEED)

11 CONTINUE

DO 12 J=1,97

V(J)=RAN(ISEED)

12 CONTINUE

Y=RAN(ISEED)

ENDIF

J=1+INT(97.*Y)

IF(J.GT.97.OR.J.LT.1)PAUSE

Y=V(J)

RAN0=Y

V(J)=RAN(ISEED)

RETURN

END

**********************************************************************************

Segunda Rotina - RAN1

**********************************************************************************

FUNCTION RAN1(IDUM)

DIMENSION R(97)

PARAMETER (M1=259200,IA1=7141,IC1=54773,RM1=3.8580247E-6)

PARAMETER (M2=134456,IA2=8121,IC2=28411,RM2=7.4373773E-6)

PARAMETER (M3=243000,IA3=4561,IC3=51349)

DATA IFF /0/

IF (IDUM.LT.0.OR.IFF.EQ.0) THEN

IFF=1

IX1=MOD(IC1-IDUM,M1)

IX1=MOD(IA1*IX1+IC1,M1)

IX2=MOD(IX1,M2)

IX1=MOD(IA1*IX1+IC1,M1)

IX3=MOD(IX1,M3)

DO 11 J=1,97

IX1=MOD(IA1*IX1+IC1,M1)

IX2=MOD(IA2*IX2+IC2,M2)

R(J)=(FLOAT(IX1)+FLOAT(IX2)*RM2)*RM1

11 CONTINUE

IDUM=1

ENDIF

IX1=MOD(IA1*IX1+IC1,M1)

IX2=MOD(IA2*IX2+IC2,M2)

IX3=MOD(IA3*IX3+IC3,M3)

J=1+(97*IX3)/M3

IF(J.GT.97.OR.J.LT.1)PAUSE

RAN1=R(J)

R(J)=(FLOAT(IX1)+FLOAT(IX2)*RM2)*RM1

RETURN

END

*********************************************************************************

Terceira rotina - RAN2

**********************************************************************************

FUNCTION RAN2(IDUM)

PARAMETER (M=714025,IA=1366,IC=150889,RM=1.4005112E-6)

DIMENSION IR(97)

DATA IFF /0/

IF(IDUM.LT.0.OR.IFF.EQ.0)THEN

IFF=1

IDUM=MOD(IC-IDUM,M)

DO 11 J=1,97

IDUM=MOD(IA*IDUM+IC,M)

IR(J)=IDUM

11 CONTINUE

IDUM=MOD(IA*IDUM+IC,M)

IY=IDUM

ENDIF

J=1+(97*IY)/M

IF(J.GT.97.OR.J.LT.1)PAUSE

IY=IR(J)

RAN2=IY*RM

IDUM=MOD(IA*IDUM+IC,M)

IR(J)=IDUM

RETURN

END

**********************************************************************************

Quarta Rotina - RAN3

***********************************************************************************

FUNCTION RAN3(IDUM)

C IMPLICIT REAL*4(M)

C PARAMETER (MBIG=4000000.,MSEED=1618033.,MZ=0.,FAC=2.5E-7)

PARAMETER (MBIG=1000000000,MSEED=161803398,MZ=0,FAC=1.E-9)

DIMENSION MA(55)

DATA IFF /0/

IF(IDUM.LT.0.OR.IFF.EQ.0)THEN

IFF=1

MJ=MSEED-IABS(IDUM)

MJ=MOD(MJ,MBIG)

MA(55)=MJ

MK=1

DO 11 I=1,54

II=MOD(21*I,55)

MA(II)=MK

MK=MJ-MK

IF(MK.LT.MZ)MK=MK+MBIG

MJ=MA(II)

11 CONTINUE

DO 13 K=1,4

DO 12 I=1,55

MA(I)=MA(I)-MA(1+MOD(I+30,55))

IF(MA(I).LT.MZ)MA(I)=MA(I)+MBIG

12 CONTINUE

13 CONTINUE

INEXT=0

INEXTP=31

IDUM=1

ENDIF

INEXT=INEXT+1

IF(INEXT.EQ.56)INEXT=1

INEXTP=INEXTP+1

IF(INEXTP.EQ.56)INEXTP=1

MJ=MA(INEXT)-MA(INEXTP)

IF(MJ.LT.MZ)MJ=MJ+MBIG

MA(INEXT)=MJ

RAN3=MJ*FAC

RETURN

END

**********************************************************************************

Quinta Rotina - RAN4

***********************************************************************************

FUNCTION RAN4(IDUM)

PARAMETER (IM=11979,IA=430,IC=2531,NACC=24)

DIMENSION INP(64),JOT(64),KEY(64),POW(65)

DATA IFF/0/

IF(IDUM.LT.0.OR.IFF.EQ.0)THEN

IFF=1

IDUM=MOD(IDUM,IM)

POW(1)=0.5

DO 11 J=1,64

IDUM=MOD(IDUM*IA+IC,IM)

KEY(J)=(2*IDUM)/IM

INP(J)=MOD((4*IDUM)/IM,2)

POW(J+1)=0.5*POW(J)

11 CONTINUE

NEWKEY=1

ENDIF

ISAV=INP(64)

IF(ISAV.NE.0)THEN

INP(4)=1-INP(4)

INP(3)=1-INP(3)

INP(1)=1-INP(1)

ENDIF

DO 12 J=64,2,-1

INP(J)=INP(J-1)

12 CONTINUE

INP(1)=ISAV

CALL DES(INP,KEY,NEWKEY,0,JOT)

RAN4=0.0

DO 13 J=1,NACC

IF(JOT(J).NE.0)RAN4=RAN4+POW(J)

13 CONTINUE

RETURN

END

***********************************************************************************

Referências Bibliográficas

Bruns, W; Motoc, I; O’Driscoll, K.F; "Monte Carlo Applications in Polymer Science"; (27), Lecture Notes in Chemistry; (1981); Springer-Verlag

Kalos, M.H; Whitlock, P.A; "Monte Carlo Methods", (1986), Vol.01, John Wiley & Sons, Inc.

Lowry, G,G; "Markov Chains and Monte Carlo Calculations in Polymer Science", (1970), Marcel Dekker, Inc

Metropolis, N; Ulan, S.M; "The Monte Carlo Method", J.Am.Statist.Assoc., (44), (1949), 335

Pacitti, T; Atkinson, C.P; "Programação e Métodos Computacionais", (1983), Vol-02, LTC Editora

Press, W.H; Teukolsky, S.A; Vetterling, W.T; Flannery, B.P; "Numerical Recipes in C - The Art of Scientific Computing", (1995), Cambridge University Press

Press, W.H; Teukolsky, S.A; Vetterling, W.T; Flannery, B.P; "Numerical Recipes in Fortran - The Art of Scientific Computing", (1990), Cambridge University Press

Scheid, F; "Introdução à Ciência dos Computadores", (1975), Editora McGraw-Hill do Brasil