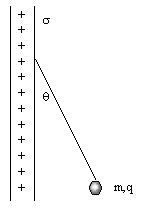| FLUXO DO CAMPO ELÉTRICO |
Vamos iniciar
por uma idéia simples e intuitiva. Quem ouve rádio no verão em
Porto Alegre está a todo momento sendo informado que passam tantos
carros por minuto no posto da Polícia Federal da auto-estrada. Quanto
maior o número de carros por minuto, maior o fluxo. Pronto, já
introduzimos o conceito de fluxo. Da mesma forma, o proprietário de
uma loja mede a sua clientela pela quantidade de gente que passa pela
porta de entrada, em determinado intervalo de tempo.
Qualquer que seja o caso, veremos facilmente que o
fluxo depende da quantidade daquilo que flui e da área através da
qual passa o "fluido". Portanto, quanto maior o número de
clientes ou quanto maior a porta de entrada, maior será o fluxo de
clientes para o interior da loja.
Essa noção intuitiva está na origem daquilo que
podemos denominar fluxo do campo elétrico (E). Numa primeira
abordagem, podemos dizer que
Fluxo de campo elétrico = intensidade de campo elétrico X área
perpendicular ao campo
Logo veremos que essa definição é
muito simplificada, e tem pouco valor operacional, porque em geral o
valor de E varia ao longo da superfície, e nem sempre esta é
perpendicular ao campo. Podemos melhorar a definição, dividindo a
superfície em elementos tão pequenos quanto possível, de modo que E
seja constante nessa área infinitesimal. A esta área associamos um
vetor  ,
cuja direção é perpendicular à área e cujo módulo é igual à área.
Podemos manter a idéia intuitiva definindo fluxo infinitesimal, ,
cuja direção é perpendicular à área e cujo módulo é igual à área.
Podemos manter a idéia intuitiva definindo fluxo infinitesimal,
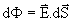 (3.1)
(3.1)
Assim, o fluxo através de determinada área S é dado
pela integral de superfície
 (3.2)
(3.2)
No caso de uma superfície fechada, o vetor área é
convencionalmente dirigido de dentro para fora. O fluxo através de
uma superfície fechada é assim representado
 (3.3)
(3.3)
|
A LEI DE GAUSS
A arte no uso da lei de Gauss reside na boa escolha da superfície
Gaussiana.
Não esqueça, siga a simetria da distribuição de cargas!
Demonstre o que está sendo dito ao lado, sobre a aproximação de
plano infinito.
Demonstre como um cilindro finito pode ser considerado infinito.
|
Seja uma carga Q. Imagine uma superfície qualquer,
fechada, envolvendo esta carga. A lei de Gauss estabelece que
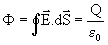 (3.4)
(3.4)
A lei de Gauss é válida para qualquer
situação, com campo uniforme, ou não, e para qualquer tipo de
superfície fechada, também denominada superfície Gaussiana.
Todavia, para ser operacionalmente útil ela deve ser usada apenas em
determinadas circunstâncias. Uma circunstância favorável ocorre
quando a superfície Gaussiana é tal que o produto escalar entre o
campo e o vetor superfície é facilmente obtido.
Isso é sempre possível quando a distribuição de
cargas apresenta alta simetria. Existem três tipos de simetrias que
facilitam o uso da lei de Gauss
- Simetria planar;
- Simetria cilíndrica ou axial;
- Simetria esférica.
A simetria planar aplica-se no caso de uma distribuição de cargas
num plano infinito, ou no caso em que se possa fazer a aproximação
de plano infinito. Por exemplo, um plano finito pode ser considerado
infinito, se o campo elétrico for calculado num ponto muito próximo
do plano. Isto é, se a distância do plano ao ponto for muito menor
do que as dimensões do plano.
A simetria cilíndrica, ou axial, aplica-se no caso de uma distribuição
linear infinita. Existem dois casos clássicos:
- Linha infinita de cargas;
- Cargas distribuídas num cilindro infinito.
De modo análogo ao caso anterior, um cilindro finito pode ser
considerado infinito em determinadas circunstâncias.
Existem dois casos típicos de simetria esférica:
- Carga puntiforme;
- Distribuição esférica de cargas.
Veremos mais adiante como usar a lei de Gauss para calcular o campo
devido a cada uma dessas distribuições.
|
LEI DE GAUSS
&
LEI DE COULOMB
|
A lei de Gauss e a lei de Coulomb são formas
diferentes de abordar o mesmo problema. Portanto, o cálculo do campo
elétrico para determinada distribuição de carga fornece o mesmo
resultado, quer seja realizado através de uma ou outra lei.
Então, quando e por que usar uma ou outra lei?
Como regra, o uso de uma ou outra lei é determinado pelas seguintes
circunstâncias:
- Distribuição de cargas com alta simetria
 Lei de Gauss
Lei de Gauss
- Distribuição de cargas com baixa simetria
 Lei de Coulomb
Lei de Coulomb
|
CAMPO DE UMA CARGA PUNTIFORME

|
Por argumentos de simetria, é fácil chegar à
conclusão de que o campo de uma carga puntiforme deve ter simetria
esférica. Isto é, o valor do campo é o mesmo para qualquer ponto
sobre uma esfera. Mais do que isso, o campo deve ser normal a esta
esfera.
Portanto, a melhor Gaussiana para calcular o campo
a uma distância r de uma carga puntiforme é uma esfera de raio r.
Em qualquer ponto sobre a Gaussiana, o produto
escalar será simplesmente EdS. Então, tendo em conta que E é
constante, teremos
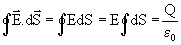
A integral fechada sobre a superfície
corresponde à área da esfera, 4pr2.
Portanto, o campo de uma carga puntiforme, q, a uma distância r, é
dado por
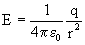 (3.5)
(3.5)
Como era de se esperar, a expressão (3.5) é
igual à expressão (2.3), obtida com o uso da lei de Coulomb.
|
DISTRIBUIÇÃO ESFERICAMENTE SIMÉTRICA
Um condutor em equilíbrio eletrostático sempre apresentará campo
nulo em seu interior
Grosso modo, num material não-condutor a carga fica onde a colocamos
|
No caso de uma distribuição de cargas com
simetria esférica, convém distinguir algumas situações. Em
primeiro lugar, dependendo do material o tratamento será bem
diferente.
- Material condutor - Já sabemos que quando uma certa
quantidade de carga elétrica é colocada num material condutor,
ela se distribuirá de modo a manter o campo nulo no interior do
material. Numa esfera a carga ficará uniformemente distribuída
na sua superfície. Portanto, para um material condutor não há
diferença entre uma esfera e uma casca esférica. Em ambos os
casos, a carga elétrica se distribuirá uniformemente na superfície
externa.
- Material dielétrico - Quando o material é não-condutor,
a situação é bem diferente. A carga não se distribui como no
caso do condutor; grosso modo, ela fica onde a colocamos. Para
esse tipo de material não é suficiente conhecermos a quantidade
de carga, há que se saber a forma como ela está sendo distribuída.
Isto é, necessitamos conhecer a densidade de carga no interior do
material. Portanto, em termos de cálculo de campo elétrico e uso
da lei de Gauss, uma esfera dielétrica pode ser bastante
diferente de uma casca esférica.
|
ESFERA CONDUTORA
|
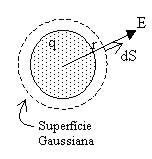
Já vimos acima que no caso de material condutor,
pouco importa se temos uma esfera maciça, oca ou se temos uma simples
casca esférica; qualquer que seja o objeto, o campo interno sempre
será nulo.
De modo análogo ao caso da carga puntiforme,
argumentos de simetria nos levam à conclusão de que o campo de uma
esfera condutora tem simetria esférica, de modo que a melhor
Gaussiana será uma esfera concêntrica com a distribuição de
cargas. O campo é igual ao de uma carga puntiforme, dado na eq.
(3.5).
Portanto, uma esfera condutora de raio R
comporta-se, para pontos externos, r>R, como se toda sua carga
estivesse concentrada no seu centro.
|
ESFERA DIELÉTRICA


|
Vamos considerar o caso em que a distribuição de
cargas é uniforme. Isto é, a densidade r,
dada em C/m3, é constante. Poderíamos ter uma distribuição
mais complexa, na qual a densidade variasse com a distância ao
centro.
- Região I - r > Raio da distribuição (R)
O cálculo é análogo ao do campo de uma
carga puntiforme. O resultado tem a mesma forma apresentada na eq.
(3.5). Se a carga total, Q, for conhecida, basta colocá-la no lugar
de q. Se ao invés disso, conhecermos a densidade, r,
então a carga será dada pelo produto da densidade pelo volume da
esfera, Q=4pR3r/3,
resultando
 (3.6)
(3.6)
A carga que aparece na lei de Gauss
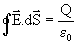
é aquela envolvida pela superfície Gaussiana, isto é, a carga no
interior do volume 4pr3/3. Se
conhecemos a densidade de carga, teremos Q=4prr3/3.
O campo no interior da esfera será dado por
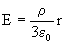 (3.7)
(3.7)
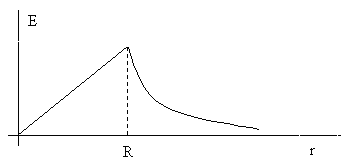
O variação do campo, em função do raio, é
representada na figura abaixo.
|
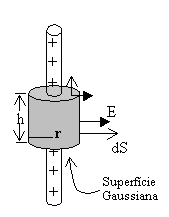
DISTRIBUIÇÃO LINEAR INFINITA
|
A distribuição linear infinita ocorre quando as
cargas são distribuídas numa linha infinita, ou num cilindro
infinito. Em ambos os casos tem-se geralmente uma densidade linear
uniforme, l.
Argumentos de simetria permitem concluir que o
campo apresenta simetria cilíndrica. Isto é, a intensidade é a
mesma em qualquer ponto da superfície lateral de um cilindro, cujo
eixo coincide com o eixo da distribuição da cargas, e a direção é
perpendicular a esta superfície lateral.
É óbvio que a superfície Gaussiana mais
apropriada é o cilindro indicado na figura ao lado. A integral
fechada da lei de Gauss pode ser desdobrada, transformando-se numa
soma de integrais de superfície, ao longo das bases do cilindro e ao
longo da superfície lateral.
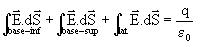
Em qualquer ponto das bases, os vetores E
e dS são perpendiculares entre si, de modo que as duas primeiras
integrais são nulas. Na superfície lateral, o campo é constante e
tem a mesma direção do vetor dS. Portanto,
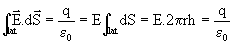
A carga no interior da Gaussiana é q=lh.
Portanto, o campo criado por uma distribuição linear infinita, a uma
distância r do eixo da distribuição, é dado por

|
PLANO INFINITO DE CARGAS
|
Vamos considerar uma distribuição infinita de
cargas, com densidade uniforme +s, conforme
figura abaixo.
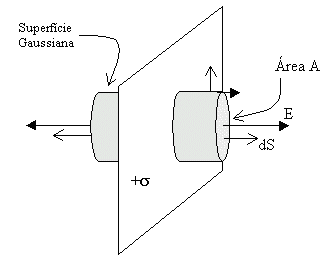
Por simetria conclui-se que o campo é
perpendicular ao plano de cargas, e que sua intensidade é constante
ao longo de qualquer plano paralelo ao plano de cargas. Portanto, o
cilindro da figura acima é uma boa escolha como superfície
Gaussiana. De modo análogo ao procedimento adotado no caso da
simetria cilíndrica, a integral fechada pode ser desdobrada em
integrais abertas, ao longo das bases e da superfície lateral da
Gaussiana.

Em qualquer ponto da superfície lateral, os
vetores E e dS são mutuamente perpendiculares, de modo que o produto
escalar é nulo. Por outro lado, tanto na base1, quanto na base2, E é
constante e paralelo a dS, de modo que

A carga no interior da superfície
Gaussiana é q=sA, resultando
 (3.9)
(3.9)
|
EXERCÍCIOS

Figura 3.1
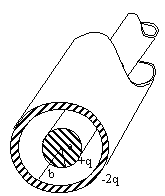
Figura 3.2

Figura 3.3
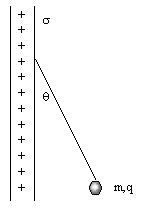
Figura 3.4
|
3.1 Uma rede de caçar borboleta está
numa região onde existe um campo elétrico uniforme, como ilustra a
figura 3.1. A extremidade aberta é limitada por um aro de área A,
perpendicular ao campo. Calcule o fluxo de E através da rede.
3.2 Uma linha infinita de cargas produz
um campo de 3x104 N/C a uma distância de 3 m. Calcule a
densidade linear de carga.
R.: 5x10-6 C/m
3.3 A figura 3.2 mostra parte de dois
longos e finos cilindros concêntricos de raios a e b. Os cilindros
possuem cargas iguais e opostas, com densidade linear l.
Use a lei de Gauss para mostrar que: (a) E=0 para r<a e (b) entre
os cilindros

3.4 A figura 3.3 mostra um cilindro
condutor muito longo, de comprimento L, contendo uma carga +q e
envolvido por uma fina casca cilíndrica, também condutora e de
comprimento L, contendo uma carga –2q. Use a lei de Gauss para
calcular: (a) o campo elétrico na região externa à casca cilíndrica;
(b) A distribuição de cargas na parte interna e na parte externa da
casca cilíndrica; (c) o campo elétrico na região entre os
cilindros.
R:(a)E=(1/2pe0)(q/Lr), apontando
de fora para o centro do cilindro; (b)-q em cada superfície; (c)idem
ao ítem (a), apontando do centro do cilindro para fora.
3.5 Um cilindro infinitamente longo, de
raio R, contém uma carga uniformemente distribuída, com densidade r.
Mostre que a uma distância r do eixo do cilindro (r<R),

3.6 A figura 3.4 mostra uma esfera
com massa m e carga q, suspensa no campo gravitacional da terra por um
fio de seda que faz um ângulo q com uma
placa não condutora infinita e uniformemente carregada. Calcule a
densidade superficial de carga da placa, s.
R: s=2mge0tgq/q
3.7 A figura 3.5 mostra duas placas
infinitas com suas superfícies internas carregadas com densidades
superficiais de carga +s e -s.
Determine o campo elétrico: (a) na região à esquerda das placas;
(b) na região entre as placas; (c) na região à direita das placas.
R: E=0 fora do capacitor; E=s/e0
no interior do capacitor.
3.8 Uma fina casca esférica metálica
de raio ra possui uma carga qa. Concêntrica com esta casca, existe
outra fina casca metálica de raio rb (rb>ra)
e carga qb. Calcule o campo elétrico nas regiões onde:
(a) r<ra; (b) ra<r<rb; (c)
r>rb.
R: (a)E=0; (b)E=(1/4pe0r)(qa);
(c)E=(1/4pe0r)(qa+qb)
3.9 A figura 3.6 mostra uma esfera
condutora de raio ra, com carga +q, concêntrica com uma
casca esférica condutora de raios rb e rc e
carga -2q. Calcule o campo elétrico nas regiões em que: (a) r<ra;
(b) ra<r<rb; (c) rb<r<rc;
(d) r>rc. (e) Use a lei de Gauss para mostrar como as
cargas se distribuirão na parte interna e na parte externa da casca
esférica. R: (a)E=0; (b)E=q/(4pe0r2),
apontando para fora; (c)E=0; (d)E=q/(4pe0r2),
apontando para o centro da esfera.
 
Figura 3.5
Figura 3.6
|