Meu Mundo

Utilize g = 10 m/s² e p = 3 sempre que necessário na resolução das questões.

1. O famoso salto duplo twist carpado de Daiane dos Santos foi analisado durante um dia de treinamento no Centro Olímpico em Curitiba, através de sensores e filmagens que permitiram reproduzir a trajetória do centro de gravidade de Daiane na direção vertical (em metros), assim como o tempo de duração do salto. De acordo com o gráfico ao lado, determine:

a) A altura máxima atingida pelo centro de gravidade de Daiane.
Solução: Observando o gráfico, a altura máxima foi de 1,55 m. Resposta: 1,55 m.

b) A velocidade média horizontal do salto, sabendo-se que a distância percorrida nessa direção é de 1,3 m.
Solução: O tempo gasto foi de 1,1 segundo para percorrer 1,3m. Portanto, a velocidade média horizontal foi de v= 1,3/1,1 = 1,2 m/s.

c) A velocidade vertical de saída do solo.
Solução: Como o tempo para chegar ao ponto mais alto foi de 0,55 seg, a componente vertical no início do movimento foi de v_y² = 2gh Þ v_y² = 2.10.1,55 = 31 Þ v_y = 5,6 m/s. Resposta: 5,6 m/s.

2. No episódio II do filme Guerra nas Estrelas, um personagem mergulha em queda livre, caindo em uma nave que se deslocava horizontalmente a 100 m/s com os motores desligados. O personagem resgatado chegou à nave com uma velocidade de 6 m/s na vertical. Considere que a massa da nave é de 650 kg, a do personagem resgatado de 80 kg e a do piloto de 70 kg.

a) Quais as componentes horizontal e vertical da velocidade da nave imediatamente após o resgate?
Solução: De acordo com o princípio da conservação da quantidade de movimento:
(1) a componente vertical inicial da nave e do piloto é zero, portanto, em relação ao movimento vertical teremos:
Mr.v = (Mn + Mp + Mr)v’ Þ 80.6 = (650 + 80 + 70) v’ Þ v’ = 80.6/800 = 0,6 m/s.
(2) A componente horizontal inicial da nave e do piloto é 100 m/s e a do resgatado é zero.
(Mn + Mp).100 = (Mn + Mp + Mr).v’ Þ (650 +70).100 = (650 + 80 + 70) v’ Þ
Þ v’ = 720.100/800 = 90 m/s.
Resposta: a componente horizontal da velocidade será 90 m/s e a componente vertical da velocidade é 0,6 m/s.

b) Qual foi a variação da energia cinética total nesse resgate?
Solução:
Antes do resgate: (650 + 70).100²/2 + 80.6²/2 = 3601440J.
Após o regate, a velocidade do sistema será tal que V² = 0,6² + 90² = 8100,36.
A energia cinética é então: (Mn + Mp + Mr).V²/2 = 800. 8100,36/2 =3240144 J.
Isto corresponde a uma variação de 3240144 – 3601440 = -361296J. Resposta: -361296 J

3. Uma das aplicações mais comuns e bem sucedidas de alavancas são os alicates. Esse instrumento permite amplificar a força aplicada (Fa), seja para cortar (Fc), ou para segurar materiais pela ponta do alicate (Fp).

a) Um arame de aço tem uma resistência ao corte de 1,3 x 10⁹ N/m², ou seja, essa é a pressão mínima que deve ser exercida por uma lâmina para cortá-lo. Se a área de contato entre o arame e a lâmina de corte do alicate for de 0,1 mm², qual a força Fc necessária para iniciar o corte?

Solução: Como a resistência é de 1,3 x 10⁹ N/m² e a área é de 0,1 mm² = 0,1 x 10^-6 m², a força Fc necessária é Fc = 1,3 x 10⁹ . 1 x 10^-7 = 1,3 x 10² N. Resposta: 1,3 x 10² N

b) Se esse arame estivesse na região de corte do alicate a uma distância dc = 2 cm do eixo de rotação do alicate, que força Fa deveria ser aplicada para que o arame fosse cortado? (da = 10 cm)
Solução: A soma dos momentos em relação a qualquer ponto deve ser igual a zero.
Assim, Fc.dc – Fa.da = 0 Þ 1,3 x 10².2 = Fa.10 Þ Fa = 2,6 x 10¹ N. Resposta: 26 N.

4. Num conjunto arco e flecha, a energia potencial elástica é transformada em energia cinética da flecha durante o lançamento. A força da corda sobre a flecha é proporcional ao deslocamento x, como ilustrado na figura.

a) Quando a corda é solta, o deslocamento é x = 0,6 m e a força é de 300 N. Qual a energia potencial elástica nesse instante?
Solução: U = kx²/2 = Kx.x/2 = Fx/2 = 300.0,6/2 = 90 J. Resposta: 90 J.

b) Qual será a velocidade da flecha ao abandonar a corda? A massa da flecha é de 50 g. Despreze a resistência do ar e a massa da corda.
Solução: quando a flecha abandonar a corda, a energia potencial elástica é transformada em energia cinética da flecha.
Portanto, Mv²/2 = 90 onde M = 50 g = 50 x 10^-3 kg Þ v² = 90.2/50.10^-3 = 36 x 10² = = 6 x 10 = 60 m/s. Resposta: 60 m/s.

5. Em 1885, Michaux lançou o biciclo com uma roda dianteira diretamente acionada por pedais (Fig. A). Através do emprego da roda dentada, que já tinha sido concebida por Leonardo da Vinci, obteve-se melhor aproveitamento da força nos pedais (Fig. B). Considere que um ciclista consiga pedalar 40 voltas por minuto em ambas as bicicletas.

a) Qual a velocidade de translação do biciclo de Michaux para um diâmetro da roda de 1,20 m?
Solução: No caso da figura à esquerda, as velocidades angulares (e as freqüências) do pedal e da roda dianteira são iguais. Assim, v = 2pR_roda.f = 2.3.0,6.40 = 144 m/min = 144/60 = 2,4 m/s.

b) Qual a velocidade de translação para a bicicleta padrão aro 60 (Fig. B)?
Solução: na figura à direita as velocidades tangenciais do eixo da roda e da roda dentada são iguais. Assim, 2pR_eixof_eixo= 2pR_dentf_dent Þ 10f_eixo= 25.40 Þ f_eixo = 100 rpm.
A freqüência da rodada bicicleta é a mesma do eixo.
Portanto, v = 2pR_roda.f = 2.3.30.100 = 18000 cm/min = 180 m/min = 180 m/60s = 3 m/s. Resposta: 3 m/s.

6. Numa antena de rádio, cargas elétricas oscilam sob a ação de ondas eletromagnéticas em uma dada freqüência. Imagine que essas oscilações tivessem sua origem em forças mecânicas e não elétricas: cargas elétricas fixas em uma massa presa a uma mola. A amplitude do deslocamento dessa “antena-mola” seria de 1 mm e a massa de 1 g para um rádio portátil. Considere um sinal de rádio AM de 1000 kHz.

a) Qual seria a constante de mola dessa “antena-mola”? A freqüência de oscilação é dada por: f = (1/2p)(k/m)^1/2, onde k é a constante da mola e m a massa presa à mola.
Solução: São dados f = 1000 kHz = 10³.10³ Hz = 10⁶ Hz; m = 1 g = 10^-3 kg.
Da fórmula acima, k = f².m(2p)² = (10⁶)².10^-3.(2.3)² = 3,6 x 10¹⁰ N/m. Resposta: 3,6 x 10¹⁰ N/m.

b) Qual seria a força mecânica necessária para deslocar essa mola de 1 mm?
Solução: dados - k = 2,8 x 10⁷ N/m e x = 1 mm = 10^-3 m.
De F = kx resulta: F = 3,6 x 10¹⁰. 10^-3 = 3,6 x 10⁷ N. Resposta: 3,6 x 10⁷ N

7. Durante uma tempestade de 20 minutos, 10 mm de chuva caíram sobre uma região cuja área total é 100 km².

a) Sendo que a densidade da água é de 1,0 g/cm³, qual a massa de água que caiu?
Solução: expressando as medidas no SI temos:
20 minutos = 1200 segundos
10 mm = 10 x 10^-3 m = 1 x 10^-2 m
100 km² = 100x (10³)² = 1,0 x 10⁸ m².
1,0 g/cm3 = 1,0 x 10³ kg/m³.
Volume da água que caiu: V = A.h = 1,0 x 10⁸ . 1,0 x 10^-2 = 1,0 x 10⁶ m³.
Massa da água:m = V.d = 1,0 x10⁶ x 1,0 x 10³ = 1,0 x 10⁹ kg. Resposta: 1,0 x 10⁹ kg.

b) A partir de uma estimativa do volume de uma gota de chuva, calcule o número médio de gotas que caem em
1 m² durante 1 s.
Solução: considerando que em 1 cm³ existem 50 gotas, o volume de uma gota é 1/50 cm³ = 0,02 x (10-2)³ = 2 x 10^-8 m³.
O volume de chuva em 20 minutos= 20 x 60 = 1200 s, na área de 1m² é V = 1x0,01 = 0,01 m³ = 10^-2 m³. Portanto, em 1 s, o volume de água foi de 10^-2/1200 = 8,33 x10^-6 m³.
Portanto, é de se esperar cerca de 8,33 x 10-6 : 2,0 x 10^-8 = 4,2 x 10² gotas = 420 gotas. Resposta: 420 gotas.

8. Uma sala tem 6 m de largura, 10 m de comprimento e 4 m de altura. Deseja-se refrigerar o ar dentro da sala. Considere o calor específico do ar como sendo 30 J/ (mol.K) e use R = 8 J/(mol.K).

a) Considerando o ar dentro da sala como um gás ideal à pressão ambiente (P = 10⁵ N/m²), quantos moles de gás existem dentro da sala a 27 ºC?
Solução: São conhecidos - o volume V = 6.10.4 = 240 m3; a pressão P = 105 N/m2 e a temperatura T = 27ºC = 27 + 273 = 300 K.
Da equação dos gases perfeitos: PV = nRT Þ n = 10⁵ x 240/8.300 = 10⁴ moles. Resposta: 10⁴ moles.

b) Qual é a quantidade de calor que o refrigerador deve retirar da massa de ar do item (a) para resfriá-la até 17 ºC?
Solução: aplicando Q = nCDq, teremos Q = 104.30.(17 – 27) = - 3 x 10⁶ J.
Observação a variação da temperatura na escala Celsius e igual à variação da temperatura na escala Kelvin.
Resposta: 3 x 10⁶ J.

9. Um dos telescópios usados por Galileu por volta do ano de 1610 era composto de duas lentes convergentes, uma objetiva (lente 1) e uma ocular (lente 2) de distâncias focais iguais a 133 cm e 9,5 cm, respectivamente. Na observação de objetos celestes, a imagem (I1) formada pela objetiva situa-se praticamente no seu plano focal. Na figura (fora de escala), o raio R é proveniente da borda do disco lunar e o eixo óptico passa pelo centro da Lua.

a) A Lua tem 1.750 km de raio e fica a aproximadamente 384.000 km da Terra. Qual é o raio da imagem da Lua (I1) formada pela objetiva do telescópio de Galileu?
Solução: Se comparada a distância da lua em relação à distância focal da lente objetiva, pode-se considerar que sua imagem é formada sobre o foco dessa lente.
Assim, p’ = f que aplicado em i/O = p’/p resultará i/O = f/p.
Portanto: i/1750 = 133/384000 Þ i = 0,6 cm. (note que foi usada a razão cm/km). Resposta: 0,6 cm.

b) Uma segunda imagem (I₂) é formada pela ocular a partir daquela formada pela objetiva (a imagem da objetiva (I₁) torna-se objeto (O₂) para a ocular). Essa segunda imagem é virtual e situa-se a 20 cm da lente ocular. A que distância a ocular deve ficar da objetiva do telescópio para que isso ocorra?
Solução: da equação dos focos conjugados: 1/f = 1/p + 1/p’, temos: 1/(9,5) = 1/p + 1/(-20). Note a convenção de sinais: imagem virtual, pois é formada no mesmo lado que o objeto, p’ é negativo.
1/p = 1/9,5 + 1/20 Þ p’ = 9,5.20/(9,5 + 20) = 6,4 cm.
A distância da objetiva à ocular é então: 133 + 6,4 = 139,4 cm. Resposta: 139,4 cm.

10. O efeito fotoelétrico, cuja descrição por Albert Einstein está completando 100 anos em 2005 (ano internacional da Física), consiste na emissão de elétrons por um metal no qual incide um feixe de luz. No processo, “pacotes” bem definidos de energia luminosa, chamados fótons, são absorvidos um a um pelos elétrons do metal. O valor da energia de cada fóton é dado por Efóton = h f, onde h = 4 x 10^–15 eV.s é a chamada constante de Planck e f é a freqüência da luz incidente. Um elétron só é emitido do interior do metal se a energia do fóton absorvido for maior que uma energia mínima.
Para os elétrons mais fracamente ligados ao metal, essa energia mínima é chamada função trabalho W e varia de metal para metal (ver a tabela a seguir). Considere c = 300.000 km/s.

a) Calcule a energia do fóton (em eV), quando o comprimento de onda da luz incidente for 5 x 10^-7 m.
Solução: A energia de um fóton é determinada por E = hf = hc/l onde l é o comprimento de onda.
Temos h = 4 x 10^-15 eV.s, c = 300.000km/s = 3,0 x 10⁸ m/s, l = 5 x10^-7 m.
Assim, E = 4 x 10^–15.3 x 10⁸/5 x 10^-7 = 2,4 eV. Resposta: 2,4 eV.

b) A luz de 5 x 10^-7 m é capaz de arrancar elétrons de quais dos metais apresentados na tabela?
Solução: a tabela mostra a energia de ligação dos elétrons ao átomo. Para arrancar o elétron, o fóton deve
apresentar energia superior à energia de ligação. Portanto, serão arrancados elétrons do césio e do potássio.
Resposta: césio e potássio.

c) Qual será a energia cinética de elétrons emitidos pelo potássio, se o comprimento de onda da luz incidente for
3 x 10^-7 m? Considere os elétrons mais fracamente ligados do potássio e que a diferença entre a energia do fóton absorvido e a função trabalho W é inteiramente convertida em energia cinética.
Solução: a energia do elétron emitido será Ec = hf – W = hc/l.
Para fótons de comprimento de onda 3 x 10-7 m,
Ec = 4 x 10^–15.3 x 10⁸/3 x 10^-7 – 2,3 = 4 - 2,3 = 1,7 eV. Resposta: 1,7 eV.

11. O princípio de funcionamento dos detectores de metais utilizados em verificações de segurança é baseado na lei de indução de Faraday. A força eletromotriz induzida por um fluxo de campo magnético variável através de uma espira gera uma corrente. Se um pedaço de metal for colocado nas proximidades da espira, o valor do campo magnético será alterado, modificando a corrente na espira. Essa variação pode ser detectada e usada para reconhecer a presença de um corpo metálico nas suas vizinhanças.

a) Considere que o campo magnético B atravessa perpendicularmente a espira e varia no tempo segundo a figura. Se a espira tem raio de 2 cm, qual é a força eletromotriz induzida?

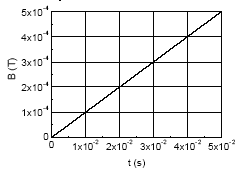
Solução: De acordo com a lei de Lenz, a força eletromotriz é igual à variação do fluxo magnético por unidade de tempo. Assim, e = Dj/Dt = (DB).A/Dt = (B_f – B₀).A/(t_f – t₀).
Pelo gráfico: B_f= 5 x 10^-4 tesla; B₀ = 0; t_f = 5 x10^-2 s; t₀ = 0.
Como a espira tem raio 2 cm = 2x10^-2 m, sua área é A = p.r² = 3.(2x10^-2)² = 12x10^-4 m².
Assim, e = (5x10^-5 – 0).12x10^-4/(5x10^-2 – 0) = 1,2 x 10^-6 V. Resposta: 1,2 x 10^-6 V.

b) A espira é feita de um fio de cobre de 1 mm de raio e a resistividade do cobre é r = 2 x 10^-8 ohm-metro. A resistência de um fio é dada por R = rL/A, onde L é o seu comprimento e A é a área da sua seção reta. Qual é a corrente na espira?
Solução: comprimento da espira: L = 2.pR = 2.3.2x10^-2 = 12x10^-2 m.
Área da seção transversal do fio da espira A = pr² = 3. (1mm)² = 3.(10^-3 m)² = 3 x 10^-6 m².
Deste modo, R = rL/A = 2 x 10^-8.12x10^-2/(3 x 10^-6) = 8 x 10^-4 ohms.
A corrente é i = e/R = 8 x 10^-7.3 x 10^-6/16 x 10^-4 = 1,5 x 10^-4 A. Resposta: 1,5x10^-4A.

12. A durabilidade dos alimentos é aumentada por meio de tratamentos térmicos, como no caso do leite longa vida. Esses processos térmicos matam os microorganismos, mas provocam efeitos colaterais indesejáveis. Um dos métodos alternativos é o que utiliza campos elétricos pulsados, provocando a variação de potencial através da célula, como ilustrado na figura abaixo. A membrana da célula de um microorganismo é destruída se uma diferença de potencial de DV_m = 1 V é estabelecida no interior da membrana, conforme a figura abaixo .

a) Sabendo-se que o diâmetro de uma célula é de 1µm, qual é a intensidade do campo elétrico que precisa ser aplicado para destruir a membrana?
Solução: De acordo com o gráfico a diferença de potencial entre a membrana à direita e a membrana à esquerda é 2. DV_m = 2.1 = 2 V.

De E = DV/d = 2 V/(1µm) = 2V/(10^-6m) = 2.10⁶ V/m ou 2.10⁶N?C. Resposta: 2.10⁶ V/m.

b) Qual é o ganho de energia em eV de um elétron que atravessa a célula sob a tensão aplicada?
Solução: a energia ganha é U = q.DV = 1e.2V = 2 eV. Resposta: 2 eV.

Resolvido e editado por Cesário José Ferreira