O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça corresponder a todo elemento do primeiro conjunto um único elemento do segundo, ocorre uma função.

O uso de funções pode ser encontrado em diversos assuntos. Por exemplo, na tabela de preços de uma loja, a cada produto corresponde um determinado preço. Outro exemplo seria o preço a ser pago numa conta de luz, que depende da quantidade de energia consumida.

Observe, por exemplo, o diagrama das relações abaixo:

A relação acima não é uma função, pois existe o elemento 1 no conjunto A, que não está associado a nenhum elemento do conjunto B.

A relação acima também não é uma função, pois existe o elemento 4 no conjunto A, que está associado a mais de um elemento do conjunto B.

Agora preste atenção no próximo exemplo:

A relação acima é uma função, pois todo elemento do conjunto A, está associado a somente um elemento do conjunto B.

O domínio de uma função é sempre o próprio conjunto de partida, ou seja, D=A. Se um elemento x Î A estiver associado a um elemento y Î B, dizemos que y é a imagem de x (indica-se y=f(x) e lê-se "y é igual a f de x").

Exemplo: se f é uma função de IN em IN (isto significa que o domínio e o contradomínio são os números naturais) definida por y=x+2. Então temos que:

• A imagem de 1 através de f é 3, ou seja, f(1)=1+2=3;
• A imagem de 2 através de f é 4, ou seja, f(2)=2+2=4;

De modo geral, a imagem de x através de f é x+2, ou seja: f(x)=x+2.

Numa função f de A em B, os elementos de B que são imagens dos elementos de A através da aplicação de f formam o conjunto imagem de f.

Com base nos diagramas acima, concluímos que existem 2 condições para uma relação f seja uma função:

Observações:

• Como x e y têm seus valores variando nos conjuntos A e B, recebem o nome de variáveis.
• A variável x é chamada variável independente e a variável y, variável dependente, pois para obter o valor de y dependemos de um valor de x.
• Uma função f fica definida quando são dados seu domínio (conjunto A), seu contradomínio (conjunto B) e a lei de associação y=f(x).

1. Considere a função f: A à B representada pelo diagrama a seguir:

1. o domínio (D) de f;
2. f(1), f(-3), f(3) e f(2);
3. o conjunto imagem (Im) de f;
4. a lei de associção

1. O domínio é igual ao conjunto de partida, ou seja, D=A.
2. f(1)=1, f(-3)=9, f(3)=9 e f(2)=4.
3. O conjunto imagem é formado por todas imagens dos elementos do domínio, portanto: Im = {1,4,9}.
4. Como 1²=1, (-3)²=9, 3²=9 e 2²=4, temos y=x².

1. Dada a função f: IRà IR (ou seja, o domínio e a contradomínio são os números reais) definida por f(x)=x²-5x+6, calcule:

1. f(2), f(3) e f(0);
2. o valor de x cuja imagem vale 2.

1. f(2)= 2²-5(2)+6 = 4-10+6 = 0

f(3)= 3²-5(3)+6 = 9-15+6 = 0

f(0)= 0²-5(0)+6 = 0-0+6 = 6

2. Calcular o valor de x cuja imagem vale 2 equivale a resolver a equação f(x)=2, ou seja, x²-5x+6=2. Utilizando a fórmula de Bhaskara encontramos as raízes 1 e 4. Portanto os valores de x que têm imagem 2 são 1 e 4.

• O domínio é o subconjunto de IR no qual todas as operações indicadas em y=f(x) são possíveis.

Para construir o gráfico de uma função f, basta atribuir valores do domínio à variável x e, usando a sentença matemática que define a função, calcular os correspondentes valores da variável y. Por exemplo, vamos construir o gráfico da função definida por y=x/2. Escolhemos alguns valores para o domínio. Por exemplo D={2,4,6,8}, e agora calculamos os respectivos valores de y. Assim temos:

Identificamos os pontos encontrados no plano cartesiano:

O gráfico da função será uma reta que passará pelos quatro pontos encontrados. Basta traçar a reta, e o gráfico estará construído.

Obs: para desenhar o gráfico de uma reta são necessários apenas dois pontos. No exemplo acima escolhemos 4 pontos, mas bastaria escolher dois elementos do domínio, encontrar suas imagens, e logo após traçar a reta que passa por esses 2 pontos.

Dada uma função y=f(x), os valores, os valores de x para os quais f(x)=0 são chamados raízes de uma função. No gráfico cartesiano da função, as raízes são abscissas dos pontos onde o gráfico corta o eixo horizontal. Observe o gráfico abaixo:

No gráfico acima temos: f(x₁)=0, f(x₂)=0 e f(x₃)=0.

Portanto x₁, x₂ e x₃ são raízes da função.

Essas são algumas propriedades que caracterizam uma função f:Aà B:

1. Função sobrejetora: Dizemos que uma função é sobrejetora se, e somente se, o seu conjunto imagem for igual ao contradomínio, isto é, se Im=B. Em outras palavras, não pode sobrar elementos no conjunto B sem receber flechas.
2. Função Injetora: A função é injetora se elementos distintos do domínio tiverem imagens distintas, ou seja, dois elementos não podem ter a mesma imagem. Portanto não pode haver nenhum elemento no conjunto B que receba duas flechas. Por exemplo, a função f:IRà IR definida por f(x)=3x é injetora pois se x₁ ¹ x₂ então 3x₁ ¹ 3x₂, portanto f(x₁)¹ f(x₂).
3. Função Bijetora: Uma função é bijetora quando ela é sobrejetora e injetora ao mesmo tempo. Por exemplo, a função f: IRà IR definida por y=3x é injetora, como vimos no exemplo anterior. Ela também é sobrejetora, pois Im=B=IR. Logo, esta função é bijetora.

Dada uma função f: Aà B, dizemos que f é par se, e somente se, f(x)=f(-x) para todo x Î A. Ou seja: os valores simétricos devem possuir a mesma imagem. O diagrama a seguir mostra um exemplo de função par:

Por exemplo, a função f: IRà IR definida por f(x)=x² é uma função par, pois f(x)=x²=(-x)²=f(-x). Podemos notar a paridade dessa função observando o seu gráfico:

Notamos, no gráfico, que existe uma simetria em relação ao eixo vertical. Elementos simétricos têm a mesma imagem. Os elementos 2 e –2, por exemplo, são simétricos e possuem a imagem 4.

Por outro lado, dada uma função f: Aà B, dizemos que f é ímpar se, e somente se, f(-x)=-f(x) para todo x Î A. Ou seja: valores simétricos possuem imagens simétricas. O diagrama a seguir mostra um exemplo de função ímpar:

Por exemplo, a função f: IRà IR definida por f(x)=x³ é uma função ímpar, pois f(-x)=(-x)³=-x³=-f(x). Podemos notar que a função é ímpar observando o seu gráfico:

Notamos, no gráfico, que existe uma simetria em relação a origem 0. Elementos simétricos têm imagens simétricas. Os elementos 1 e –1, por exemplo, são simétricos e possuem imagens 1 e –1 (que também são simétricas).

Obs: Uma função que não é par nem ímpar é chamada função sem paridade.

1. Classifique as funções abaixo em pares, ímpares ou sem paridade:

1. f(x)=2x

f(-x)= 2(-x) = -2x è f(-x) = -f(x), portanto f é ímpar.

Dada uma função f: Aà B, dizemos que f é crescente em algum conjunto A’ Ì A, se, e somente se, para quaisquer x₁ Î A’ e x₂ Î A’, com x₁<x₂, tivermos f(x₁)<f(x₂).

Por exemplo, a função f:IRà IR definida por f(x)=x+1 é crescente em IR, pois x₁<x₂ => x₁+1<x₂+1 => f(x₁)<f(x₂). Ou seja: quando os valores do domínio crescem, suas imagens também crescem.

Por outro lado, dada uma função f: Aà B, dizemos que f é decrescente em algum conjunto A’ Ì A, se, e somente se, para quaisquer x₁ Î A’ e x₂ Î A’, com x₁<x₂, tivermos f(x₁)>f(x₂).

Por exemplo, a função f:IRà IR definida por f(x)= -x+1 é decrescente em IR, pois x₁<x₂ => -x₁>-x₂ => -x₁+1>-x₂+1 => f(x₁)>f(x₂). Ou seja: quando os valores do domínio crescem, suas correspondentes imagens decrescem.

Vamos analisar um exemplo para entender o que é uma função composta.

Consideremos os conjuntos A={-2,-1,0,1,2}, B={-2,1,4,7,10} e C={3,0,15,48,99}, e as funções f:Aà B definida por f(x)=3x+4, e g:Bà C definida por g(y)=y²-1.

Como nos mostra o diagrama acima, para todo x Î A temos um único y Î B tal que y=3x+4, e para todo y Î B existe um único z Î C tal que z=y²-1, então concluímos que existe uma função h de A em C, definida por h(x)=z ou h(x)=9x²+24x+15, pois:

h(x)=z è h(x)= y²-1

E sendo y=3x+4, então h(x)=(3x+4)²-1 è h(x)= 9x²+24x+15.

A função h(x) é chamada função composta de g com f. Podemos indicá-la por g o f (lemos "g composta com f") ou g[f(x)] (lemos "g de f de x"). Vamos ver alguns exercícios para entender melhor a idéia de função composta.

1. Dadas as funções f(x)=x²-1 e g(x)=2x, calcule f[g(x)] e g[f(x)].

Resolução:

f[g(x)] = f(2x) = (2x)²-1 = 4x²-1

g[f(x)] = g(x²-1) = 2(x²-1) = 2x²-2

2. Dadas as funções f(x)=5x e f[g(x)]=3x+2, calcule g(x).

Resolução:

Como f(x)=5x, então f[g(x)]= 5.g(x).

Porém, f[g(x)]=3x+2; logo 5.g(x)=3x+2, e daí g(x)=(3x+2)/5

3. Dadas as funções f(x)=x²+1 e g(x)=3x-4, determine f[g(3)].

A função f é uma função bijetora. A cada elemento x de A está associado um único elemento y de B, de modo que y=x+1.

Porém, como f é bijetora, a cada elemento y de B está associado um único elemento x de A, de modo que x=y-1; portanto temos uma outra função g:Bà A, de modo que x=y-1 ou g(y)=y-1. Essa função está representada no diagrama abaixo:

Pelo que acabamos de ver, a função f leva x até y enquanto a função g leva y até x. A função g:Bà A recebe o nome de função inversa de f e é indicada por f^-1.

O domínio de f é o conjunto imagem de g, e o conjunto imagem de f é o domínio de g. Quando queremos, a partir da sentença y=f(x), obter a sentença de f^-1(x), devemos dar os seguintes passos:

1º) Isolamos x na sentença y=f(x)

2º) Pelo fato de ser usual a letra x como símbolo da variável independente, trocamos x por y e y por x.

Por exemplo, para obter a função inversa de f:IRà IR definida por y=2x+1, devemos:

1º) isolar x em y=2x+1. Assim y=2x+1 è y-1=2x è x=(y-1)/2

2º) trocar x por y e y por x: y=(x-1)/2.

Portanto a função inversa de f é: f^-1(x)=(x-1)/2.

Observação: Para que uma função f admita a inversa f^-1 é necessário que ela seja bijetora. Se f não for bijetora, ela não possuirá inversa.

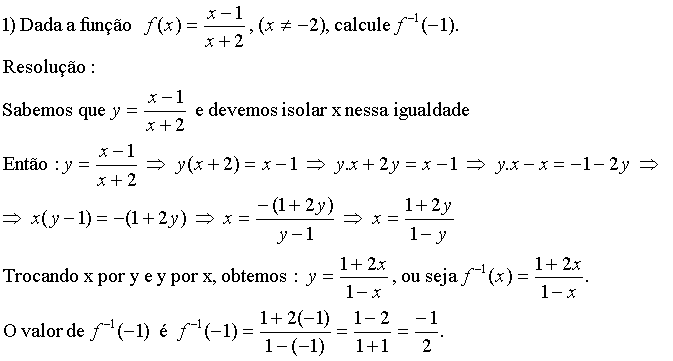
Esse documento foi criado por Juliano Zambom Niederauer.

Os gráficos e diagramas utilizados no documento foram retirados do livro: