..... FUNÇÂO INVERSA

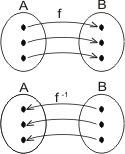
..... Se f: A B é uma função bijetora, então existe uma única função g: B => A, tal que g(b) = a f(a) = b para todo a A e b B. A função g é chamada inversa de f e será indicada por f -1. assim:

Para obtermos a função inversa de uma função f(x), devemos:
1) na função y = f(x), trocar x por y e y por x;
2) em seguida, isolar y, obtendo f -1(x).

Observações:

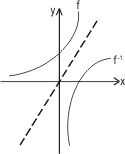
1. Os gráficos de f e f -1 são simétricos em relação à bissetriz do 1º e 3º quadrantes.

2. fo f -1(x) = fo-1 f(x) = x.

Exemplo:

Determine a inversa da função

y = __x__
..... 2x + 4

Resolução:

Trocando x por y e y por x, temos:

x = __y__
......2y + 4

Isolando a variável y:

x = __y__ x(2y + 4) = 2xy 2xy + 4 x = y
......2y + 4

4x = y – 2xy 4x = y(1 – 2x) __4x__ = y
..........................................................1 – 2x

Assim, a inversa da função f(x) = __x__ é a função f –1(x) = __4x__
...................................................2 + 4x ................................1 – 2x

Aula Anterior .................................. Matemática 1 ..............................................Pròxima Aula