Teoría sobre Óptica Geométrica.

	Hacé click sobre el ítem teórico que quieras ver.

Óptica, rama de la física que se ocupa de la propagación y el comportamiento de la luz. En un sentido amplio, la luz es la zona del espectro de radiación electromagnética que se extiende desde los rayos X hasta las microondas, e incluye la energía radiante que produce la sensación de visión. El estudio de la óptica se divide en dos ramas, la óptica geométrica y la óptica física. En esta página nos ocuparemos solo de la primera.

Naturaleza de la luz

La energía radiante tiene una naturaleza dual, y obedece leyes que pueden explicarse a partir de una corriente de partículas o paquetes de energía, los llamados fotones, o a partir de un tren de ondas transversales. El concepto de fotón se emplea para explicar las interacciones de la luz con la materia que producen un cambio en la forma de energía, como ocurre con el efecto fotoeléctrico o la luminiscencia. El concepto de onda suele emplearse para explicar la propagación de la luz y algunos de los fenómenos de formación de imágenes. En las ondas de luz, como en todas las ondas electromagnéticas, existen campos eléctricos y magnéticos en cada punto del espacio, que fluctúan con rapidez. Como estos campos tienen, además de una magnitud, una dirección determinada, son cantidades vectoriales. Los campos eléctrico y magnético son perpendiculares entre sí y también perpendiculares a la dirección de propagación de la onda. La onda luminosa más sencilla es una onda sinusoidal pura, llamada así porque una gráfica de la intensidad del campo eléctrico o magnético trazada en cualquier momento a lo largo de la dirección de propagación sería la gráfica de una función seno. El número de oscilaciones o vibraciones por segundo en un punto de la onda luminosa se conoce como frecuencia. La longitud de onda es la distancia a lo largo de la dirección de propagación entre dos puntos con la misma ‘fase’, es decir, puntos que ocupan posiciones equivalentes en la onda. Por ejemplo, la longitud de onda es igual a la distancia que va de un máximo de la onda sinusoidal a otro, o de un mínimo a otro. En el espectro visible, las diferencias en longitud de onda se manifiestan como diferencias de color. El rango visible va desde 350 nanómetros (violeta) hasta 750 nanómetros (rojo), aproximadamente (un nanómetro, nm, es una milmillonésima de metro). La luz blanca es una mezcla de todas las longitudes de onda visibles. No existen límites definidos entre las diferentes longitudes de onda, pero puede considerarse que la radiación ultravioleta va desde los 350 nm hasta los 10 nm. Los rayos infrarrojos, que incluyen la energía calorífica radiante, abarcan las longitudes de onda situadas aproximadamente entre 750 nm y 1 mm. La velocidad de una onda electromagnética es el producto de su frecuencia y su longitud de onda. En el vacío, la velocidad es la misma para todas las longitudes de onda. La velocidad de la luz en las sustancias materiales es menor que en el vacío, y varía para las distintas longitudes de onda; este efecto se denomina dispersión. La relación entre la velocidad de la luz en el vacío y la velocidad de una longitud de onda determinada en una sustancia se conoce como índice de refracción de la sustancia para dicha longitud de onda. El índice de refracción del aire es 1,00029 y apenas varía con la longitud de onda. En la mayoría de las aplicaciones resulta suficientemente preciso considerar que es igual a 1.

Las leyes de reflexión y refracción de la luz suelen deducirse empleando la teoría ondulatoria de la luz introducida en el siglo XVII por el matemático, astrónomo y físico holandés Christiaan Huygens. El principio de Huygens afirma que todo punto de un frente de onda inicial puede considerarse como una fuente de ondas esféricas secundarias que se extienden en todas las direcciones con la misma velocidad, frecuencia y longitud de onda que el frente de onda del que proceden. Con ello puede definirse un nuevo frente de onda que envuelve las ondas secundarias. Como la luz avanza en ángulo recto a este frente de onda, el principio de Huygens puede emplearse para deducir los cambios de dirección de la luz.

Cuando las ondas secundarias llegan a otro medio u objeto, cada punto del límite entre los medios se convierte en una fuente de dos conjuntos de ondas. El conjunto reflejado vuelve al primer medio, y el conjunto refractado entra en el segundo medio. El comportamiento de los rayos reflejados y refractados puede explicarse por el principio de Huygens. Es más sencillo, y a veces suficiente, representar la propagación de la luz mediante rayos en vez de ondas. El rayo es la línea de avance, o dirección de propagación, de la energía radiante y, por tanto, perpendicular al frente de onda. En la óptica geométrica se prescinde de la teoría ondulatoria de la luz y se supone que la luz no se difracta. La trayectoria de los rayos a través de un sistema óptico se determina aplicando las leyes de reflexión y refracción.

(volver arriba)

Óptica geométrica

Este campo de la óptica se ocupa de la aplicación de las leyes de reflexión y refracción de la luz al diseño de lentes y otros componentes de instrumentos ópticos.

Reflexión y refracción

Refracción de la luz en diamantes El brillo de los diamantes se debe a su elevado índice de refracción, aproximadamente 2,4. El índice de refracción de un material transparente indica cuánto desvía los rayos de luz. La habilidad del joyero reside en tallar las facetas de modo que cada rayo de luz se refleje muchas veces antes de salir de la piedra. El índice de refracción es ligeramente distinto para cada color de la luz, por lo que la luz blanca se divide en sus componentes dando lugar a los fuegos multicolores de los diamantes.

Si un rayo de luz que se propaga a través de un medio homogéneo incide sobre la superficie de un segundo medio homogéneo, parte de la luz es reflejada y parte entra como rayo refractado en el segundo medio, donde puede o no ser absorbido. La cantidad de luz reflejada depende de la relación entre los índices de refracción de ambos medios. El plano de incidencia se define como el plano formado por el rayo incidente y la normal (es decir, la línea perpendicular a la superficie del medio) en el punto de incidencia (véase figura 1). El ángulo de incidencia es el ángulo entre el rayo incidente y la normal. Los ángulos de reflexión y refracción se definen de modo análogo.

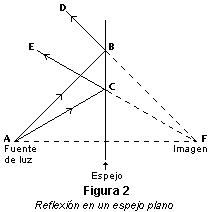
Las leyes de la reflexión afirman que el ángulo de incidencia es igual al ángulo de reflexión, y que el rayo incidente, el rayo reflejado y la normal en el punto de incidencia se encuentran en un mismo plano. Si la superficie del segundo medio es lisa, puede actuar como un espejo y producir una imagen reflejada (figura 2). En la figura 2, la fuente de luz es el objeto A; un punto de A emite rayos en todas las direcciones. Los dos rayos que inciden sobre el espejo en B y C, por ejemplo, se reflejan como rayos BD y CE. Para un observador situado delante del espejo, esos rayos parecen venir del punto F que está detrás del espejo. De las leyes de reflexión se deduce que CF y BF forman el mismo ángulo con la superficie del espejo que AC y AB. En este caso, en el que el espejo es plano, la imagen del objeto parece situada detrás del espejo y separada de él por la misma distancia que hay entre éste y el objeto que está delante.

Si la superficie del segundo medio es rugosa, las normales a los distintos puntos de la superficie se encuentran en direcciones aleatorias. En ese caso, los rayos que se encuentren en el mismo plano al salir de una fuente puntual de luz tendrán un plano de incidencia, y por tanto de reflexión, aleatorio. Esto hace que se dispersen y no puedan formar una imagen.

(volver arriba)

Ley de Snell

Esta importante ley, llamada así en honor del matemático holandés Willebrord van Roijen Snell, afirma que el producto del índice de refracción del primer medio y el seno del ángulo de incidencia de un rayo es igual al producto del índice de refracción del segundo medio y el seno del ángulo de refracción. El rayo incidente, el rayo refractado y la normal a la superficie de separación de los medios en el punto de incidencia están en un mismo plano. En general, el índice de refracción de una sustancia transparente más densa es mayor que el de un material menos denso, es decir, la velocidad de la luz es menor en la sustancia de mayor densidad. Por tanto, si un rayo incide de forma oblicua sobre un medio con un índice de refracción mayor, se desviará hacia la normal, mientras que si incide sobre un medio con un índice de refracción menor, se desviará alejándose de ella. Los rayos que inciden en la dirección de la normal son reflejados y refractados en esa misma dirección.

Ley de Snell: n1 sen i = n2 sen r

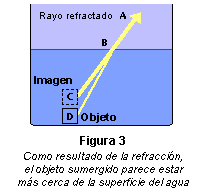
Para un observador situado en un medio menos denso, como el aire, un objeto situado en un medio más denso parece estar más cerca de la superficie de separación de lo que está en realidad. Un ejemplo habitual es el de un objeto sumergido, observado desde encima del agua, como se muestra en la figura 3 (sólo se representan rayos oblicuos para ilustrar el fenómeno con más claridad). El rayo DB procedente del punto D del objeto se desvía alejándose de la normal, hacia el punto A. Por ello, el objeto parece situado en C, donde la línea ABC intersecta una línea perpendicular a la superficie del agua y que pasa por D.

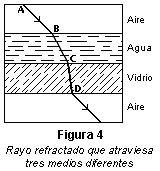
En la figura 4 se muestra la trayectoria de un rayo de luz que atraviesa varios medios con superficies de separación paralelas. El índice de refracción del agua es más bajo que el del vidrio. Como el índice de refracción del primer y el último medio es el mismo, el rayo emerge en dirección paralela al rayo incidente AB, pero resulta desplazado.

(volver arriba)

Prismas

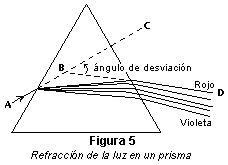
Cuando la luz atraviesa un prisma —un objeto transparente con superficies planas y pulidas no paralelas—, el rayo de salida ya no es paralelo al rayo incidente. Como el índice de refracción de una sustancia varía según la longitud de onda, un prisma puede separar las diferentes longitudes de onda contenidas en un haz incidente y formar un espectro. En la figura 5, el ángulo CBD entre la trayectoria del rayo incidente y la trayectoria del rayo emergente es el ángulo de desviación. Puede demostrarse que cuando el ángulo de incidencia es igual al ángulo formado por el rayo emergente, la desviación es mínima. El índice de refracción de un prisma puede calcularse midiendo el ángulo de desviación mínima y el ángulo que forman las caras del prisma.

Prisma - Leyes

(volver arriba)

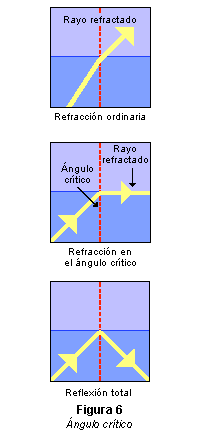
Ángulo crítico

Puesto que los rayos se alejan de la normal cuando entran en un medio menos denso, y la desviación de la normal aumenta a medida que aumenta el ángulo de incidencia, hay un determinado ángulo de incidencia, denominado ángulo crítico, para el que el rayo refractado forma un ángulo de 90°. Con la normal, por lo que avanza justo a lo largo de la superficie de separación entre ambos medios. Si el ángulo de incidencia se hace mayor que el ángulo crítico, los rayos de luz serán totalmente reflejados. La reflexión total no puede producirse cuando la luz pasa de un medio menos denso a otro más denso. Las tres ilustraciones de la figura 6 muestran la refracción ordinaria, la refracción en el ángulo crítico y la reflexión total.

La fibra óptica es una nueva aplicación práctica de la reflexión total. Cuando la luz entra por un extremo de un tubo macizo de vidrio o plástico, puede verse reflejada totalmente en la superficie exterior del tubo y, después de una serie de reflexiones totales sucesivas, salir por el otro extremo. Es posible fabricar fibras de vidrio de diámetro muy pequeño, recubrirlas con un material de índice de refracción menor y juntarlas en haces flexibles o placas rígidas que se utilizan para transmitir imágenes. Los haces flexibles, que pueden emplearse para iluminar además de para transmitir imágenes, son muy útiles para la exploración médica, ya que pueden introducirse en cavidades estrechas e incluso en vasos sanguíneos.

(volver arriba)

Superficies esféricas y asféricas

La mayor parte de la terminología tradicional de la óptica geométrica se desarrolló en relación con superficies esféricas de reflexión y refracción. Sin embargo, a veces se consideran superficies no esféricas o asféricas. El eje óptico es una línea de referencia que constituye un eje de simetría, y pasa por el centro de una lente o espejo esféricos y por su centro de curvatura. Si un haz de rayos estrecho que se propaga en la dirección del eje óptico incide sobre la superficie esférica de un espejo o una lente delgada, los rayos se reflejan o refractan de forma que se cortan, o parecen cortarse, en un punto situado sobre el eje óptico. La distancia entre ese punto (llamado foco) y el espejo o lente se denomina distancia focal. Cuando una lente es gruesa, los cálculos se realizan refiriéndolos a unos planos denominados planos principales, y no a la superficie real de la lente. Si las dos superficies de una lente no son iguales, ésta puede tener dos distancias focales, según cuál sea la superficie sobre la que incide la luz. Cuando un objeto está situado en el foco, los rayos que salen de él serán paralelos al eje óptico después de ser reflejados o refractados. Si una lente o espejo hace converger los rayos de forma que se corten delante de dicha lente o espejo, la imagen será real e invertida. Si los rayos divergen después de la reflexión o refracción de modo que parecen venir de un punto por el que no han pasado realmente, la imagen no está invertida y se denomina imagen virtual. La relación entre la altura de la imagen y la altura del objeto se denomina aumento lateral.

Si se consideran positivas las distancias del eje x medidas desde una lente o espejo en el sentido contrario a la luz incidente contado a partir del vértice. Eje +y hacia arriba, entonces, siendo u la distancia del objeto, v la distancia de la imagen y f la distancia focal de un espejo o una lente delgada, los espejos esféricos cumplen la ecuación

1/u + 1/v = 1/f

y las lentes esféricas la ecuación

1/u - 1/v = 1/f

Si llamamos y al tamaño del objeto e y' al de la imágen, entonces para el agrandamiento la expresión será la siguiente:

A = y'/y

Si una lente simple tiene superficies de radios r 1 y r 2 y la relación entre su índice de refracción y el del medio que la rodea es n, se cumple que

La distancia focal de un espejo esférico es igual a la mitad de su radio de curvatura. Como se indica en la figura 7, los rayos que se desplazan en un haz estrecho en la dirección del eje óptico e inciden sobre un espejo cóncavo cuyo centro de curvatura está situado en C, se reflejan de modo que se cortan en B, a media distancia entre A y C. Si la distancia del objeto es mayor que la distancia AC, la imagen es real, reducida e invertida. Si el objeto se encuentra entre el centro de curvatura y el foco, la imagen es real, aumentada e invertida. Si el objeto está situado entre la superficie del espejo y su foco, la imagen es virtual, aumentada y no invertida. Un espejo convexo sólo forma imágenes virtuales, reducidas y no invertidas, a no ser que se utilice junto con otros componentes ópticos.

(volver arriba)

Lentes

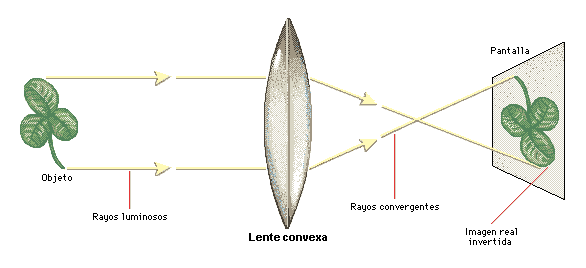Lente convexa. Una lente convexa es más gruesa en el centro que en los extremos. La luz que atraviesa una lente convexa se desvía hacia dentro (converge). Esto hace que se forme una imagen del objeto en una pantalla situada al otro lado de la lente. La imagen está enfocada si la pantalla se coloca a una distancia determinada, que depende de la distancia del objeto y del foco de la lente. La lente del ojo humano es convexa, y además puede cambiar de forma para enfocar objetos a distintas distancias. La lente se hace más gruesa al mirar objetos cercanos y más delgada al mirar objetos lejanos. A veces, los músculos del ojo no pueden enfocar la luz sobre la retina, la pantalla del globo ocular. Si la imagen de los objetos cercanos se forma detrás de la retina, se dice que existe hipermetropía.

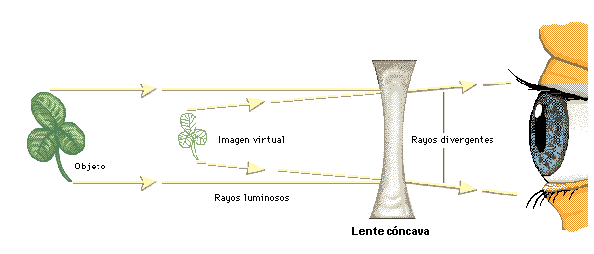
Lente cóncava. Las lentes cóncavas están curvadas hacia dentro. La luz que atraviesa una lente cóncava se desvía hacia fuera (diverge). A diferencia de las lentes convexas, que producen imágenes reales, las cóncavas sólo producen imágenes virtuales, es decir, imágenes de las que parecen proceder los rayos de luz. En este caso es una imagen más pequeña situada delante del objeto (el trébol). En las gafas o anteojos para miopes, las lentes cóncavas hacen que los ojos formen una imagen nítida en la retina y no delante de ella.

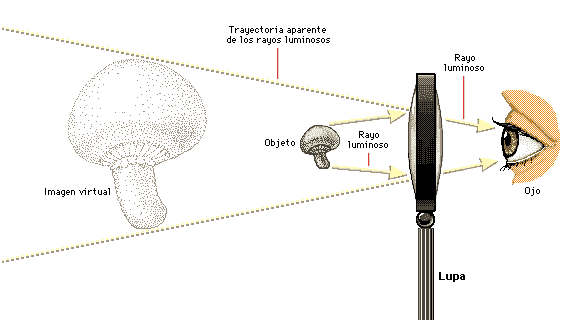
Lupa. Una lupa es una lente convexa grande empleada para examinar objetos pequeños. La lente desvía la luz incidente de modo que se forma una imagen virtual ampliada del objeto (en este caso un hongo) por detrás del mismo. La imagen se llama virtual porque los rayos que parecen venir de ella no pasan realmente por ella. Una imagen virtual no se puede proyectar en una pantalla.

Las lentes con superficies de radios de curvatura pequeños tienen distancias focales cortas. Una lente con dos superficies convexas siempre refractará los rayos paralelos al eje óptico de forma que converjan en un foco situado en el lado de la lente opuesto al objeto. Una superficie de lente cóncava desvía los rayos incidentes paralelos al eje de forma divergente; a no ser que la segunda superficie sea convexa y tenga una curvatura mayor que la primera, los rayos divergen al salir de la lente, y parecen provenir de un punto situado en el mismo lado de la lente que el objeto. Estas lentes sólo forman imágenes virtuales, reducidas y no invertidas.

Si la distancia del objeto es mayor que la distancia focal, una lente convergente forma una imagen real e invertida. Si el objeto está lo bastante alejado, la imagen será más pequeña que el objeto. Si la distancia del objeto es menor que la distancia focal de la lente, la imagen será virtual, mayor que el objeto y no invertida. En ese caso, el observador estará utilizando la lente como una lupa o microscopio simple. El ángulo que forma en el ojo esta imagen virtual aumentada (es decir, su dimensión angular aparente) es mayor que el ángulo que formaría el objeto si se encontrara a la distancia normal de visión. La relación de estos dos ángulos es la potencia de aumento de la lente. Una lente con una distancia focal más corta crearía una imagen virtual que formaría un ángulo mayor, por lo que su potencia de aumento sería mayor. La potencia de aumento de un sistema óptico indica cuánto parece acercar el objeto al ojo,y es diferente del aumento lateral de una cámara o telescopio, por ejemplo, donde la relación entre las dimensiones reales de la imagen real y las del objeto aumenta según aumenta la distancia focal.

La cantidad de luz que puede admitir una lente aumenta con su diámetro. Como la superficie que ocupa una imagen es proporcional al cuadrado de la distancia focal de la lente, la intensidad luminosa de la superficie de la imagen es directamente proporcional al diámetro de la lente e inversamente proporcional al cuadrado de la distancia focal. Por ejemplo, la imagen producida por una lente de 3 cm de diámetro y una distancia focal de 20 cm sería cuatro veces menos luminosa que la formada por una lente del mismo diámetro con una distancia focal de 10 cm. La relación entre la distancia focal y el diámetro efectivo de una lente es su relación focal, llamada también número f. Su inversa se conoce como abertura relativa. Dos lentes con la misma abertura relativa tienen la misma luminosidad, independientemente de sus diámetros y distancias focales.

(volver arriba)

Aberración

La óptica geométrica predice que la imagen de un punto formada por elementos ópticos esféricos no es un punto perfecto, sino una pequeña mancha. Las partes exteriores de una superficie esférica tienen una distancia focal distinta a la de la zona central, y este defecto hace que la imagen de un punto sea un pequeño círculo. La diferencia en distancia focal entre las distintas partes de la sección esférica se denomina aberración esférica. Si la superficie de una lente o espejo, en lugar de ser una parte de una esfera es una sección de un paraboloide de revolución, los rayos paralelos que inciden en cualquier zona de la superficie se concentran en un único punto, sin aberración esférica. Mediante combinaciones de lentes convexas y cóncavas puede corregirse la aberración esférica, pero este defecto no puede eliminarse con una única lente esférica para un objeto e imagen reales.

El fenómeno que consiste en un aumento lateral distinto para los puntos del objeto no situados en el eje óptico se denomina coma. Cuando hay coma, la luz procedente de un punto forma una familia de círculos situados dentro de un cono, y en un plano perpendicular al eje óptico la imagen adquiere forma de gota. Escogiendo adecuadamente las superficies puede eliminarse la coma para un determinado par de puntos objeto-imagen, pero no para todos los puntos. Los puntos del objeto y la imagen correspondientes entre sí (o conjugados) para los que no existe aberración esférica ni coma se denominan puntos aplanáticos, y una lente para la que existe dicho par de puntos se denomina lente aplanática.

El astigmatismo es un defecto por el que la luz procedente de un punto del objeto situado fuera del eje se esparce en la dirección del eje óptico. Si el objeto es una línea vertical, la sección transversal del haz refractado es una elipse; a medida que se aleja uno de la lente, la elipse se transforma primero en una línea horizontal, luego vuelve a expandirse y posteriormente pasa a ser una línea vertical. Si en un objeto plano, la superficie de mejor enfoque está curvada, se habla de ‘curvatura de imagen’. La ‘distorsión’ se debe a una variación del aumento con la distancia axial, y no a una falta de nitidez de la imagen.

Como el índice de refracción varía con la longitud de onda, la distancia focal de una lente también varía, y produce una ‘aberración cromática’ axial o longitudinal. Cada longitud de onda forma una imagen de tamaño ligeramente diferente; esto produce lo que se conoce por aberración cromática lateral. Mediante combinaciones (denominadas acromáticas) de lentes convergentes y divergentes fabricadas con vidrios de distinta dispersión es posible minimizar la aberración cromática. Los espejos están libres de este defecto. En general, en las lentes acromáticas se corrige la aberración cromática para dos o tres colores determinados.

(volver arriba)