La paradoja de Bell es un problema de relatividad que fue planteado originalmente en la cantina del CERN y que JohnBell describe detenidamente en el artículo "Cómo enseñar la relatividad especial" incluído en la colección "Lo decible y lo indecible en mecánica cuántica" (Alianza 1990). El planteamiento simple del problema es el siguiente:
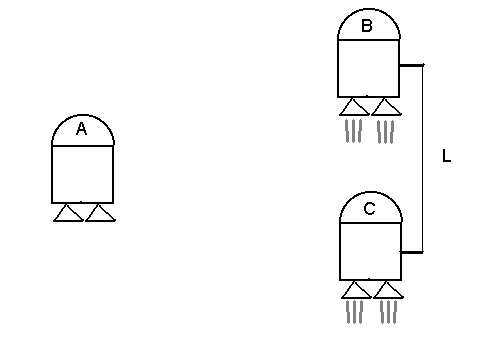
Tres pequeñas naves A, B, C se desplazan libremente por una región del espacio alejada de la influencia de cualquier otra materia, sin ningún tipo de rotación y sin ningún movimiento relativo, con B y C equidistantes de A

Tras la recepción de una señal de A, los motores de B y C aceleran suavemente. Supongamos que las naves son idénticas y tienen los mismos programas de aceleración. Entonces el observador en A advertirá que las naves B y C tendrán la misma velocidad en todo momento y que distancia entre ellas permanecerá constante. Supongamos que hay un hilo frágil atado a salientes de B y C que es justo lo suficientemente largo para cubrir la distancia L requerida. ¿Se romperá el hilo en algún momento?
La respuesta que da Bell es que sí, y la manera obvia de darse cuenta es pensar en que el hilo estará sometido a la contracción de Lorentz-Fitzgerald y no será con el tiempo (y por tanto el aumento de velocidad) capaz de cubrir la distancia necesaria. Pero la respuesta no deja claro quién ve la contracción, es decir, qué sistema inercial deberíamos tener en cuenta. La existencia de aceleración pone algo difícil la elección.
Desde mi punto de vista, uno puede aprender mucho intentando percatarse de lo que ocurre desde el punto de vista de los observadores B y C y resolver el ejercicio de una manera más costosa pero que zanjaría definitivamente la controvertida solución. Para ello tendrá que hacerse un tratamiento de un sistema acelerado dentro de la relatividad especial, sin acudir a las complejidades de la Relatividad General. ¿Cómo es esto posible?. Pues el secreto consiste en elegir sistemas de referencia (x',t') que en cada punto de la trayectoria de los cohetes se muevan instantáneamente con la velocidad del cohete, y por tanto donde éste estará en reposo instantáneo. Vamos a utilizar las propiedades de la trayectoria de los cohetes en el espacio de Minkowski (más conocidas como líneas de mundo) para ver de una manera intuitiva lo que ocurre. A modo de breve recordatorio solamente decir que en una representación de Minkowski, el sistema de referencia (x',t') que se mueve con velocidad v se representa como un sistema no ortogonal en el sistema de referencia inercial (x,t) donde se sitúa el observador que ve partir a los dos cohetes.
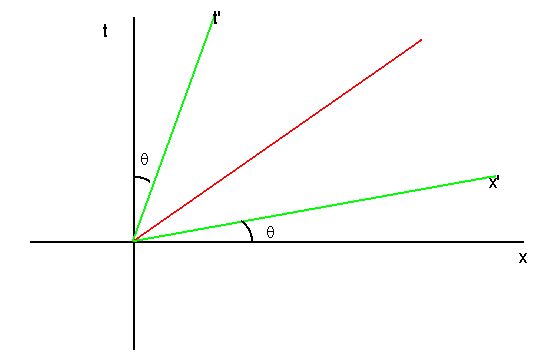
El ángulo q es tal que se cumple
Tan q = 1/v
Donde vamos a tomar la velocidad de la luz como la unidad, o lo que es equivalente, la coordenada vertical como c t.
¿Cómo representamos las líneas
de mundo de los cohetes acelerados?. Intuitivamente éstas deben
ser líneas curvas que parten del origen
verticalmente (inicialmente en reposo) y tiendan de forma asintótica
hacia una recta de pendiente 1, pues si se mantiene la
aceleración constante el cohete tenderá a alcanzar la velocidad
de la luz -Matemáticamente se puede comprobar que las líneas
de mundo de los cohetes corresponden a hipérbolas del tipo (x0
-x)2-t
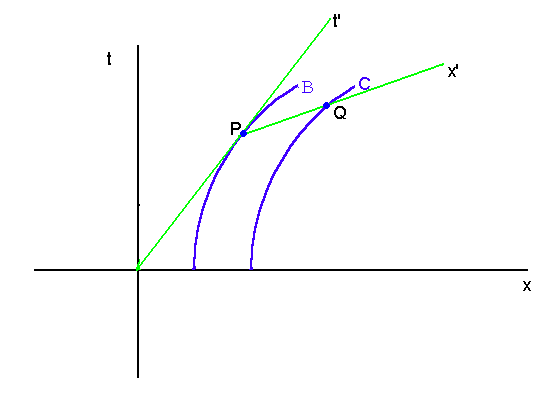
figura 1.
En la figura 1. se pueden ver estas líneas de mundo en azul. El el punto P, el sistema en el que el observador B se encuentra instantáneamente en reposo tiene el eje t' obviamente tangente a la trayectoria. Si trazamos entonces el eje de simultaneidad x' (según el observador B situado en P), el cohete C estará situado en el mismo instante en el punto Q. Puesto que el punto P ha sido elegido arbitrariamente, se podría realizar la misma construcción para puntos de la trayectoria situados en tiempos anteriores y en tiempos posteriores al punto P. Sólo hay que observar que el sistema (x',t') irá estrechándose sobre la asíntota de la curva a medida que la velocidad tiende a la velocidad de la luz y las distancias del tipo PQ medidas por el observador situado en el cohete B irán aumentando de manera indefinida con el tiempo: a la cuerda no le queda otro remedio que estirarse indefinidamente y romperse en algún lugar de la trayectoria.
Si nos fijamos ahora en la figura 3., se han trazado las líneas t' (x'=0) y t'(x'=g L). Es decir, las distancia propia de la cuerda que mediría un observador que se moviera con velocidad uniforme v igual a la que tendría el cohete B en el punto P, y que sería 1/(1-v2) veces la distancia L (distancia propia medida por el observador A).
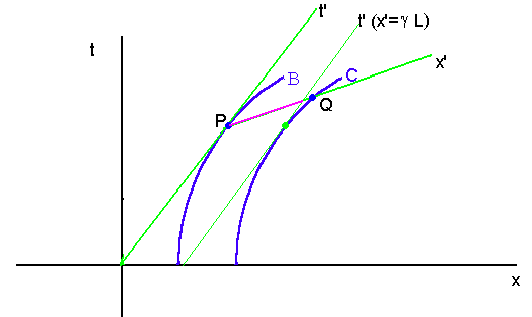
figura 3.
En la misma figura 3. también se puede apreciar el hecho de que la distancia PQ es ligeramente mayor que esta distancia g L (representada en color fucsia). Por decirlo de otra manera, el factor de contracción de Lorentz-Fitzgeral no explica en este caso concreto cómo relacionar las distancias medidas por el observador instantáneamente en reposo en B con las medidas por el observador situado en A. El efecto proviene obviamente de considerar la aceleración. Sin embargo, en una aproximación de primer orden cuando la distancia entre los cohetes B y C es pequeña en relación al factor g (cuando la velocidad se aproxima a la velocidad de la luz), esto es una buena aproximación.
Copyright 1996-2004 Pedro J. Hernández