H. E. Dudeney

Source

The following features of the order-6 magic star were reported by H. E. Dudeney in Modern Puzzles, 1926. This book has been included in it’s entirety in 536 Puzzles & Curious Problems Charles Scribner’s Sons, NY 1967 where this information appears in condensed form on pages 349-350.

Although Dudeney thought incorrectly that there were only 74 solutions, I have confirmed that these claims apply to all 80 solutions.

We must be full of admiration and amazement for this man who did so much for recreational mathematics, of which his work with magic squares and magic stars was but a small part. Also, let’s remember, he did it all without the help of computers, or even desk calculators.

Main Triangles

The cells a ,d, g & j, k, l at the points of the two main triangles will always sum to the same value. This value will be from 12 to 19 for one member of the complement pair, and from 27 to 20 for the other member of the pair with none adding to 14 and 25. The table below shows the number of solutions with each sum. Note how the totals correspond to those for the small triangle pairs (and for the total points sum).

Total of All Points	24 & 54	26 & 52	28 & 50	30 & 48	32 & 46	34 & 44	36 & 42	38 & 40
Each member, Comp.Pair	3 --- 3	6 --- 6	0 --- 0	2 --- 2	5 --- 5	7 --- 7	7 --- 7	10 ---10
Main Triangle Points	12 & 27	13 & 26	14 & 25	15 & 24	16 & 23	17 & 22	18 & 21	19 &20
Each member of Tri. Pair	6 --- 6	12 --- 12	0 --- 0	4 --- 4	10 ---10	14 --- 14	14 --- 14	20 ---20
Opposite small Triangles	9 --- 9	18 --- 18	0 --- 0	6 --- 6	15 --- 15	21 --- 21	21 --- 21	30 --- 30

Because the interior cells of each triangle is common to both triangles, the total for all the cells in each main triangle is
78 - triangle point total.

Because the total of the six points is always even, there can be no solution with consecutive numbers at the points.

If the sum of the three points of a large triangle is subtracted from 26, this difference, plus the value of one of the 3 points will be equal to the sum of the two valleys opposite. i.e. 26 - (J + K + L) = J + F + H.

Diamonds & Point Pairs

The three diamonds A + C + K + H, J + E + G + I and D + F + L + B each sum to 26.

One or two pairs of opposite points always equals 13. Three pairs of points never do.

Opposite small triangles

Opposite small triangles will always sum to the same value, i.e. A + B + I = E + F + K.
Due again to complement pairs, these totals also appear as pairs. The number of pairs of triangles that sum to each pair of totals are as shown in the bottom row of the above table.
Notice the correspondence to the large triangle point sums. The sums are exactly the same and the number of solutions for each sum is exactly 3 times as great. i.e. 6 small triangles and 2 large triangles per solution.

Class I, II, III

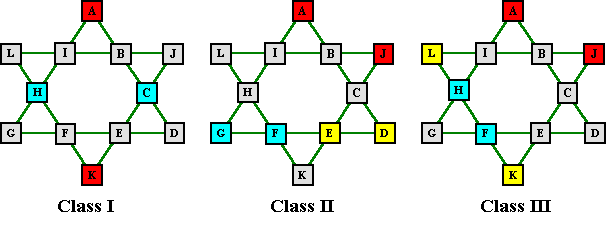
Another Dudeney claim was that all the solutions could be classified in three groups depending which of several pairs sum to 13. He referred to the first, and biggest, group as regular, and the other two groups as irregular. I simply call them class I, II and III.

This claim also checks out.
Both members of a complement pair belong to the same group.

The patterns below will often require rotation and/or reflection in order to match the basic solutions.

Total solutions of class I = 64, with 18 requiring 1 position of rotation and 28 requiring 2 positions.
With this class NO reflection is required because of horizontal symmetry.
Total solutions of class II = 8, with 6 requiring rotation and/or reflection to classify all solutions.
Total solutions of class III = 8, all of which required rotation and/or reflection.

Order6-3.gif (6213 bytes)

Please send me Feedback about my Web site!