 |
 |
 |
 |
 |
 |
![]()
![]()
Luo Shu Format magic Squares
Dr. Robert Dickter (DDS) announced in an email of Aug. 18, 2009 a series of magic squares with identical features to the order-3. He referred to them as Luo Shu format squares and shows a number of examples on his new website at www.luo-shu.com
Here I show the
Luo Shu and 3 examples followed by their common features. These magic squares
are easy to construct using a modified de la Loubére method.
The central themes of Luo Shu format squares is:
They contain a relationship between two consecutive numbers. In the case of the order-3, these are 1 and 2.
They will always contain a pythagorean triplet in a gnomon arrangement in the center of the square.
All are odd order, associated (center-symmetric) magic.
Some relationships between key numbers in all Luo Shu format magic squares.
|
a |
b |
order of square |
above x |
center cell (y) |
Lower right corner |
Constant |
Total of all #’s x2 * y |
|
1 |
2 |
3 |
4 |
5 |
6 |
15 |
45 |
|
2 |
3 |
5 |
12 |
13 |
15 |
65 |
325 |
|
3 |
4 |
7 |
24 |
25 |
28 |
175 |
1225 |
|
4 |
5 |
9 |
40 |
41 |
45 |
369 |
3321 |
|
5 |
6 |
11 |
60 |
61 |
66 |
671 |
7381 |
|
6 |
7 |
13 |
84 |
85 |
91 |
1105 |
14365 |
‘a’ and ‘b’ are two consecutive numbers whose sum equals the order of the square. 'a' always appears in the bottom row, 2nd cell from the right. 'b' always appears in the top right hand corner.
'y' is always the center cell. 'x' is adjacent to the left of 'y', and the 3rd member of the triad (y-1) is adjacent and above 'x'. The product of x and y equals the constant of the magic square, while x2 times y gives the total of all integers in the square. These 3 cells always form a pythagorean triad in a Luo Shu format square. They are indicated in red in the illustrations.
Beginning with order 9, the pythagorean triplet associated
with the next higher order also appears in the square in the position shown with
green numbers.
The number appearing in the lower right corner (purple) is the sum of the
numbers 1 to x (the order of the square).
|
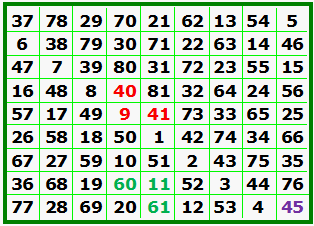
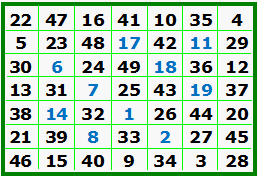
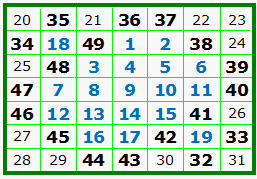
A. is the Luo Shu, the original and only order-3 magic
square (not counting rotations and reflections). B. is the algebraic representation of A. Compare x and y with the above table. C. is the order-5 Luo Shu format magic square. Compare colored integers with the above table. |
 |
 C. |
|
Here we see the order-7 and the order-9 Luo Shu format magic squares. On his web site, Dr. Dickter shows the Luo Shu type squares for orders 11 to 27. He explores the calendar, mysticism, and archaic religions in relation to the Luo Shu. |
|
 |
![]()
Topographical Magic Squares
In August, 2008, I posted an article about Craig Knecht’s Topographical magic
squares. [1]
Since then he and Walter Trump have expanded on this subject, and Craig has
posted a comprehensive page.
[2]
The basic premise is that the ‘height’ of each cell is based on the value of the integer in that cell. Then cells that are lower then the surrounding cells may contain ‘water’. Please refer to [1] or [2] for a complete description of topographical magic squares.
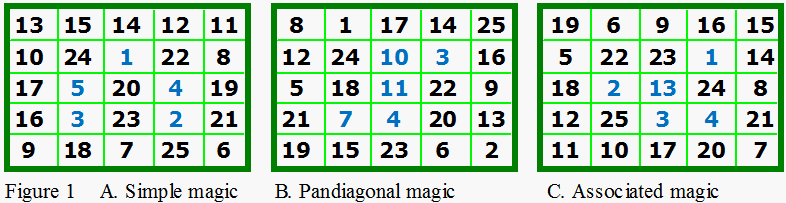
Shows 1 of 36 simple magic squares that hold the maximum of 69 units of water.
35 units retained is the maximum for order-5 pandiagonal magic squares. All 3600 order-5 pandiagonal magic squares contain water in only 5 different basic patterns. These range from 1800 different squares with 2 lake cells to 80 squares with the pattern shown in B. The units of water held range from 144 squares containing 8 units, to 352 squares containing 15 units. Squares exit that hold units of water from 8 to 30, and the 24 squares that hold 35 units.
59 units retained is maximum for an order-5 associated magic square. There are 48,544 associated m. s. 47,278 of these hold between 2 and 59 units of water. No pandiagonal associated order-5 magic squares hold water.
I suppose, to be consistent, we must say that figure 1(A) contains 2 ‘lakes’ of 2 cells each, and 1 ‘pond’ and (C) contains 1 lake and 1 pond. This follows from the fact that the basic definition states that no water can flow diagonally between cells.
|
The concept of topographical numerical squares may be extended. Following are several examples. A. Franklin’s "forgotten" order-8 magic square contains 3 ‘lakes’and 2 'ponds'. [3] B. An order-9 simple magic square with 1 lake, 2 ‘ponds’ and 3 ‘islands’. 780 units are retained. [4] |
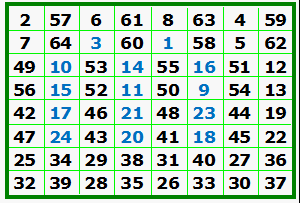 A. |
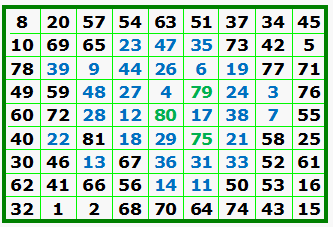 B. |
| C.The
Luo-shu type order-7 magic square contains 10 ‘ponds’ D. This order-7 magic square contains 321 units of water. [4] |
 C. |
 D. |
 E. |
Walter Trump has found an order-7 with 1 lake containing 365 units, and another order-7 with a lake and a pond that contains a total of 378 units. Are these the maximums for order-7 magic squares?
E. This is a number (not magic) square. (Disregard the fainter numbers. They are just inserted to complete the square.) The lake and the 2 ponds together retain 488 units of water. This is the maximum possible for an order-7 number square. [4]
[1]
Still More Magic Squares
[2]
http://www.knechtmagicsquare.paulscomputing.com/
[3] Paul C. Pasles, Benjamin
Franklin's Numbers, 2008, 978-0-691-12956-3, p.207
[4] These 3 squares were constructed by Walter Trump. He has a web site at
http://www.trump.de/magic-squares/
How many self-similar order-6
In an email dated August 12, 2009 Francis Gaspalou announced that he had successfully enumerated the number of order-6 self-similar magic squares (see example). He reported that there were 67,704,146,804,736 different squares of type a1+f1 = 37 (when counting all of the squares). There are the same number when a1+a6=37 so the total number of self-similar basic magic squares of order-6 is exactly 16,926,036,701,184 (ie 2 times 67,704,146,804,736/8).
 |
The same day, Walter Trump confirmed that total by reminding us that he had arrived at the same figure in October 2000. Walter had posted this figure (plus other magic Square enumerations) on the M. Suzuki site. [1] An Aside note: The Suzuki page refers to composite magic squares. What is actually meant is compact, a term defined by Gakuho Abe in 1950. [2] (Composite refers to magic squares composed of smaller magic squares i.e 9 order-4s make 1 order-12). |
Francis has a site where he shows results of various magic square enumerations and methods at http://www.gaspalou.fr/magic-squares/.
[1]
Most of Matsumi
Suzuki’s site is now at
http://mathforum.org/te/exchange/hosted/suzuki/MagicSquare.total.html
[2]
Gakuho
Abe, Fifty Problems of Magic Squares, Self published 1950. Later
republished in Discrete Math, 127, 1994, pp 3-13.
![]()
How many Bordered order 6
In an email March 29, 2009, Harry White sent a list of 140 borders to place around a non-normal order-4 magic square consisting of consecutive numbers. His web site [1] on this subject includes scripts to construct bordered squares of various orders.
|
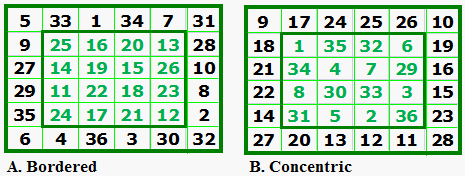
There is some
confusion over the difference between 'bordered' and 'concentric' magic
squares. |
 |
|
In the illustration, A is a bordered order-6 magic square. B. is a concentric magic square, but in this special case, the border consists of consecutive numbers. This is not required, and is in fact, quite rare! |
|
Totals for some
distinct orders of bordered magic squares are:
Order-5 = 2,880
Order-6 = 567,705,600
Order-7 = 6.14 x 1010
Harry`s page
[1]
contains totals
for all orders from 5 to 14.
For concentric order-6 magic squares Harry found the total was 736,347,893,760. This number was confirmed by Francis Gaspalou in July 2009.
[1] http://users.eastlink.ca/~sharrywhite/BorderedMagicSquares.html
![]()
Totally Irregular Magic Squares
On August 24,
2009, Francis Gaspalou introduced a new type of magic square which he calls
totally irregular.
A lively email discussion followed, between him, Aale de Winkel and Walter
Trump.
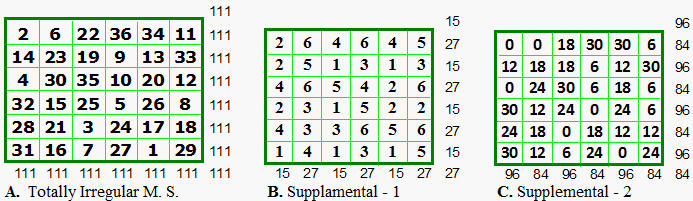
A. (above) is
the totally irregular simple magic square received from Francis Gaspalou. Aug.
24, 2009
More on this subject may be found on his web site.
[1]
Magic squares may be constructed by using two subsidiary squares which are then added on a cell by cell basis to form the final square. Such squares may then be divided into 2 broad classifications.
A Regular magic square [2] is one where each number (in the classical version, each letter) appears once in each row, column, and diagonal. If such a square could exist for order-6, then each line would total 21 in subsidiary square A and 90 in subsidiary square B. Prof. Candy reported that there are 38,102,400 regular magic squares of order-7. [3]
An Irregular magic square is one where this is not the case and a number may appear more then once (or not at all) in at least 1 row, column, or diagonal. For example, there are no irregular pandiagonal magic squares of order less the 7, but both Trump and Gaspalou found that there are many more then the 640,120,320 different ones of that order reported by Prof. Candy. [4]
A Totally Irregular magic square (as the one shown above) is one where all the lines are irregular in both subsidiary squares. The total number of these (for any order) is still unknown.
[1] Francis
Gaspalou’s web site is http://www.gaspalou.fr/magic-squares/.
[2] W. H.
Bebson and O. Jacoby, New Recreations With Magic Squares, Dover Publ.,
1976, 0-486-23236-0
[3] Professor A. L. Candy of
University of Nebraska (1890s to 1945) did much original research on this
subject. A self-published book and some of his notes are in the
Strens Recreational Mathematics Collection at the University of Calgary.
[4] In an email dated Oct.4, 2009, Francis showed totals for several small
sub-sets of order-7 pandiagonal magic squares. These were sufficient to indicate that
Candy's total for irregular pandiagonal magic squares is far too low.
Postage Stamps and Magic Squares
After retiring from the
Department of Mathematics and Statistics, McGill University, in 2005, Professor
Emeritus George Styan [1] became interested again in magic squares.
In 2007 with Götz Trenkler, George prepared a bibliography [6] of over 300
references on magic squares. George soon combined this interest in magic squares
with his lifetime fascination with stamp collecting. In August 2009, he sent me
copies of a recently accepted paper and the pdf-file for the overheads of a talk
he gave on the study of magic squares as related to stamp collecting.
[2][3][4].
From the abstract of Some Comments On Philatelic Latin Squares From Pakistan [2]
We explore the use of Latin squares in printing postage stamps,
with special emphasis
on stamps from Pakistan. We note that Pakistan may be the only country to have
issued
postage stamps in 2x2; 3x3; 4x4 and 5x5 Latin square formats: we call such sets
of
stamps philatelic Latin squares (PLS)….
Here are three illustrations from that paper.
The sheetlets displayed in
Figures 1.1 and 1.3 are examples of 2x2 philatelic Latin squares (PLS). The
stamps in the left panel (fig. 1.1) depict Mustafa Kemal Atatürk (1881--1938),
founder of the Republic of Turkey as well as its first President, and
Quaid-e-Azam Muhammad Ali Jinnah (1876--1948), who is generally regarded as the
founder of Pakistan.
The stamps on the right (fig. 1.3) feature Alexander Sergeyevich Pushkin (1799–1837), who
is considered to be the greatest Russian poet.
The authors do not discuss
magic squares per se, but consider various aspects of Latin Squares and their
newly defined PLS. They also discuss Gerechte Latin squares and the somewhat
related Sudoku square in some depth.
Here is another illustration and some of the accompanying text.
|
Featured in the 5x5 PLS
here are five antique automobiles from the late 19th and (very) early 20th
century (from left to right in the first row): Following are three of the four stamps that George Styan found that actually depict a magic square. These are taken from An Illustrated Philatelic Introduction to Magic Squares. [3] See also [5] |
|
|
The Franklin USA stamp consists of a collage of 4 items from Franklin history. Here also is an enlarged view of the order-8 bent-diagonal square. This is only semi-magic because the two diagonals do not sum to the constant. George thinks there are at least 160 stamps associated with Benjamin Franklin, but only one that shows a magic square.
|
|
|
|
MELENCOLIA:I by
MELENCOLIA:I by
Not shown is George says there are over 200 stamps associated with Albrecht Dürer and wonders if, maybe, there are more stamps for Franklin than for Dürer? |
|
|
[1] George P. H. Styan may be reached at styanatmath.mcgill.ca
(note the 'at').
[2]
Ka Lok Chu, Simo Puntanen, and George P. H. Styan: Some comments on philatelic
Latin squares from Pakistan. Invited paper to appear in the
Special Silver Jubilee issue of the Pakistan Journal of Statistics: preprint 43
pages.
[3] An Illustrated Philatelic Introduction to Magic Squares (in honour of Dr.
Peter Loly’s retirement). Invited talk presented at The University of Manitoba,
Winnipeg, on 9 November 2007. Overheads (pdf file): 52 heavily illustrated
pages.
[4] Peter D. Loly and George P. H. Styan: An introduction to philatelic Latin
squares, with some comments on Sudoku. Report 2009-01 from the
Department of Mathematics and Statistics, McGill University, Montréal. In
preparation.
[5] Oskar Maria Baksalary, Ka Lok Chu, George P. H. Styan and Götz Trenkler: A
philatelic introduction to magic squares associated with
Albrecht Dürer (1471--1528), Benjamin Franklin (1706--1790) and Johannes Hermann
Zukertort (1842--1888). Report 2009-04 from the Department of Mathematics and
Statistics, McGill University, Montréal. In preparation.
[6] George P. H. Styan and Götz Trenkler: An annotated bibliography on magic
squares, with special emphasis on linear-algebraic results, as well as on very
old and very new results. Report 2007-02 from the Department of Mathematics and
Statistics, McGill University, Montréal. Includes 318 references.
![]()
1040 Order-4 Magic Squares
On September 6,
2009 I received an email from Lee Sallows with two documents attached
[1][2].
(Actually, most of this work on this subject was done about 10 years ago.)
Folowing are the first two paragraphs of NEW ADVANCES WITH 4 X 4 MAGIC SQUARES by Lee Sallows
Introduction
One of the best known results in the magic square canon is Bernard Frénicle de Bessy's enumeration of the 880 ‘normal’ 4´4 squares that can be formed using the arithmetic progression 1,2,..,16. A natural question this suggests concerns non-normal squares: Is 880 the largest total attainable if any 16 distinct numbers are allowed?
The answer is no. A computer program that will generate every square constructable from any given set of integers has identified 1040 distinct squares using the almost arithmetic progression: 1, 2, 3, 4, 5, 6, 7, 8,10,11,12,13,14,15,16,17. Note the doubled step from 8 to 10. Extensive trials with alternative sets make it virtually certain that 1040 is the maximum attainable (or 8 ´ 1040 = 8320, if rotations and reflections are included), although an analytic proof of this assumption is lacking. A listing of the 1040 squares can be had on request via email at lee.sal@inter.nl.net.
In this paper he goes on to examine the FERTILITY of alternative sets of 16 numbers, meaning the number of magic squares yielded by each. Tables listing the fertilities of both symmetric and asymmetric sets are given.
Here are 3
example order-4 squares taken from his index ordered list of 1040 magic squares
using the above number set (figures A, B, C).[3]
The two numbers above each square are the index number and the Dudeney Group
number.

The quantity of squares in each of the 12 (traditional) Dudeney groups for this number set is
|
Dudeney Group |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
# of Squares |
48 |
48 |
48 |
96 |
96 |
480 |
52 |
52 |
52 |
52 |
8 |
8 |
The second document I received was A SET USING 1, 2, 3, 4, 6, 7, 8, 9, 10 11, 12, 13, 15, 16, 17, 18.
The second document received was a NON-ARITHMETIC progression of 16 integers that yield 880 4x4 magic squares.[2]
This list of 880 squares (using 8 complementary integer pairs) includes 6 with distributions that are DIFFERENT to the usual 12 Dudeney types, such as the examples D and E above.
If you wish, you may review the 12 original Dudeney groups here.
A subsequent paper [4] received on 9/9/09 from Lee Sallows identifies a total of 22 additional Dudeney type diagrams and a representative magic square for each. Unlike the original Dudeney types, these apply only to magic squares that consist of non-consecutive numbers. Of course, from Lee Sallows and most other mathematicians perspective, the normal magic squares are only a sub-set of all number magic squares!
[1]
New Advances With 4 X
4 Magic Squares
by Lee Sallows New_Advances_(4).doc
[2] A set using 1, 2, 3, 4, 6, 7, 8, 9, 10 11, 12, 13, 15, 16, 17, 18 by
Lee Sallows 880 New Squares.doc
[3] MS1040.txt received Sept. 3/09 lists all 1040 squares in index order.
[4] On non-normal Graphics Types by Lee Sallows (On non-normal graphics
types_1-2.pdf)
That Amazing 1089
The Luo Shu multiplied by 1089 gives us a magic square with the magic sum of 16385.
 |
The 3 Most
Significant Digits of the numbers in this square gives us another magic
square with a sum of 1632. The 2 MSD give us another magic square as do the 3 and the 2 Least Significent Digits. |
Finally, the 1 MSD give us a 180 degree rotation of the original magic square for a total of 7 different magic squares!
![]()
Palindromic Magic Squares
Eight additional squares derived from square A. How many more variations can you find? [1]
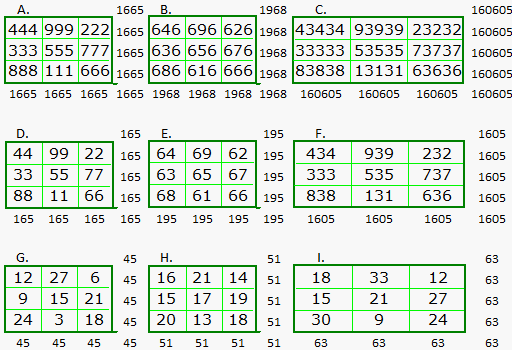 |
A. Original Luo Shu but with 3 digit redigits. B. 1 digit of A. with arbitrary first and last digits C. The 3 digits of A. with arbitrary 2nd and 4th digits inserted.
D. First and second digits of A.
Sum of the digits in each cell of A. |
[1] Adapted from Emanuel Emanouilidis: Journal of Recreational Mathematics:29:3:1988:177-178
W. S. Andrews error
On August 18,
2009, Peter Loly reported (by email) a minor error in W. S. Andrews Magic
Squares and Cubes.
In figure 253 (page 143) the cell in the bottom row, sixth column is incorrect.
It should be a+2d+2c+b.
This correction provides the correct integer for the corresponding cell in the
order-9 numerical magic square shown
in figure 254. In Andrews first addition, figure 253 (actually fig. 270 there)
is correct.
![]()
Magic Square Pair
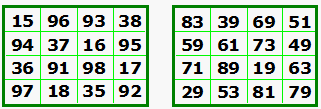 |
Digits in second table are the reverse of the first one. In each case, if the 2nd digit of each number is removed, the square is still magic |
[1] Dr. Crypton, Timid Virgins Make Dull Company, Penguin Books, 1985, p 149, 01400-80430
Shineman – 4 Related
I received these
4 related magic squares from Ed Shineman Jr. of New York on January 9, 2001
I have since lost contact with him after he passed his 90th birthday.
Ed was not much on the theory of magic squares, but had a creative imagination.
I have taken this item from a 2 inch stack of material received from him over
the years, and include it as a tribute to him.
|
Together, the first 3 magic squares use the consecutive numbers from 1 to 97. The two order-4 squares each use the numbers 10, 11, 21, 22, 32, 33, 43, 44, 54, 55, 65, 66, 76, 77, 87, and 88. The order-9 composite square uses the remaining numbers. |
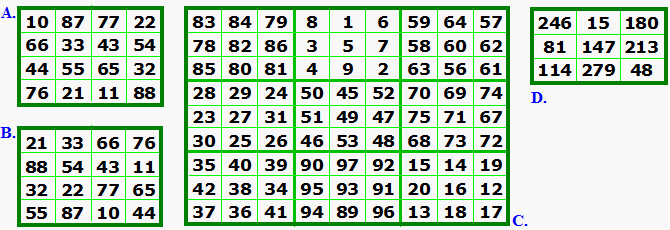 |
The magic constant of the 9 order-3 squares form another order-3 square.
Is Associated semi-pandiagonal
Is Pandiagonal magic
Is a simple composite magic square
Is associated magic (as are all order-3 hypercubes)
Other Shineman creations on my site are on my Unusual Magic Squares and my Material from REC pages.
Please send me Feedback about my Web
site!![]()
![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
This page originally posted October 2009
This page last updated
October 07, 2009
Copyright © 2009 by Harvey D. Heinz