3.2 Hyperbolic Current Threads
| |
|
The nature shows us only the tail of a lion. But I have no doubts that the lion really exists, though it cannot appear as a whole at once due to its large size.
|
Albert Einstein
|
The most symmetrical (after inertial) motion – uniformly accelerated – is selected for the threads of current of an electron, when the acceleration is constant in its intrinsic (instantly accompanying) inertial system of reference:
| (1 – v2)da + 3(va)adt = 0, adt := dv. |
(13) |
Metrics with signature (+ – – –) is assumed. The equation for uniformly accelerated motion is written in four- and three-dimensional values defined in a standard manner:
| ui := |
|
= l |
|
= (l; lv), l := |
|
= |
|
, |
|
(2.l) |
| uiui = (l; lv)(l; –lv) = l2(1 – v2) = 1, |
(2.l2) |
| widt = (ldl; lvdl + l2dv), dl = l3vadt. |
(2.dl) |
Uniformly accelerated motion conserves the square of 4-acceleration along the universe line:
| wi(s)wi(s) = –l6(aa – [va]2) = –w2(s0), |
(3) |
that enables to write the equation (14) in more simple four-dimensional form:
|
|
– w02ui = D2ui – w02ui = 0, D := |
|
. |
|
(4) |
The symmetry described is assumed to be global, i.e. w0 is a common constant not only along the line of current, but also for all threads of current of two signs of charge. w0 is made equal to one by selecting the system of units:
Natural values of length L=c2w0–1 and time T=cw0–1 appear as values derived from fundamental constants – the speed of light and acceleration in an intrinsic system of reference.
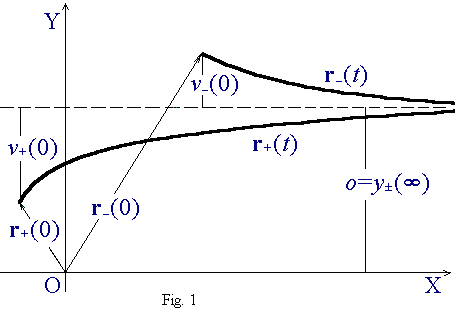
Symmetries of current threads of an electron afford motion in OXY plane passing through the center of symmetry. One solution branch is selected, starting at zero moment of time in the vertex (return point) where vertex 3-radius-vector r0 and vertex 3-velocity v0 are orthogonal, and going into spatial infinity, at large t, parallel to OX axis in positive direction:
| r(t) = (x, y) = (t m k + ε(t), o(k m ε(t))), |
(7.r) |
| v(t) = (vx, vy) = (1 – |
|
, ± o |
|
), |
|
(7.v) |
| o = v0l0, kl0 = r0 ± 1, ε(t) l02 = l – t. |
(7.d) |
The whole set of solutions is a natural combination of two qualitatively different families corresponding to the paths of ONs with different sings of charge. It is the major marvel of uniformly accelerated motion. It is worth spending time and efforts to get acquainted with it!
Lines of current of positive charge correspond to set of solutions obtained by selecting upper sign in symbols «±» and «m», and lines of current of negative charge by selecting lower sign. The solution includes two undefined functions of vertex velocities.
Let's construct one branch of line of current for positive and one for negative charge with the same impact parameter
| o = v0+(r0+ + 1) = v0–(r0– – 1), |
(8) |
when time varies from zero to plus infinity during motion from the vertex into spatial infinity with common asymptote parallel to OX.
| r0 = r0(m |
|
, v0), v0 = v0(v0, ± |
|
). |
|
(9) |
Lines of current of the positive charge thicken near the center (are attracted to it), and lines of current of the negative charge rarefy (are repelled from the center). This is the case when the motion is pure tangential at the vertex of the path (return point). If there is a radial motion component, as it is in general case, there is an additional repulsion force from the center (along velocity vector) independent of charge sign. This «antigravity» component, which is responsible for decrease of velocity when approaching center and its further increase when going from the center is the result of variation of ONs at rest mass depending of field value, but not the result of action of another force field! But let's proceed in succession…
Let's formally define the vectors p and F:
| p := mlv, dp := Fdt, |
(10) |
constructed basing on undefined function m(t,r0) and known values of uniformly accelerated motion (7). From this, we shall obtain two equations by differentiating and making elementary transformations:
In (11), 3-vector of acceleration a is developed in 3-vector of velocity v and 3-vector obtained by differentiating 3-vector p defined by equation (10) in respect to time. Only values contained in (10) are used. Equation (11) is assured by definition (10) independently of specific form of 3-vector of velocity, i.e. (11) is the sameness. In (12), 3-vector of acceleration is obtained from 3-vector of velocity (7.v) by differentiating in respect to time, and is developed in 3-vector of velocity and 3-radius-vector (7.r). This development reflects the structure of hyperbolic motion (7). If the following equations are true
(11) and (12) are the same, that is possible when
In this case, the moment of the vector along the line of current is conserved automatically:
The constant of integration in (14) related to an ON and proportional to its charge δq is made equal to the absolute value of the charge being carried by fixing the relation between mass and charge units:
Then the ON is related to the values
contained in the «law of motion»:
There are formally discriminated vertex velocities for which
and when the whole equation is significantly simplified:
| l = r ± 1, δm = |
|
, E = – |
|
|
|
. |
|
(20) |
But what is the physical meaning of these constructions?
1) If we define the mass and the impulse of the ON in accordance with (17), the uniformly accelerated motion is the consequence of the «law of motion» (11), (18) in the field described by the same system of equations.
2) Mass and impulse may be defined using the law of conservation of the moment of impulse (as an integral of equations of motion not formulated clearly) when an ON moves along the line of current, and obtain (17) again.
3) «Equations of motion» look as natural generalization of relativistic equations of motion with invariant mass in case of motion with variable mass-function of field G. The first summand in (11) formally is the same as common relativistic law of motion if the filed of electron is fixed in accordance with (18.E). The second summand in (11) takes into account the variation of mass which may be formally interpreted as the additional «antigravity» field. This possibility has been used in the scalar theory of gravitation of Gunnar Nordström (1912) to define gravity field in case of conservation of the velocity of light.
4) Uniformly accelerated motion defines the field of electron (18) having necessary Coulomb asymptotics by all the above methods.
5) Field character of the mass is evident. It is exactly according to Ernst Mach (Albert Einstein) the mass of an ON is determined by the motion of all ONs in the whole space through the field generated by them in the vicinity of the point. In any case, this was the way Einstein has understood it and he has given this idea the name his predecessor – the MACH PRINCIPLE.
6) The isotropy of ON velocities at the infinity restricts the form of admissible vertex velocities for large r0 by such that the ratio to k is asymptotically unit. This results in a unit electron charge, i.e. the factor with the dimension of a charge contained in asymptotically Coulomb electron field (18.E). Now we speak about active field of electron which, along with law of motion (18), generates the set of lines of current of two charge signs in the whole space. In turn, lines of current, in accordance with ML-equations, generate their own integral field – passive field of electron. These two fields must be identically equal. The field of electron, in accordance with the equations of motion, forms current threads of sources which, in accordance with ML-equations, generate the field of electron…
7) In the special theory of relativity, the square of 4-vector is a 4-scalar, i.e. it is invariant in respect to rotation of four-dimensional reference system including common spatial rotations and Lorentz transformations. But this invariance is local, it is restricted by the case when 4-rotations are made in a fixed world point and corresponding 4-scalar is a function of this world point.
The square of 4-velocity (for an arbitrary motion) the 4-scalar of which is equal to unit globally is an exceptional case. In the same way, 3-velocity of light in an arbitrary inertial reference system is globally a unit. Both square of 4-velocity of some arbitrary motion and square of 3-velocity of light in any inertial system of reference are equal (to unit) as the result of their construction. In case of uniformly accelerated motion, both the square of 4-acceleration and the square of 3-acceleration in an intrinsic system of reference are also GLOBALLY INVARIANT (equal to one up to a sign) by definition. The condition of conservation of 4-radius-vector along the line of current
| xixi = t2 – r2 = –r02 |
(21) |
is almost the same as the equation of the line of current in the system of an electron at rest K0:
To achieve «complete identity», one should use the group of conformal transformations by redefining linear element. All necessary material may be found in Nordström theory where the relation between field mass at rest, «antigravity» field (in case of sign reversing) and conformal factor in linear element is clearly visible. At the same time, the mysterious uselessness of conformal group conserving ML-equations along with Lorentz group is eliminated. All the above enables us to give rise to the question of enhancing the special principle of relativity to the HYPERBOLIC PRINCIPLE.