ортогональной вектору E(r) и отложенный из точки P в направлении вектора g(θ); вектор магнитного поля B и единичный вектор b направлены перпендикулярно плоскости рисунка из P.
Ричард Фейнман |
Привожу полный адрес этого «признания» Ричарда Фейнмана:
Фейнмановские Лекции по Физике – ФЛФ
6 Электродинамика [28]
Глава 27 Энергия Поля и его Импульс
§4. Неопределённость энергии поля [с.293-294],
чтобы использовать особые преимущества обсуждения проблемы на прекрасно оборудованных под неё базовых «территориях» этой и следующей за ней
Глава 28 Электромагнитная масса
главы ФЛФ. Там содержится коллекция великолепных фейнмановских эскизов со знаменитых «дыр» электромагнетизма, равно как и мастерски выполненные наброски с предлагавшихся разными авторами проектов их устранения или включения в Теорию. Ричард Фейнман был крупнейшим специалистом в области анализа и классификации всех этих возможных и невозможных способов разрешения труднейших проблем электромагнетизма, мучивших физиков ещё со времён Фарадея и Максвелла. Он сам, пусть и не без помощи Джона Уилера, в период своего профессионального развития методично переболел всеми этими вариантами надежд, раз за разом убеждаясь в необходимости поиска другого, доселе неиспытанного пути. Фейнман был одним из немногих благополучных физиков квантовой эпохи, потратившим исключительно много времени и сил на длительные и изнуряющие экспедиции к этим всё ещё непокорённым вершинам классической эпохи. Он сам, будто бы изначально, твёрдо знал и неоднократно делал попытки убедить в этом других, включая и многочисленных читателей ФЛФ, что глубинные, исконные причины, повлекшие неизбежные «блеск и нищету» КЭД, непосредственно связанны с самими идеями теории Максвелла и которые не имеют непосредственного отношения к квантовой механике. [28,гл.28,с.305]
Эти главы ФЛФ конечно же содержат описание и определение и необходимых нам здесь понятий, и общепринятой символики, и прочего инструментария, включая даже приготовленные, будто бы для нас, формулы и поясняющие рисунки. Предварительная (или параллельная) проработка материала этих глав поможет читателю лучше подготовиться к активному прочтению этой статьи и, возможно даже, поможет найти свою, ещё никем неизведанную потайную тропинку… Здоровая доля самоиронии, царящая в ФЛФ, – в этом идеально приспособленном для физических прогулок к яблоне месте, – способна деликатно настроить читателя на нужную тональность и снабдить его уникальными подсказками и настроем для успешного овладения заветными истинами. А они, пребывая до поры где-то в недрах всей этой неизбежной пока что кучи слов, при всей своей кажущейся недоступности, терпеливо дожидаются своего покорения настойчивыми и пытливыми исследователями.
Трудность, о которой я собираюсь говорить, связана с приложением понятий электромагнитного импульса и энергии к электрону или другой заряженной частице. [28,гл.28,§1,с.306]
В соответствии с теоремой Пойтинга и ФЛФ (формулы 27.14 и 27.15):
| 2u = EE + BB, S = [EB], | (1) |
где: u – плотность энергии поля, т.е. количество энергии в единице объёма пространства; S – поток энергии поля, т.е. количество энергии, прошедшее в единицу времени через единичную поверхность, перпендикулярную к потоку; E – вектор электрического поля; B – вектор магнитного поля. Выражения для u и S здесь выглядят проще в сравнении с ФЛФ благодаря использованию естественной системы единиц измерения, в которой
| ε0 = μ0 = c = 1. | (2) |
Аналогично тому, как это делается в гл. 28, §2 – Импульс движущегося заряда, займёмся пространственным распределением плотности импульса электромагнитного поля движущегося положительного заряда q. Будем считать, что скорость равномерного движения v заряда q много меньше единицы и сохраним в разложении по степеням v только величины до первого порядка малости включительно. В этом приближении электрическое поле E(r) сохраняет сферическую симметрию статического случая и появляется магнитное поле B(r,θ) в качестве единственной релятивистской поправки первого порядка. Плотности электромагнитных энергии u и импульса g на расстоянии r от заряда q принимают значения:
| 2u = E2(r), g = [E(r)B(r,θ)] = gt, | (3) |
| g = E(r)B(r,θ) = 2·uv·sinθ, | (4) |
| B(r,θ) = [vE(r)] = B(r,θ)b, B(r,θ) = vE(r)sinθ, | (5) |
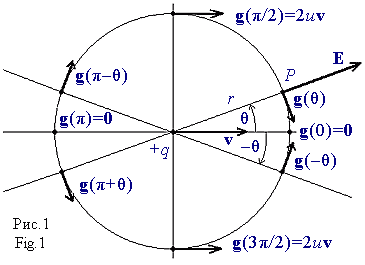
где: θ – угол между направлением скорости движения v заряда q и вектором электрического поля E(r) в точке P; t – единичный вектор, ортогональной вектору E(r) и отложенный из точки P в направлении вектора g(θ); вектор магнитного поля B и единичный вектор b направлены перпендикулярно плоскости рисунка из P.
Необходимо особо отметить, что множитель sinθ появился в скалярной величине g(θ) вектора плотности импульса g(θ) в качестве сомножителя, входящего в скалярную величину B(r,θ)=vE(r)sinθ вектора магнитного поля B, равную произведению скалярных величин векторов v и E(r) на синус угла между ними. Операция проецирования g(θ) на направление вектора скорости v ещё не производилась! Полученная пропорциональность величины g синусу угла θ приводит к очень странной «циркуляции» вектора плотности импульса g(θ) вдоль меридианов сферических поверхностей радиуса r от заднего полюса при θ=π к переднему с θ=0, лежащим по разные стороны от заряда на оси его движения. Пара таких меридианов, лежащих в плоскости нашего рисунка, отобразились на нём как верхняя и нижняя половинки окружности, рассечённой горизонтальной осью движения и симметрии.
В этом заключается основная часть трудности. Другая её часть заключена в множителе 2, который появился в результате замены E2(r) на 2u на последнем этапе получения выражения для g в формуле (4). На экваторе сферической поверхности, который отображён на рисунке верхней точкой при θ=π/2 и нижней при θ=3π/2, получена плотность импульса 2·uv, что ровно в 2 раза превышает «желанное» uv для всего пространства, независимо от угла θ. Эти трудности теории поля, связанные с появлением катастрофических множителей sinθ и 2 в выражении для полевых величин плотности импульса g=uv·2·sinθ, «помноженные» на крайне неприятную меридианную циркуляцию плотности импульса g во всём пространстве, порождены применением выражений Пойтинга для плотностей энергии и импульса электромагнитного поля!
Вдоль всей оси движения заряда локальная плотность импульсов g(0) и g(π) нулевая. В конической окрестности этой оси в силу присутствия множителя sinθ величина g исчезающе мала, несмотря на конечную величину плотности энергии поля u, совершенно не зависящую от угла θ. При проецировании вектора плотности импульса g на направление движения заряда появится в качестве множителя ещё один sinθ, после чего величина вклада полевого импульса из нашей конической окрестности в интегральный полевой импульс движущегося заряда станет пропорциональна sin2θ, т.е. ещё незначительней. Непропорционально большой вклад в полный электромагнитный импульс заряда приходится на экваториальную область поля движущегося заряда, тогда как вклад из полярных областей поля обеднён пропорционально sin2θ. Это обстоятельство и послужило решающим основанием при выборе заголовка статьи – Коническая Дыра в Импульсе Электрона.
| Последние изменения: 28 января 2003 | EN | Вернуться к оглавлению |
| 28. | Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике: Пер. с англ., вып. 6. кн. 4 – М.: «Мир», 1977 |
|
Основная страница – http://www.ltn.lv/~elefzaze/ html/php вёрстка: Александр А. Зазерский ©1998–2004 Александр С. Зазерский |
|
|