La Tercera Dimension

Esto parece un titulo sacado de Star Trek :-) Pero noooo, ni mucho menos, jejeje. Es que no sabia como llamar a este nuevo tutorial, asi que le he puesto este nombre que le va como anillo al dedo. En este tutorial vamos a profundizar un poco mas en algunos aspectos que hemos visto en los tutoriales anteriores, para tener todo mucho mas claro. Ademas veremos algunas cosillas nuevas y haremos otro pequeño programa. :-)

En este tutorial no hay codigo fuente, la mayoria de codigo que aparece pertenece a un proximo tutorial donde si que habra un pequeño programa, y por supuesto tambien podras bajarte el codigo fuente.

La Tuberia de Direct3D

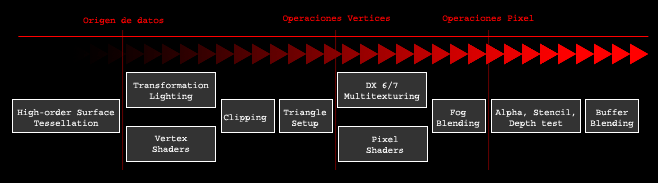
Esta es la traduccion literal de "Direct3D pipeline" y viene a significar mas o menos como funciona Direct3D si lo comparamos con una tuberia (o una cadena de produccion de cualquier fabrica). Las cosas entran por un lado, se realizan una serie de operaciones, y tachannn por el otro lado salen las cosas ya hechas. Lo importante de esta cadena es entender en que orden se efectuan esta operaciones:

Aunque algunos nombres esten en ingles, creo que mas o menos se entiende facil. Este es el modelo actual de Direct3D en la version 8. Una de las novedades respecto a modelos anteriores es el Vertex Shader. Algunos programadores prefieren implementar ellos mismos sus propios algoritmos de transformacion y efectos de luz, es decir, que se pueden desactivar algunas partes de esta "tuberia" y enviar la informacion a sus propias rutinas. Pero normalmente nada de esto es necesario porque Direct3D es realmente rapido, especialmente con las nuevas tarjetas ATI Radeon, NVIDIA GeForce2 Ultra, S3 Savage 2000, etc...

Gracias a estos nuevos procesadores, las operaciones de transformacion y de luz (de ahora en adelante T&L, de "Transformation and Lighting") se realizan en la propia tarjeta grafica, en vez de en la CPU. Asi que una vez liberada la CPU de la carga de realizar las operaciones de T&L, podemos usarla para otros fines en los juegos tales como Inteligencia Artificial y complejos calculos fisicos.

La Tuberia de transformacion

Una de las partes importantes de esta "tuberia" es la que se dedica a la Transformacion. Pero que es la Transformacion??? llevo hablando de ella unos parrafos y todavia no sabemos lo que es:

Basicamente consiste en las operaciones que realizamos para transformar los valores de nuestro mundo 3D entre los diferentes espacios que lo componen. Es decir, descomponemos nuestro mundo 3D de acuerdo a diferentes momentos o diferentes sistemas de coordenadas mas sencillos para trabajar con el, ya que si no seria demasiado complicado trabajar sobre el. Estos diferentes sistemas se llaman "espacios".

No se porque todo en este tutorial me esta recordando a Star Trek :) tanto espacio y tanta tuberia y tanta dimension... jejeje.

Bueno, vamos a ver cuales son estos espacios: espacio-modelo, espacio-mundo, espacio-vista y espacio-proyeccion.

Esta tuberia transforma cada vertice de un objeto, desde un punto abstracto en el sistema de coordenadas, a un pixel de la pantalla. Teniendo en cuenta las propiedades de la camara virtual desde la que se ve la escena. Para realizar estas transformaciones necesitamos 3 matrices que definan nuestros "espacios". La Matriz-Mundo, la Matriz-Vista y la Matriz-Proyeccion.

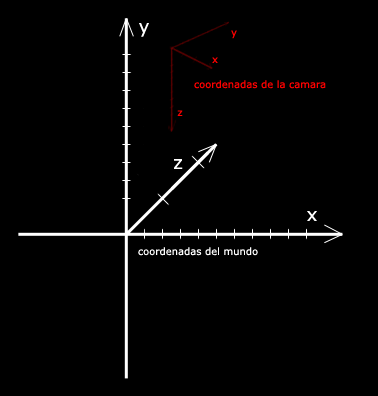El seguno de los pasos, "Transformar Vista" transforma los objetos desde el espacio-mundo al espacio-vista (o camara). En este punto podemos decir que tenemos ya una vista 2D mas o menos aproximada de lo que la camara ve de nuestro mundo en 3D. En esta parte tambien se aplican calculos de luz de "backface culling" (es decir, que caras se muestran y cuales estan ocultas).

Por ultimo tenemos "Transformar Proyeccion", que segun sean los campos de vista horizontal y vertical de nuestra camara crea una adaptacion de nuestro modelo-mundo que podamos representar en el monitor "pixel-a-pixel".

Los objetos que estan mas cerca a la parte frontal del "frustum" se expanden, y los que estan mas lejos se encogen. La adaptacion se hace a partir de la geometria del frustum de la camara a una forma de 4x4. Esto se es posible a traves de una matriz de proyeccion construida a partir de del campo de vision (FOV, Field of View) o tambien llamado "Viewing Frustum", un aspect ratio, un plano de corte frontal (o Frontal Clipping), y un plano de corte trasero (o Back Clipping)

Vamos, que esta explicado en el dibujo de un poco mas arriba. Si no lo has entendido todo no te preocupes, puedes asemejar este ultimo proceso como elegir la lente apropiada a nuestra camara... segun la lente que pongamos veremos el espacio-mundo de una forma u otra.

Un poco de matematicas

>Joer tio, no me digas que ahora vamos a empezar a ver ecuaciones y rollos de logaritmos y cosas de esas???

noooo, no te preocupes!!! Yo tambien odio las matematicas, asi que no me voy a poner a explicar nada de matematicas que no sea lo basico para entender lo que vamos a trabajar a hacer en los proximos programas. Las matematicas que vamos a usar son muuuy sencillas y cualquier niño del cole las entenderia. No hace falta que vayas a desempolvar los libros de COU !! :) Aunque te recomiendo que cogas un boli y de pongas a probar lo que ves en el tutorial sobre el papel a ver si lo has pillado o no (si no lo estas haciendo ya)

Imaginemos el tipico F22 de nuestro juego simulador de vuelo.... la punta del avion esta en el eje z positivo, su ala derecha al eje x positivo, y el parte superior del ala de atras del avion apunta al eje y positivo. ok? De momento tenemos que las coordenadas del objeto correspondenden con las coordenadas de nuestro mundo, no? hasta aqui bien.

Si rotamos el avion 90 grados sobre el eje Y, la punta del avion apuntaria al eje X positivo, y el ala derecha al eje Z negativo. El ala de atras seguiria mirando hacia arriba, el eje Y positivo. En este nuevo punto rotamos el avion sobre el eje Z. Si tus transformaciones son correctas el F22 estara rotando sobre su propio eje Z. Si no has calculado bien probablemente tu avion estara girando sobre el eje Z del mundo.

Para no machacarnos la cabeza con este tipo de transformaciones (que empiezan a ser complicadas cuando las coordenadas del modelo no corresponden con las del mundo) debemos usar lo que se llaman Matrices. Si le damos a Direct3D matrices para trabajar, el hara todas las transformaciones del modo correcto, no como nosotros :)

Matrices

Las matrices son arrays triangulares de 4x4. Una matriz-mundo contiene cuatro vectores, que representan las coordenadas del espacio-mundo:

ux uy uz 0
vx vy vz 0
wx wy wz 0
tx ty tz 1

Los vectores u,v y w representan lo que se llama "cuerpo rigido". Esta es la matriz que define la transformacion desde el espacio-modelo al espacio-mundo. Graficamente quedaria asi:

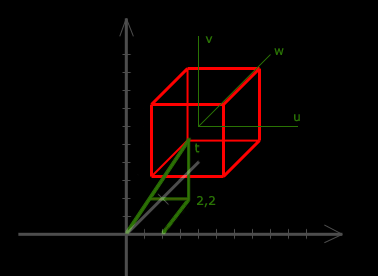
Para describir la posicion del cubo, la matriz seria esta:

1, 0, 0, 0
0, 1, 0, 0
0, 0, 1, 0
2, 2, 2, 1

Como el cubo esta orientado en el sistema de coordenadas, la primera columna contiene las coordenadas del espacio-mundo del eje x local, la segunda contiene el eje local y, y la tercera el eje z. Las vectores son vectores unitarios, es decir, que su magnitud es 1. La ultima fila contiene las coordenadas del espacio-mundo del origen del objeto.

La matriz identidad

1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

La matriz identidad es una identidad que representa un sistema de coordenadas orientado con las coordenadas del mundo. La coordenada X de la X local es 1; la Z y la Y de la X local son 0, y el vector de origen es (0,0,0). Asi que el eje x del modelo local encaja perfectamente con el eje x del mundo. Lo mismo ocurre con los ejes locales X y Z.

Pero bueno, que me estoy rayando... volvamos a lo que interesa: Si la posicion de un objeto en el espacio-modelo corresponde con su posicion en el espacio-mundo, entonces la matriz de transformacion del mundo sera la matriz identidad.

En Direct3D se puede acceder a esta y otras matrices de este modo:

D3DMATRIX mat;
mat._11 = 1.0f; mat._12 = 0.0f; mat._13 = 0.0f; mat._14 = 0.0f;
mat._21 = 0.0f; mat._22 = 1.0f; mat._23 = 0.0f; mat._24 = 0.0f;
mat._31 = 0.0f; mat._32 = 0.0f; mat._33 = 1.0f; mat._34 = 0.0f;
mat._41 = 0.0f; mat._42 = 0.0f; mat._43 = 0.0f; mat._44 = 1.0f;

La unica operacion matematica que vamos a ver es la multiplicacion. Un motor de representacion suele multiplicar un vector (que representa datos 3D, como un vertice o una normal) por una matrix 4x4. El resultado es el vector transformado:

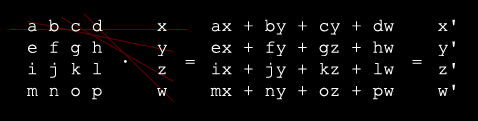
Antes de que un vector se transforme, debes construir la matriz de transformacion primero. Esta matriz indica como se va a convertir el vector a las nuevas coordenadas. Asi cualquier accion (escalar, rotar, trasladar, ...) requiere una matriz que debera ser aplicada al vector. Esas matrices se pueden multiplicar entre si para generar una unica matriz que contiene el resultado de las otras. Esta es la que llamamos matriz de transformacion.

Direct3D maneja internamente la concatenacion de estas matrices.

La Matriz Mundo

Un ejemplo tipico de matriz mundo seria una combinacion de matrices de traslacion, rotacion y escalado de objetos...

struct Object
{

	D3DXVECTOR3 vLoc;
	D3DXVECTOR3 vR;
	FLOAT fR, fG, fB;
	D3DMATRIX matLocal;
};
...

class CMyD£DApplication : public CD3DApplication
{
	...
	Object m_pObjects[NUM_OBJECTS];
	...
};

// en FrameMove()
for (WORD i=0; i<dwnumberofobjects; i++)
{
	D3DXMATRIX matWorld;
	D3DXMatrixTranslation(&matWorld, m_pObjects[0].vLoc.x, m_pObjects[0].vLoc.y, m_pObjects[0].vLoc.z);
	D3DXMATRIX matTemp, matRotateX, matRotateY, matRotateZ);
	D3DXMatrixRotationY( &matRotateY, -m_pObjects[0].vR.x );
	D3DXMatrixRotationX( &matRotateX, -m_pObjects[0].vR.y );
	D3DXMatrixRotationZ( &matRotateZ, -m_pObjects[0].vR.z );
	D3DXMatrixMultiply( &matTemp, &matRotateX, &matRotateY );
	D3DXMatrixMultiply( &matTemp, &matRotateZ, &matTemp );
	D3DXMatrixMultiply( &matWorld, &matTemp, &matWorld );
	m_pObjects[0].matLocal=matWorld;
}

// en Render()
for (WORD i=0; i<dwnumberofobjects; i++)
{
	...
	m_pd3dDevice -> SetTransform(D3DTS_WORLD, &m_pObject[i].matLocal );
	...
}

Nota:: Las matrices se deben multipiclar segun un orden. No es lo mismo multiplicar a por b, que b por a.
El orden correcto para multiplicar nuestras matrices es:

| W | = | M | * | T | * | X | * | Y | * | Z|

donde M es la matriz-modelo, T es la matriz-traslacion, X Y Z son las matrices de rotacion

El codigo que he escrito antes taslada el objeto a su lugar con D3DXMatrixTranslation(). Podemos decir que se trata de un cambio linear en la posicion. Este cambio se puede representar como un vector delta [ tx, ty, tz ]

Despues en el ejemplo lo que hacemos es rotar el objeto. Se trata de un movimiento circular alrededor de un eje.

Por ultimo lo que hemos hecho ha sido multiplicar las matrices con D3DXMatrixMultiply() para obtener una sola

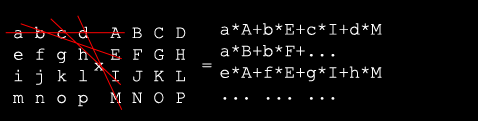
Una vez que ya tienes la matriz de transformacion, necesitas llamar a SetTransform() para aplicarla.

La Matriz Vista

Esta matriz describe la posicion y la orientacion de la camara desde la que se ve la escena. Es decir, tu detras del monitor :)

Para especificar la vista necesitamos tres vectores: UP, RIGHT, LOOK

El vector UP nos indica donnde es arriba para la camara. Suponiendo que en estos momentos tu eres la camara, UP seria un vector que apuntase al techo.
El vector RIGHT indicaria a tu derecha, y sirve para indicar la orientacion de la camara.
El vector LOOK apuntaria a cualquier parte de la pantalla, nos indica hacia donde esta mirando

Rotar la camara sobre un eje

Para visualizarlo imaginate nuestro avion F22. si te sientas al volante y pulsas el pedal de izquierda/derecha.....los vectores RIGHT y LOOK se deben rotar alrededor del vector UP. (rotar sobre el eje Y se llama efecto YAW)
Ahora, si pulsas estas volando y te inclinas hacia la izquierda o hacia la derecha ... los vectores RIGHT y UP se deben rotar alrededor de LOOK. (rotar sobre el eje Z se llama efecto ROLL).
Por ultimo, si inclinamos el avion hacia delante y atras, estariamos rotando el vector LOOK y UP sobre RIGHT (rotar sobre eje X se llama PITCH)

Con nuestra matriz-Vista podemos situar la camara donde queramos del espacio 3D y rotarla en cualquiera de los ejes para poder hacer nuestro juego.

Ahora bien, existe un pequeño "pero". Cuando realizamos muchas operaciones con comas (numeros flotantes) se van acumulando pequeños errores que hacen que nuestra camara se deforme. Estos errores basicamente hacen que los tres vectores que definen nuestra camara, tras varias rotaciones, dejen de ser perpendiculares entre si. Una cosa que no habia dicho es que estos tres vectores que usamos para la matriz-Visa deben ser siempre perpendiculares entre si :)

Este "defecto" es conocido como "drifting". Y para corregirlo hay que usar el siguiente codigo:

static D3DVECTOR vLook=D3DVECTOR(0.0f, 0.0f, -1.0);
static D3DVECTOR vUp=D3DVECTOR(0.0f, 1.0f, 0.0f);
static D3DVECTOR vRight=D3DVECTOR(1.0f, 0.0f, 0.0f);
D3DXVec3Normalize(&vLook, &vLook);
D3DXVec3Cross(&vRight, &vUp, &vLook);
D3DXVec3Normalize(&vRight, &vRight);
D3DXVec3Cross(&vUp, &vLook, &vRight)
D3DXVec3Normalize(&vUp, &vUp);

A ver, que hemos hecho aqui arriba? pues muy sencillo, lo primero es normalizar el vector LOOK. Normalizar significa simplemente poner su longitud a 1. Los vectores que tienen como longitud se llaman "unitarios" o "normalizados". Para calcular un vector normalizado se divide el vector por su longitud (o magnitud, es lo mismo). Y para calcular la magnitud del vector se usa el teorema de pitagoras:

magnitud = raiz cuadrada de (x_ + y_ + z_)

La funcion D3DXVec3Normalize() hace estos calculos por nosotros, asi que no hace falta preocuparse por las matematicas de momento, era solo para asustarte :)

Una vez que hemos normalizado el vector LOOK, creamos el vector RIGHT haciendo el producto de UP y LOOK. Cuando multiplicamos dos vectores obtenemos un tercer vector que es perpendicular a los primeros. Este calculo lo hacemos con la funcion D3DXVec3Cross() asi que tampoco hace falta crearnos nuestra funcion matematica de momento.

El producto de vectores es util no solo para corregir el drifting, sino tambien para saber que caras estan mirando hacia la camara. Si usamos dos lados cualquiera de un poligono y los multiplicamos, obtenemos un vector perpendicular, es decir... su normal. (las normales estan explicadas en el primer tutorial). Pero esto de momento es solo para que te suene.

>Y ahora que tenemos ya los 3 vectores perpendiculares, que hacemos con ellos??

pues lo siguiente es construir las matrices para rotar la camara.... pitch, yaw y roll, recuerdas?

D3DXMATRIX matPitch, matYaw, matRoll;
D3DXMatrixRotationAxis(&matPitch, &vRight, fPitch);
D3DXMatrixRotationAxis(&matYaw, &vUp, fYaw);
D3DXMatrixRotationAxis(&matRoll, &vLook, fRoll);

Multiplicando por ejemplo la matriz matYaw con los vectores LOOK y RIGHT, podemos rotar dos vectores sobre el otro.

D3DXVec3TransformCoord( &vLook, &vLook, &matYaw );
D3DXVec3TransformCoord( &vRight, &vRight, &matYaw); 

D3DXVec3TransformCoord( &vLook, &vLook, &matPitch );
D3DXVec3TransformCoord( &vUp, &vUp, &matPitch);
  
D3DXVec3TransformCoord( &vRight, &vRight, &matRoll );
D3DXVec3TransformCoord( &vUp, &vUp, &matRoll );

Y ya por fin! creamos la matriz-vista...

D3DXMATRIX view=matWorld;
D3DXMarixIdentity( &view );
View._11 = vRight.x; View._12 = vUp.x; View._13 = vLook.x;
View._21 = vRight.y; View._22 = vUp.y; View._23 = vLook.y; 
View._31 = vRight.z; View._32 = vUp.z; View._33 = vLook.z; 
View._41 = - D3DXVec3Dot( &vPos, &vRight );
View._42 = - D3DXVec3Dot( &vPos, &vUp );
View._43 = - D3DXVec3Dot( &vPos, &vLook ); 
m_pd3dDevice -> SetTransform( D3DTS_VIEW, &view);

de un modo grafico:

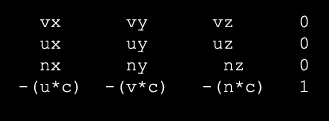
En esta matriz: u,n y v son UP, RIGHT y LOOK. Y c es la posicion de la camara en el mundo.
Esta posicion se calcula negando el producto entre la posicion de la camara y los vectores u,v y n. Se niegan porque la camara trabaja es sentido contrario al mundo 3D.

Asi, para rotar dos vectores sobre otro, simplemente cambiamos el valor de fPitch, fYaw y fRoll:

fPitch=- 0.3f * m_fTimeElapsed;
   ... 
   fPitch =+ 0.3f * m_fTimeElapsed;
   ... 
   fYaw =- 0.3f * m_fTimeElapsed;
   ... 
   fTaw =+ 0.3f * m_fTimeElapsed;
   ... 
   fRoll =- 0.3f * m_fTimeElapsed;
   ... 
   fRoll =+0.3f * m_fTimeElapsed; 
   ... 

la variable TimeElapsed sirve para sincronizar el movimiento. lleva cuenta del tiempo que ha transcurrido en el programa y asi en cada frame la variable se incremente un poco mas.

La cuarta dimension: Quaterniones

Si no te gusta todo el rollo este de las matrices, puedes usar otra tecnica que se llama "Quaterniones" para el movimiento de la camara. Un monton de juegos 3D usan esta tecnica, quizas el mas conocido es Tomb Raider. Esta tecnica da una sensacion de vista en tercera persona de nuestro mundo 3D.

La ventaja de usar Quaterniones es que requieren menos calculos y por ello el movimiento de la camara es mas suave. Se suelen usar tambien para animacion de esqueletos, cinematica inversa, fisicas 3d, etc

Basicamente consiste en añadir una cuarta dimension a la rotacion.

No, no estoy de cachondeo, jejeje :) a ver que me explique:

Hasta ahora hemos usado lo que se llama "vectores libres" de magnitud 1 que tenian 3 componentes (x,y,z). Ahora vamos a usar quaterniones, que tienen 4 componentes (x,y,z,w).

Veamoslo de otro modo:

Si nos dan el angulo y el eje, estos serian los componentes del quaternion...

x = Xa sen ( G / 2 )
y = Ya sen ( G / 2 )
z = Za sen ( G / 2 )
w = cos ( G / 2 )

Para rotar un vector un angulo de 2G sobre un eje u usando un quaternion, deberiamos poner las coordenadas de un vector p = (px, py, pz, pw) en los componentes de un quaterion v, suponiendo ademas que tenemos un quaternion q unitario q = ( senG u, cosG ).

Es decir:

v' = q v q^-1

rota v sobre el eje y, un angulo de 2G.

el vector v' que se obtiene tendra siempre un valor escalar 0 para la componente w, asi que lo puedes omitir para los calculos.

La rotacion que hemos hecho aqui es parecida a si nos moviesemos alrededor de una gran mesa de billar.

>ok tio, pero a ver como ostias programo yo toda esta matematica en mi programa!!!!

pues esta un poco dificil, porque Direct3D (ni otras APIs como OpenGL) no soportan directamente quaterniones.
La respuesta es:

- Convertir el angulo a quaterniones
- y convertir de quaterniones a matices.

No te asustes porque es mas sencillo de lo que parece, simplemente hay que seguir estos pasos:

1. Trasladar el vector vTrans (el que marca la posicion de la camara y el punto sobre el que rota)
2. Construir el quaternion usando los angulos que nos devuelve D3DXVECTOR3 al rotar la camara.
3. Construir la matriz a partir del quaternion
4. Concatenar la matriz con la matriz-posicion
5. Invertir la matriz-posicion a la matriz-vista

Aqui tienes el codigo que hace todo esto:

D3DXVECTOR3 vTrans( 0.0f, 0.0f, 0.0f );
D3DXVECTOR3 vRot( 0.0f, 0.0f, 0.0f );


// segun la tecla pulsada...
if( m_bKey[VK_HOME] )		vTrans.z += 0.2f; // Mover hacia adelante
if( m_bKey[VK_END] )		vTrans.z -= 0.2f; // Mover hacia atras
if( m_bKey[VK_NUMPAD4] )	vTrans.x -= 0.1f; // deslizar izquierda
if( m_bKey[VK_NUMPAD6] )	vTrans.x += 0.1f; // deslizar derecha
if( m_bKey[VK_NUMPAD8] )	vTrans.y += 0.1f; // deslizar abajo
if( m_bKey[VK_NUMPAD2] )	vTrans.y -= 0.1f; // deslizar arriba
if( m_bKey[VK_UP] )			vRot.y += 0.1f; // Pitch hacia arriba
if( m_bKey[VK_DOWN] )		vRot.y -= 0.1f; // Pitch hacia abajo
if( m_bKey[VK_LEFT] )		vRot.x += 0.1f; // girar izquierda
if( m_bKey[VK_RIGHT] )		vRot.x -= 0.1f; // girar derecha
if( m_bKey['C'] )			vRot.z += 0.1f; // rotar izquierda
if( m_bKey['X'] )			vRot.z -= 0.1f; // rotar derecha


// fijar cfSmooth a 0.98
const FLOAT vfSmooth = 0.98f;


// velocidad de transformacion y rotacion
m_pVelocity = m_pVelocity * cfSmooth + vTrans;
m_pvAngularVelocity = m_pvAngularVelocity * cfSmooth + vRot;

//transformacion y rotacion
vTrans = m_pvVelocity * m_fTimeElapsed * m_fSpeed;
vRot = m_pvAngularVelocity * m_fTimeElapsed * m_fAngularSpeed;

//actualizar las matrices de posicion y vista
D3DXMATRIX matT, matR;
D3DXQUATERNION qR;
D3DXMatrixTranslation( &matT, vTrans.x, vTrans.y, vTrans.z );
D3DXMatrixMultiply( &m_matPosition, &matT, &m_matPosition );
D3DXQuaternionRotationYawPitchRoll( &qR, vRot.x, vRot.y, vRot.z );
D3DXMatrixRotationQuaternion( &matR, &qR );
D3DXMatrixMultiply( &m_matPosition, &matR, &m_matPosition );
D3DXMatrixInverse( &m_matView, NULL, &m_matPosition );
m_pd3dDevice -> SetTransform( D3DTS_VIEW, &m_matView );

D3DMatrixTranslation() construye una matriz, que translada n objeto a (x,y,z). Se multiplica esta matrix con la matriz actual de posicion usando D3DXMatrixMultiply(). Eso translada el vector que describe el punto de rotacion. D3DQuaternionRotationYawPitchRoll() construye un Quaternion con el Yaw, Pitch y Roll que le especificamos. Esta matriz se multiplica con la matriz de posicion usando D3DXMatrixMultiply().

Por ultimo calculamos la Matriz Inversa , por que? porque usamos un quaternion para rotar la camara. Estas rotaciones ocurren sobre un punto arbitrario, porque la camara se transladara a otros puntos donde ocurrira la rotacion. Una rotacion sobre un punto arbritario no sera linear si no invertimos la matriz de rotacion.

Ahora, aunque no haga falta saberlo.... que es lo que hace D3DMatrixInverse() ??

Loque hace es invertir el angulo de rotacion de la matriz de rotacion. Una rotacion sobre el origen a traves de un angulo "a" seria anulada por una rotacion a traves del angulo "-a". La inversa de una matriz se representa como A^-1 .... asi que tenemos:

(A) (A^-1) = (A^-1)(A) = I

Esto es, multiplicar la matriz A con su inversa da como resultado la matriz Indentidad, la recuerdas?

Resumiendo, invertir la matriz de rotacion se usa para mapear el origen de la rotacion sobre un punto arbitrario en si mismo. Y para obtener una transformacion lineas necesitamos invertir la matriz. tampoco hace falta que le des muchas vueltas :)

La matriz Proyeccion

Aqui no me voy a enrollar mucho porque esto ya se esta haciendo muy largo. Tan solo decir que la matriz de proyeccion es la que convierte el "frustum" (ese trozo de la vista con forma de cubo irregular, hay un dibujo mas arriba que lo explica) en una espacio cuadrado. Los objetos que estan cerca de la camara se hacen mas grandes, mientras que los otros se hacen mas peques.