New Insight on the Ninepoint Circle / Darij Grinberg
This note is an expansion of my Hyacinthos #6127, Part 2.
The "little" Feuerbach theorem, i. e. the fact that the midpoints of the sides and the feet of the altitudes of an arbitary triangle lie on one circle, is a quite simple theorem, and just this is the reason it can be proven in several ways, but the most proofs are essentially equivalent or similar. Here, I am going to show a proof which is somewhat shorter than the ones I have seen before.
Let ABC be an arbitary triangle. Denote by A', B' and C' the midpoints of segments BC, CA and AB. (See Fig. 1.) The triangle A'B'C' is called the medial triangle of triangle ABC. The ninepoint circle (or Feuerbach circle) of triangle ABC is defined as the circumcircle of the medial triangle A'B'C'. We have to prove that:
Theorem 1: The feet of the altitudes of triangle ABC lie on the ninepoint circle of triangle ABC.
Proof: By the mid-parallel theorem, we
have C'A' || CA and A'B' || AB. Thus, the
quadrilateral AB'A'C' is a parallelogram. Hence, ![]() B'AC' =
B'AC' = ![]() B'A'C'.
B'A'C'.
Now let X be the reflection of the
point A in the line B'C'. Then, ![]() B'XC' =
B'XC' = ![]() B'AC'. Together with
B'AC'. Together with ![]() B'AC'
=
B'AC'
= ![]() B'A'C', this
yields
B'A'C', this
yields ![]() B'XC' =
B'XC' = ![]() B'A'C'. Hence, by the
inscribed angle theorem, the point X lies on the circumcircle of
triangle A'B'C', i. e. on the ninepoint circle of triangle ABC.
B'A'C'. Hence, by the
inscribed angle theorem, the point X lies on the circumcircle of
triangle A'B'C', i. e. on the ninepoint circle of triangle ABC.
Before we continue the proof, we notice that B'C' || BC, and that the distance from the point A to the line BC equals twice the distance from the point A to the line B'C'. Both of these facts follow from the mid-parallel theorem.
 Fig. 1
Fig. 1  Fig. 1a
Fig. 1a
Now, what is the signification of the point X ? We have defined X as the reflection of the point A in the line B'C'. Thus, firstly, the segment AX is orthogonal to B'C', therefore orthogonal to BC (since B'C' || BC), and secondly, the distance from A to X is the double distance from A to B'C', consequently equal to the distance from A to BC. Hence, X is the foot of the A-altitude in triangle ABC (Fig. 1a). We have proven that the foot of the A-altitude lies on the ninepoint circle; similarly this is proven for the two other feet of the altitudes. This proves Theorem 1.
Theorem 1 shows, that six remarkable points lie on the ninepoint circle. We can also obtain three other well-known points on the ninepoint circle:
Theorem 2: If H is the orthocenter of triangle ABC, then the midpoints of segments HA, HB and HC also lie on the ninepoint circle.
Proof: This theorem follows from Theorem 1, applied to the triangles BHC, CHA and AHB. Actually, the ninepoint circle of BHC is identical with the ninepoint circle of ABC, because the feet of the altitudes of both triangle coincide (prove it!). This yields that also the midpoints of the sides of triangle BHC lie on the ninepoint circle of triangle ABC, i. e. the midpoints of segments BC, HB and HC. By considering triangle CHA we also see that the midpoint of segment HA lies on the ninepoint circle.
Now let's return to the configuration of Theorem 1. The ninepoint circle is the circumcircle of triangle A'B'C'; we also have looked at the circumcircle of triangle AB'C'. Now introduce the circumcircles of the two rest triangles BC'A' and CA'B' (Fig. 2 and Fig. 3). Altogether, we get four congruent circles (they are the circumcircles of the congruent triangles A'B'C', AB'C', BC'A' and CA'B'). We will proceed to show that they have a common point.
Note that this remains true also for arbitrary positions of points A', B' and C' on the sides of the triangle (Miquel theorem). In our case, we have:
 Fig. 2
Fig. 2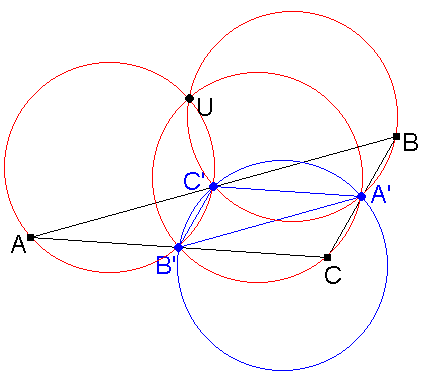 Fig. 3
Fig. 3
Theorem 3: If A', B' and C' are the midpoints of the sides of triangle ABC, then the circumcenter U of triangle ABC lies on the circumcircles of triangles AB'C', BC'A' and CA'B'.
The proof is very easy (Fig. 2a): Since U lies on the three perpendicular bisectors of triangle ABC, we have angle UC'A = 90° and angle UB'A = 90°, i. e. C' and B' lie on the circle having AU as diameters. Therefore, U lies on the circumcircle of triangle AB'C'; analogously, we show that U lies on the circumcircles of triangles BC'A' and CA'B'.
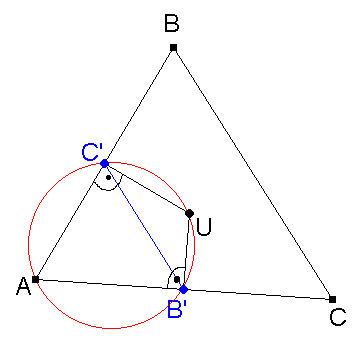 Fig. 2a
Fig. 2a
Now consider again the symmetry with respect to line B'C'. Each point of the circumcircle AB'C' is mapped to a point on the ninepoint circle. After Theorem 3, U lies on the cicumcircle of triangle AB'C'; thus, the reflection of U in B'C' lies on the ninepoint circle. The same holds for the reflections of U in C'A' and A'B'. We summarize:
Theorem 4: The reflection of the circumcenter U in the sides B'C', C'A' and A'B' of the medial triangle lie on the ninepoint circle of triangle ABC.
These are three further points on the ninepoint circle, and they seem to be little known points.
References
[1] H. S. M. Coxeter, S. L. Greitzer: Geometry Revisited.
New Insight on the Ninepoint Circle
HTML file
Darij Grinberg