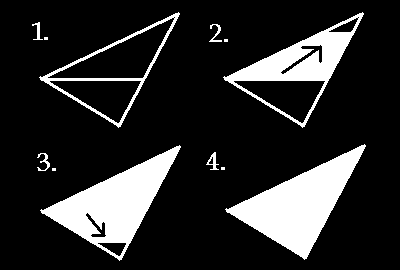
All polygons can be made of other polygons. Concave polygons can be made using two or more convex polygons. Convex polygons can be made and filled using triangles. So in order to fill any polygon, all that is needed is the ability to fill triangles.
There are two different types of fills that can be used. A polygon may be filled with a solid color or with a texture. The easiest to perform is filling with a solid color. A triangle may be filled with a solid color by drawing lines. The first step is to order the points of the triangles from up to down. Then the triangle is divided in two by a horizontal line. This line is determined by using the middle point's y-value and the line imbetween the first point and the bottom point. So the line that divides the triangle in two's endpoints are the middle point and the point where a line going through the middle point with a slope of 0 intersects the line passing through the top and bottom points which we will call point P.

Now that the triangle is divide into two triangle with horizontal lines, the change in y and the change in x need to be found from the line passing through the top and bottom points. Then you divide the change in x by the change in y which we will call m.
To fill the top half of the triangle you need to find the change in x and the change in y of the line passing through the top point and middle point. Then the change in x is divided by the change in y which we will call n. Start out by drawing a line from point P to the middle point. Then increase the y value by 1. If the middle point is on the left side of the line to point P, then increment the middle point's x-value by n and decrease point P's x-value by m. If point P is on the left side of the line to the middle point, then increase point P's x-value by m and decrease the middle points x-value by n. This is done until the y-value is equal to the y-value of the top point.
The same process is done for filling the bottom half except the y-value is decreased and n is equal to the change in x divided by the change in y of the line passing through the middle and bottom points.
There is a special case scenario that should be tested for before ordering the points from top to bottom. This special case is a triangle with a vertical line passing through the top and bottom points. A simple test can be made to determine if this scenario exists. The top point's y-value should be tested to see if it equals the bottom point's y-value. This triangle should be treated as one halve. A vertical line should be drawn from through the top and bottom points. The change in y should be divided by the change in x of the line through the top and middle points which we will call m. The change in y should be divided by the change in x of the line passing through the bottom and middle points which we will call n. Then the x-value should be incremented or decreased by one depending on the location of the middle point. The x-value of the top endpoint should be decreased by m and the x-value of the bottom endpoint should be increased by n. This process is repeated until the x-value equals the x-value of the bottom point.

Now that we can fill triangles with a solid color filling convex polygons is just a matter of dividing the area into triangles. The polygon is already listed in an array with the number of points. Use a FOR statement from the second point to the second to last point. This index value we will call i. Fill the triangle that is made with the first point, point i, and point i+1.
Backgrounds are important because they provide better visual quality to your game. In a 2D game a background is usually a large bitmap or something like a bitmap. A bitmap is basically a picture stored in a two-dimensional array. The trouble with bitmaps is that bitmaps can be accessed by the user and edited. The user could actually mess up the functionality of a game. To avoid this, the programmer should usually create their own format. A bitmap has a specific format that Windows uses. If a user attempts to open the programmer's own specific picture file, then Windows will have trouble reading and understanding the file. The only way you can edit the picture file though is with a drawing program. The programmer should usually in my opinion make their own drawing programs. Making your own drawing program allows you to have specific options that another program may not and it allows you to make your own formats.
When a player moves in a 2D game he moves around the background. Using this we know that all we need to draw is the background on the screen. Since the screen is a square or a rectangle, all we have to use to describe the part of background the user sees is four coordinates. The easiest way to fill a rectangle is to draw lines from the top to the bottom or from side to side. When drawing our own formatted picture file, we want to start in the upper left corner. Each index that represents a color is drawn on the screen with respect to where it exists in the array. But when doing this make sure you know how the language you are using handles the coordinates of arrays. In some languages, the first coordinate represents row and the other is column, but in other languages it is the first coordinate that represents column and the other represents row.
Drawing programs are simple programs that change a bitmap when the user presses a button. So the position of the cursor determines what part of the bitmap that is edited.

An advanced feature of drawing programs is fills. Since we have a coordinate system of integers, decimals do not exist in arrays. Areas do not have to be filled as triangles. When the button for a fill is used, the color that exists at the mouse's coordinates is recorded. For convenience we will call this the negative color. The filling color is painted at the mouses coordinates and is recorded in the array's respective coordinates. The coordinates around the array's position are tested to see if they are the same color as the negative color. If one of the coordinates is the same color then it is changed to the fill color. Also this position is recorded. If the color is not the same then nothing happens with that coordinate. When every coordinate around the initial coordinate has been tested, the coordinates around the new recorded coordinates are tested. The process repeats itself until everything is filled.
Fractals are images that if are magnified, they look the same. The whole is made of parts that are just like it. Fractals are important not only because they are cool but because they have practical uses. Drawing a life like tree in a drawing program can become boring and long. But a fractal may be used to draw it instead. Also textures can be created using fractals.
There are two ways to make fractals using computers and the L-System. The first involves strings. The L-System uses symbols to represent things and operations. For instance, "+" could represent rotating 90 degrees and "F" could represent a line. The beginning is usually a line which would be "F". If you wanted to add a line that was rotated by 90 degrees off the previous line, then you would substitute "F" for "F+F" keeping in mind that "+" means to rotate. Then "F+F" becomes "F+F+F+F". This can continue on forever.
The other method is to think of points and coordinates. These points and cooordinates are stored in an array. The original line's points are stored in the array. Then the operation is performed on the line. The new lines' points are stored and so is the step. The hard part is to find the algorithms to use to know where to start. If you do not use an algorithm to start where the newest points are then your operations will slow down greatly. The same lines will be stored each time and operated on over and over again. This consumes memory and time. There is no specific algorithm to use because each one differs with each operation. But you should start by examining the number of lines in each phase. Sketch your fractal out if you can't do it in your head. For safety you should put down the numbers of the lines in the first five phases. Then look at the differences between each phase. Look for a relationship between everything. If the number of lines the operation creates for every one line is x and the phase you are in is n, then there should be xn-1. This is only a suggestion and you may actually have to use an algorithm.
To receive a better explanation of fractals, try the link in MAIN.