





1000-Char. Description 5 Helpful Tutorials 12 Frequently Asked Questions
DOWNLOADING ASSAM-CALCU v3.1 WITH VFP-6 RUNTIME
To download and install Assam-Calcu (Assam-Calcu: A Programmable All-Purpose Calculator), an end-user must agree to its End-User License Agreement (EULA). You may click here to access that EULA: if you are an prospective end-user please take care to go through it.
Click
here to download
Assam-Calcu v3.1 inclusive of Visual FoxPro 6 Runtime
(packaged as a win-zipped file ACalc3p1Setup.zip of size ~3.3 MB: if you do
not already have a zip utility, may visit
winzip.com).
Assam-Calcu v3.1/ v3.0 is being hosted/ listed/ awarded by many software
archives on the web, including the coveted download.com:




![]()
![]()


Assam-Calcu is a 12-digit
multi-purpose calculator that can store and recall millions of your old
calculations - whether ordinary or scientific. It may also be easily programmed
to run hundreds of calculation-steps in one go. It is designed to be equally
convenient for purposes as varied as the simplest grocery arithmetic as well as
the most advanced technological computations.
The basic operation in Assam-Calcu is execution of a simple command-line (say,
'Answer = 673+245'), of which the left side is a variable (say, 'Answer'), and
on the right side of which lies an expression (say '55*4' or 'Mass*(3.0E8)**2').
If the right side uses one or more variable(s), e.g., 'Mass', their values must
have been defined in earlier steps. Compared to most calculator-instruments, Assam-Calcu
offers the much wider range of 9.9E+300 to 1.0E-300 for its results. It also
contains a database of values for popular constants & conversion-factors.
Versions 3.x allow definition of several pre-defined SI-unit constants in one go.
This Windows software (screenshot shown below) has been developed by Rituraj Kalita, a resident of Guwahati, Assam (India) first during December, 2006 (using the Visual FoxPro 6 platform), and is being distributed as a freeware (i.e., free software) by Eastern Star Software, Guwahati.
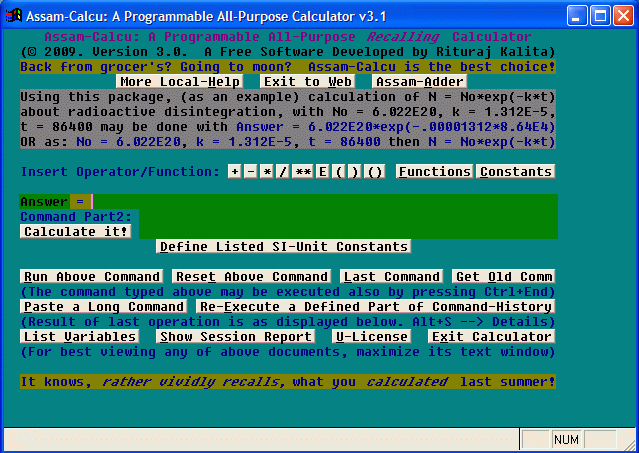
Fig.: Assam-Calcu Screenshot
Now, please do spare a few more minutes to go through the following 'Tutorials' and 'Frequently Asked Questions'!
1. Personal Grocery Calculations in an
Indian Town:
Suppose someone in a small town in India has just bought from the
local grocer's some 5 kg of rice at Rs. (i.e., Indian Rupees) 15 per kg, 2 kg of
potato at Rs. 8 per kg, 1.5 kg of lentil (masur dal) at Rs. 28 per kg, and half
a kg of onion at Rs. 15 per kg. To calculate this, proceed as follows:
double-click at the Assam-Calcu desktop-icon to run, then click at
the 'Reset Above Command' button just ONCE to clear the right side of the
command, then type (on that right side) 5*15 + 2*8 + 1.5*28 + 0.5*15 (so as to
represent above calculation; you may also add there a subsequent comment, say:
&& rice, potato, lentil, onion respectively. Press Ctrl+End (or press Alt+R or
click at the 'Run Above Command' button) to run this command. The result (140.5)
will be displayed, and the command with the result will remain stored forever
(may be recalled anytime later with just a button-click at the 'Get Old Comm'
button)!
2. Calculation of the Translational
Partition Function of a Given Volume of a Particular Gas Kept at a Given
Temperature:
In chemistry, one needs to calculate the translational partition
function (q_tr) of a gas-system using relation: q_tr = (((2*pai*m0*k*T)**1.5)/(h**3))*V,
where pai is 3.1416, m0 is the mass of a gas molecule equaling Mm/Na (where Mm
is the molar mass and Na is the Avogadro number), k is the Boltzmann constant, T
is the Kelvin-scale temperature, h is the Planck constant and V is the volume of
the system. For oxygen gas (molar mass 0.032 kg/mol) enclosed in a container of
volume 0.005 cubic meter at 27 Centigrade temperature (i.e., at 300.15 Kelvin),
we may proceed as (knowing that Na is 6.022E+23, k is 1.381E-23 J/(K-mol) and
that h is 6.626E-34 J-s): (i) Click twice at 'Reset Above Command' button to
clear the old command (ii) Enter & Run the following commands one by one: pai =
3.1416, Mm = 0.032, Na = 6.022E+23, m0 = Mm/Na, k = 1.381E-23, T = 300.15, h =
6.626E-34, V = 0.005 and then finally q_tr = (((2*pai*m0*k*T)**1.5)/(h**3))*V
(iii) In that final step you've got the result 8.84909618558E+029,
haven't you?
Note: (i) Most of the scientific
calculators (i.e., the instrument, not a software) won't be able to directly
find h**3, as it is (in the popular SI unit) less than 1.0E-100. (ii) Performing
this multi-step calculation in such a
simple non-programmable calculator instrument is as such quite a
cumbersome job (even if there arises no problem about the h**3
calculation)! (iii) To get the above steps in the form of a (FoxPro/
Visual-FoxPro) program-listing, re-run the above command steps again
using an Assam-Calcu Re-Run command, as explained in the 4th tutorial
below. (iv) The values of the above constants p, k, R, NA,
T, h etc. (in SI unit) may also be easily brought onto the command-line
by clicking at the Constants
button, and then by clicking at the entry for the desired (pre-defined) constant.
This inbuilt list of constants & conversion factors has been carefully
collated (for the physical-science constants are used the 2006 CODATA
recommended values) with help from some standard resources, as detailed here.
(v) To find q_tr for nitrogen gas (Mm = 0.028) enclosed
in 0.01 cubic meter volume at 325 K temperature, may now just run
(one by one) Mm = 0.028, m0 = Mm/Na, T = 325, V = 0.01 and
then q_tr = (((2*pai*m0*k*T)**1.5)/(h**3))*V
(the value thus obtained is 1.63214414284E+30, isn't it?)
3. Exact Calculation of the Constant in
the Wien's Displacement Law (in Physics) about Black-Body Radiation (Using an
Iterative Method):
While deriving the Wien's displacement law (regarding the
wavelength for the most intense radiation) from the Planck's law about
black-body radiation, it is found that the Wien's constant b equals (hc/yk),
where h is the Planck constant, c is the speed of light in vacuum, k is the Boltzmann constant, and y is
the numerical solution of the transcendental equation y*exp(y)/(exp(y)-1) = 5,
or in other words, of the equation y = 5 - 5*exp(-y). The
iterative method for solution of this equation has a fast convergence, and so
starting with a suitable approximate value of y (say, 5) we may continue
iterations using this relation y = 5 - 5*exp(-y). To perform these steps here, we start by running the command y = 5
and then the command y = 5 - 5*exp(-y). After this, we need
to just press Ctrl+End again and again to run this same command repeatedly. We
see that just with 8 steps, the value of y accurately converges to
4.96511423174, giving the value of the constant b as 0.00289707766 meter
Kelvin (using c = 2.998E+8 as the speed of light).
Note: Similarly, you may easily
solve the equation y = cos(y), starting with y = 0, reaching the
solution y = 0.73908513322 in 74 steps -- yet within a
duration of at most two minutes.
4. Using Gauss-Seidel Iteration Method
for Solution of a System of Linear Equations in Several Unknowns, via
Assam-Calcu 'Re-Run' Command:
Let us now solve the set of three linear equations
(x -2*y + 3*z = 10, x - 3*y + 2*z = 1, 3*x + y - z = 8) in the three unknowns
(x, y, z) by using the Gauss-Seidel iterative method. As per the well-known
process of judging the absolute values of the coefficients, we re-arrange the
above set as: (3*x + y - z = 8, x - 3*y + 2*z = 1, x - 2*y + 3*z = 10) and then
proceed to iterate using the following (equivalent) relations: x = (8 - y +
z)/3, y = (-1 + 2*z + x)/3, z = (10 - x + 2*y)/3
Let us initialize all the variables as
0, and then proceed with iterations. So we first run the three commands x = 0, y
= 0, z = 0. Then we run the three commands x = (8 - y + z)/3, y = (-1 + 2*z +
x)/3, z = (10 - x + 2*y)/3 one by one.
After this, we go for the 'Re-Run
Part of Command-History' option (as we now have to just run the last three
commands, in a queue, again and again as per the prescription of the
Gauss-Seidel iteration method). So, now we click at the 'Re-Execute a Defined
Part of Command-History' button (or press the equivalent hotkey Alt+E). We now
find that the 'Wizard for Generation of the Re-Run = Commands Syntax' has
appeared. With the help of this wizard, we choose the command x = (8 - y + z)/3
as the starting command, then choose the command (i.e., the next to next
command) z = (10 - x + 2*y)/3 as the ending command, and then choose a halting
time of 1 (one) second between successive commands. Now we click at Finish, and
find that a Assam-Calcu 'Re-Run' command of the form 'Re-Run = Commands
ranging from number 00000017 to number 00000019 (total 003 commands) haltingly'
has appeared. We now click at the 'Run Above Command' button, and view the
halting display of the three answers (for the first iteration).
Again we are to click at the same button to see another set, then again another,
and so on -- till the values of the unknowns x, y & z become practically
steady! We thus find that after 35 number of re-run operations we arrive at the
following final values for x, y & z:
x = 3.00000000000, y = 4.00000000000,
z = 5.00000000000, which comprise just the exact solution; while only after
11 re-run operations the results are quite close to the exact solution, i.e.,:
x = 3.00010986025, y = 3.99943728401, z =
4.99958823593.
Note: To jot down on paper (or to copy into the clipboard)
the aforesaid multiple-variable values, it's advisable to click EITHER at the Show
Session Report button so as to open the Session
Report OR better at the List
Variables button to view just the present
values of the variables (i.e., of x, y & z).
5. Calculating (as per simple LCAO-MO
theory involving only an 1s-type AO-pair with a single orbital exponent variable
k) the internuclear potential energy U of hydrogen molecular ion (H2+
ion) as a function of its internuclear distance R:
As is nicely explained in Ch. 3 (Section: MO Theory of H2+
molecular ion) of Quantum Chemistry by Ira N. Levine (3rd Ed., Prentice Hall of India, New
Delhi, 2003), the internuclear potential energy U (which is
also the electronic energy including internuclear repulsion VNN) of
the ground electronic state of H2+ ion (as per the
aforesaid simple MO theory) is expressible by the following straightforward
relations:
Internuclear Potential Energy U =
(Haa + Hab)/(1 + Sab) + 1/R
where
Overlap integral Sab = (1 + k*R + k*k*R*R/3) *
exp((-1)*k*R)
Coulomb integral Haa = 0.5*k*k - k - 1/R + (k+1/R) *
exp((-2)*k*R)
Resonance Integral Hab = (-0.5)*k*k*Sab - k*(2-k)*(1+k*R)*exp((-1)*k*R)
[Here k is the optimum orbital exponent for a given distance R,
obtainable via variation theory using a computer-program such as the
one developed by this author and
freely available from his site (it is also included within the working
folder of Assam-Calcu). The program output displaying the (R, k) values ranging
from (0.4, 1.8327) to (8, 1.0000) in steps of 0.2 atomic unit (a. u.) in R is as
listed in the file
INPE_Res.txt.] It may be noted here that from the result of the above
straightforward calculation, pretty realistic values of the (equilibrium)
bond-length Re and equilibrium bond-dissociation energy De
for H2+ ion could be easily obtained.
To do this above calculation very
quickly using Assam-Calcu, first enter the commands R = 0.4 and k = 1.8327
therein. Then enter the above three expressions for Sab, Haa
and Hab one by one. Then enter the expression for U, getting hereby
the value of U for R = 0.4. Next, put R = 0.6 and the corresponding appropriate
value for k (it is 1.7262) into Assam-Calcu, and then just re-run the
last four commands (the appropriate re-run command may be generated by
invoking the corresponding wizard) for values of Sab, Haa,
Hab and U. The new value of U for R = 0.6 is thus obtained. Repeat
the above process (the same re-run command may be just recalled and used,
there's no need to invoke the wizard again) for all other values of R (up to
8.0) for which k is available in the aforesaid file-list.
Note:
To jot down current values of the variables (R, k, Sab, Haa,
Hab, U) better
click at the List
Variables
button.
B. Frequently Asked Questions:
01. I know that we may run
Assam-Calcu by double-clicking at the desktop icon named 'Assam-Calcu -
Prog-able All-P'. But in my case, where is that desktop icon?
I'm sorry that in your case the Assam-Calcu Installer was unable to copy
the shortcut (link) icon (file) to your Windows desktop -- for most of the
computers it succeeds! But you may easily do that yourself. To do this yourself,
open the working folder (e.g., C:\AssamCalcu), starting from, say, 'My
Computer'. From that working folder find and copy the link-file named
'Assam-Calcu - Prog-able All-P' (see picture of that link-file below), and then paste that
link-file to your 'Windows
desktop' to facilitate running the Assam-Calcu application in future.
![]()
02. I keep getting an error message:
'Row or column position is off the screen!' whenever I try to run (i.e.,
open) Assam-Calcu. Where is the problem?
Most probably your monitor (VDU) screen resolution (screen area in
Windows terminology) is not set to a level high enough (i.e., at least to a
level of 800 by 600 pixels). You may try improving this particular Windows
setting (via Control Panel - Display), or as a simpler option may also
try changing the aforesaid desktop-icon's properties to have Assam-Calcu
always run in 'full-screen (i.e., maximized) window' mode - this solution
also generally works.
03. Can't all such calculations be done via
writing some programs, say in FORTRAN or in BASIC?
Why not? But, is learning
full-fledged programming an easy job? Assam-Calcu resides in the
twilight zone, i.e., a no-man's-land, between Using a Calculator and
Doing Programming! So, it offers the benefits of programming even
to lay users with a very little knowledge of programming, and thus
slowly & unknowingly initiates people to the ideas and concepts
of computer-programming! [Also, besides, the less we talk about
the precision and the range of values for calculations in FORTRAN
or BASIC, the better it is!]
04. What? Can it also help us learn
computer-programming?
Surely. The more someone would use
Assam-Calcu, particularly via defining and manipulating
variables, the more would he or she feel at home with the basic ideas in
computer-programming. In fact, the 'Assam-Calcu
History Commands-Listing' obtainable from the Assam-Calcu 'History Re-Run'
command is itself almost a FORTRAN program!
05. May I add comments to a command so as
to annotate (mark) it?
Yes, surely. Just type an && sign
after the command, and type any comment portion beyond this
double-ampersand sign.
06. How to preserve a session report for
future reference?
The session report, ordinarily,
lasts only for the duration of the particular session. To
preserve it for future use, click at 'Session Report' to display the
same, then from File menu, click at 'Save As', then save this
report with a different name OR in a different folder. (Such a saved
report may be viewed with Notepad or with WordPad etc.)
07. Isn't there a difference between
integer and real variables, as in FORTRAN?
Thank God, there's none! (Have you
checked the tutorials?) In FORTRAN, if we write k =
1.381E-23, k will become simply zero. But NOT here. So, don't worry here
about this issue.
08. Should we write here 2 as 2.0, as in
old FORTRAN versions?
Not necessarily, again for the
same reason mentioned just above.
09. How to backup the command-history?
The command-history resides in the
file named Comm_Hist (exactly speaking, named Comm_Hist.dbf) in the working folder (generally,
the folder C:\AssamCalcu).
So, to backup the command-history, just backup this particular file (say, to a
removable pen-drive). When your hard-disk fails, first re-install Assam-Calcu,
then copy this file back into the Assam-Calcu working folder.
10. Why can't I change the
Assam-Calcu command-history? Can I renew (i.e., reset) it?
Why, history shouldn't be changed,
isn't it? But you may surely erase the entire command-history
at one go, if you really feel over-burdened with this heritage
of command-history! To do that, just delete the above-mentioned
file (Comm_Hist.dbf) - you'll see that
your command-history has been renewed, i.e., got reset.
11. Within the middle of a multi-step
calculation job, I unknowingly closed down Assam-Calcu! Without repeating
the earlier (i.e., already done) steps one by one, is there a faster way
through which I may recover the continuity of working on that multi-step job,
and then happily continue working on the remaining part of that calculation
project?
Yes, surely! In this situation, just generate (using the aforesaid wizard
for Re-Run syntax generation) the appropriate re-run command for
re-running the old commands of the lost last session in one go, and then just
run that re-run command. The automated re-running process would now take
only a few seconds. After that, you may happily continue working on the
remaining part of the long calculation project!
12. Why can't I exit from the calculator if
some report, data or help is being displayed?
Because someone may actually want
to only hide the display of that report etc., but may instead
unintentionally close the whole application! So, if you want to
exit from Assam-Calcu, first close any report (or data) window,
and then try to exit!
Cite use of this package as:
Assam-Calcu: A Programmable All-Purpose Calculator
3.1,
© 2009 Rituraj Kalita, Guwahati (India).
References:
See the inbuilt list of constants & conversion factors.