
|


It's very simple.
If you're going to think about it, our problem is just a matter of
converting the actual time to the angles that measure the rotation of
the hour, the minute, and the second hand. The hour hand makes a complete
revolution every 12 hours, the minute hand every hour, and the second hand
every minute. Thus, we need a function to find the angles of the three
hands given the time. Once we have the angles, we can use trigonometry to
draw the hands. We can draw simple hands or complex hands—anything we
want as long as we have the angles.

Getting the hour, the minute, and the second.
I know of two simple ways to get the hour, the minute, and the second,
each in its own variable. One is to extract the data from the string
returned by TIME$:
TimeNow$ = TIME$
Hour% = VAL(TimeNow$)
Minute% = VAL(MID$(TimeNow$, 3, 2))
Second% = VAL(RIGHT$(TimeNow$, 2))
|

The other technique is by using TIMER:
TimeNow& = TIMER
Hour% = TimeNow& \ 3600
Minute% = (TimeNow& \ 60) MOD 60
Second% = TimeNow& MOD 60
|

Take note that the variable I used to copy the value of TIMER
is in Long Integer format (instead of just Integer). Find the reason why?
 Now you know how to
extract those things. But that is not what we want. (Haha.) We still need
the fractional parts of their value. Why? If we just got the integral parts,
the clock hands will point at discrete directions. What I mean is, if the
time is 4:30, the hour hand will point at four, instead of between four and
five. See what I mean? So the correct code should be: Now you know how to
extract those things. But that is not what we want. (Haha.) We still need
the fractional parts of their value. Why? If we just got the integral parts,
the clock hands will point at discrete directions. What I mean is, if the
time is 4:30, the hour hand will point at four, instead of between four and
five. See what I mean? So the correct code should be:
' Calculate the time values
TimeNow% = TIMER
Second% = TimeNow% MOD 60
Minute! = (TimeNow% \ 60) MOD 60
Minute! = Minute! + Second% / 60
Hour! = TimeNow% / 3600
If Hour! >= 12 THEN Hour! = Hour! - 12
|

Here, we made the second value an integer value. If you want it to have
fractional values so that the second hand will move continuously instead of
jumping every second, you can do so. The reason why I made it that way is
so that we just have to update the clock display every second, instead of
continuously (which could be flickery).
 I've noticed that
there's no easy way to get the value for the minutes. I just made it so
that I extract the integer value and then I just add the fraction of the
minute depending on the second value. I've noticed that
there's no easy way to get the value for the minutes. I just made it so
that I extract the integer value and then I just add the fraction of the
minute depending on the second value.
 By the way, you may
notice that we reduced the hour value to 12-hour format instead of the
usual 24-hour format since the hour hand makes a complete revolution every
12 hours (actually, it won't really matter in some applications, but we
might use a specific range of angles through look-up tables and such...). By the way, you may
notice that we reduced the hour value to 12-hour format instead of the
usual 24-hour format since the hour hand makes a complete revolution every
12 hours (actually, it won't really matter in some applications, but we
might use a specific range of angles through look-up tables and such...).

Converting to the angles.
Now that we have the time values in their respective variables, we can now
find the angles corresponding to each value. For convenience, we'll
redefine the angular system so that 0° points up, to the 12 o'clock
position, and the angle values increase in the clockwise direction. So
90° points to the 3 o'clock position, 180° points at 6 o'clock, and
so on.
 I said that the screen
mode we should use is SCREEN 12. Well, I plan on not changing the screen
coordinate system, which is just like the Cartesian Coordinate System
flipped along the x-axis (i.e., the positive x direction goes to the right
and the positive y direction goes downwards). And I plan on using the
trigonometric functions to convert the angle to the appropriate rectangular
coordinates. So my x-coordinate function would be sine (with respect
to my choice of angular system) and my y-coordinate function would be
negative cosine. Figure out why. I said that the screen
mode we should use is SCREEN 12. Well, I plan on not changing the screen
coordinate system, which is just like the Cartesian Coordinate System
flipped along the x-axis (i.e., the positive x direction goes to the right
and the positive y direction goes downwards). And I plan on using the
trigonometric functions to convert the angle to the appropriate rectangular
coordinates. So my x-coordinate function would be sine (with respect
to my choice of angular system) and my y-coordinate function would be
negative cosine. Figure out why.
 With those things out
of the way, let's now proceed with the time-value-to-angle functions. By
simple computation, we find out that the hour hand moves 30° every
hour, while the minute and second hands both move 6° every minute
and every second respectively. So we just multiply their corresponding
unit interval angle with their values. We also convert the angles to
radians since we'll be using the trig functions. With those things out
of the way, let's now proceed with the time-value-to-angle functions. By
simple computation, we find out that the hour hand moves 30° every
hour, while the minute and second hands both move 6° every minute
and every second respectively. So we just multiply their corresponding
unit interval angle with their values. We also convert the angles to
radians since we'll be using the trig functions.
' Compute the angles (converted to radians)
HrAng! = .523599 * Hour!
MnAng! = .104720 * Minute!
ScAng! = .104720 * Second%
|

Voila! Now we're through getting the angles!

Displaying the clock.
The next process is to display the clock. What I'm going to do here is to
show a very simple display. The clock would be centered on the screen. It's
border will be a circle with a radius of 200 pixels. The hands will just be
lines radiating from the center, with the hour hand having a length of
120 pixels, the minute hand 180 pixels, and the second hand 190 pixels.
Our center pixel is (320, 240).
 To make sure that we
update the the clock every second instead of continuously, we just do a
looping check for the integral value of TIMER
and redraw the clock whenever the value changes. To make sure that we
update the the clock every second instead of continuously, we just do a
looping check for the integral value of TIMER
and redraw the clock whenever the value changes.
' Wait for a second to elapse
Timed& = TIMER
DO: LOOP UNTIL INT(TIMER) <> Timed&
|

Here is code to draw the hands given the angles:
' Compute the hands' endpoints
HrX% = SIN(HrAng!) * 120 + 320
HrY% = -COS(HrAng!) * 120 + 240
MnX% = SIN(MnAng!) * 180 + 320
MnY% = -COS(MnAng!) * 180 + 240
ScX% = SIN(ScAng!) * 190 + 320
ScY% = -COS(ScAng!) * 190 + 240
' Draw the hands
LINE (320, 240)-(HrX%, HrY%), 12
LINE (320, 240)-(MnX%, MnY%), 12
LINE (320, 240)-(ScX%, ScY%), 14
|

Why we still put the coordinates in their own variables will be apparent
when we update the clock. Before, we can update the clock, we need to erase
the hands first and it would be faster to erase the hands by redrawing over
them with the background color instead of doing a CLS.
 Here's the complete
program with all the parts added and combined: Here's the complete
program with all the parts added and combined:
Listing B3.1


' Initialization
SCREEN 12
' Clock border
CIRCLE (320, 240), 200, 9
' Previous hand positions
PHrX% = 320: PHrY% = 240
PMnX% = 320: PMnY% = 240
PScX% = 320: PScY% = 240
' Clock display loop
DO
' Wait for a second to elapse
Timed& = TIMER
DO: LOOP UNTIL INT(TIMER) <> Timed&
' Calculate the time values
TimeNow& = TIMER
Second% = TimeNow& MOD 60
Minute! = (TimeNow& \ 60) MOD 60
Minute! = Minute! + Second% / 60
Hour! = TimeNow& / 3600
If Hour! >= 12 THEN Hour! = Hour! - 12
' Compute the angles (converted to radians)
HrAng! = .523599 * Hour!
MnAng! = .104720 * Minute!
ScAng! = .104720 * Second%
' Compute the hands' endpoints
HrX% = SIN(HrAng!) * 120 + 320
HrY% = -COS(HrAng!) * 120 + 240
MnX% = SIN(MnAng!) * 180 + 320
MnY% = -COS(MnAng!) * 180 + 240
ScX% = SIN(ScAng!) * 190 + 320
ScY% = -COS(ScAng!) * 190 + 240
' Erase the previous hands
LINE (320, 240)-(PHrX%, PHrY%), 0
LINE (320, 240)-(PMnX%, PMnY%), 0
LINE (320, 240)-(PScX%, PScY%), 0
' Draw the current hands
LINE (320, 240)-(HrX%, HrY%), 12
LINE (320, 240)-(MnX%, MnY%), 12
LINE (320, 240)-(ScX%, ScY%), 14
' Save the hands' position
PHrX% = HrX%: PHrY% = HrY%
PMnX% = MnX%: PMnY% = MnY%
PScX% = ScX%: PScY% = ScY%
LOOP UNTIL INKEY$ = CHR$(27)
|

 Here's a sample output: I took this screenshot at around 10:15 pm.
Here's a sample output: I took this screenshot at around 10:15 pm.

A little bit of fancy.
That clock display looks very boring. Lets spice it up a little by adding
second tick marks on the border and by extending the hands in the other
direction by 30 pixels. Here's the revised code (I've highlighted the
changes):
Listing B3.2


' Initialization
SCREEN 12
' Clock border
CIRCLE (320, 240), 220, 9
FOR I% = 0 TO 59
Rads! = I% * 3.14159265# / 30
X1 = SIN(Rads!) * 200 + 320
Y1 = -COS(Rads!) * 200 + 240
X2 = SIN(Rads!) * 210 + 320
Y2 = -COS(Rads!) * 210 + 240
IF I% MOD 5 = 0 THEN
LINE (X1, Y1)-(X2, Y2), 11
ELSE
LINE (X1, Y1)-(X2, Y2), 9
END IF
NEXT
' Previous hand positions
PHrX1% = 320: PHrY1% = 240
PMnX1% = 320: PMnY1% = 240
PScX1% = 320: PScY1% = 240
PHrX2% = 320: PHrY2% = 240
PMnX2% = 320: PMnY2% = 240
PScX2% = 320: PScY2% = 240
' Clock display loop
DO
' Wait for a second to elapse
Timed& = TIMER
DO: LOOP UNTIL INT(TIMER) <> Timed&
' Calculate the time values
TimeNow& = TIMER
Second% = TimeNow& MOD 60
Minute! = (TimeNow& \ 60) MOD 60
Minute! = Minute! + Second% / 60
Hour! = TimeNow& / 3600
If Hour! >= 12 THEN Hour! = Hour! - 12
' Compute the angles (converted to radians)
HrAng! = .523599 * Hour!
MnAng! = .104720 * Minute!
ScAng! = .104720 * Second%
' Compute the hands' endpoints
HrX1% = SIN(HrAng!) * 120 + 320
HrY1% = -COS(HrAng!) * 120 + 240
MnX1% = SIN(MnAng!) * 180 + 320
MnY1% = -COS(MnAng!) * 180 + 240
ScX1% = SIN(ScAng!) * 190 + 320
ScY1% = -COS(ScAng!) * 190 + 240
HrX2% = -SIN(HrAng!) * 30 + 320
HrY2% = COS(HrAng!) * 30 + 240
MnX2% = -SIN(MnAng!) * 30 + 320
MnY2% = COS(MnAng!) * 30 + 240
ScY2% = -SIN(ScAng!) * 30 + 320
ScY2% = COS(ScAng!) * 30 + 240
' Erase the previous hands
LINE (PHrX2%, PHrY2%)-(PHrX1%, PHrY1%), 0
LINE (PMnX2%, PMnY2%)-(PMnX1%, PMnY1%), 0
LINE (PScX2%, PScY2%)-(PScX1%, PScY1%), 0
' Draw the current hands
LINE (HrX2%, HrY2%)-(HrX1%, HrY1%), 12
LINE (MnX2%, MnY2%)-(MnX1%, MnY1%), 12
LINE (ScX2%, ScY2%)-(ScX1%, ScY1%), 14
' Save the hands' position
PHrX1% = HrX1%: PHrY1% = HrY1%
PMnX1% = MnX1%: PMnY1% = MnY1%
PScX1% = ScX1%: PScY1% = ScY1%
PHrX2% = HrX2%: PHrY2% = HrY2%
PMnX2% = MnX2%: PMnY2% = MnY2%
PScX2% = ScX2%: PScY2% = ScY2%
LOOP UNTIL INKEY$ = CHR$(27)
|

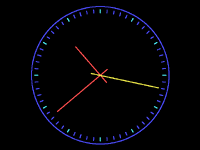 Here's the output to that program. The modifications I made to the program
deal with drawing the second tick marks around the border and the addition
of six new variables to track the position of the other endpoint of every
hand. Looks better, doesn't it?
Here's the output to that program. The modifications I made to the program
deal with drawing the second tick marks around the border and the addition
of six new variables to track the position of the other endpoint of every
hand. Looks better, doesn't it?
|
![[SEAV Softwares Logo]](../gfx/w_cologo.gif)
 Here's a sample output: I took this screenshot at around 10:15 pm.
Here's a sample output: I took this screenshot at around 10:15 pm. Here's the output to that program. The modifications I made to the program
deal with drawing the second tick marks around the border and the addition
of six new variables to track the position of the other endpoint of every
hand. Looks better, doesn't it?
Here's the output to that program. The modifications I made to the program
deal with drawing the second tick marks around the border and the addition
of six new variables to track the position of the other endpoint of every
hand. Looks better, doesn't it?