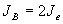2.1
Introduction:
In part 1 we unified the weak nuclear force with the electro-magnetic force.
In part 2 we shall unify the strong nuclear force with electro-magnetic force.
Since this unification relies upon many concepts discussed in my companion paper entitled Electrodynamic Space - Parts 1 & 2, the reader is urged to review that paper before continuing.
I shall use the acronym "EDS" (x.x.x) when referring to sections of the Electrodynamic Space paper.
The strong nuclear force is unique among the fundamental forces in several respects. Since it is this force that binds the atomic nucleus together in opposition to coulomb (electric) repulsion, it appears to be stronger than the electro-magnetic force. It's radius of interaction is approximately 10-15 meters, and beyond this distance the force of interaction is essentially zero. Strong nuclear force interactions are observed among hadrons (protons, neutrons, etc.) exclusively. 2.2.1
Electric field energy:
The electric field energy between two electric charges is defined by:
Where:
As can be seen from Eq. 1, the energy varies as the inverse of distance, and as the product term of electric charges Q1 & Q2, and as the inverse of the dielectric polarization of the medium (space) separating the charges.
It is this last term e0 (dielectric polarization) we shall focus upon.
Modern science assumes the value of e0 to be a constant. As I have shown in EDS (2.2.3), this is simply not true. In particular, when the electro-magnetic field energy approaches the dipole binding energy of space, the dielectric polarization value of space e0, becomes increasingly non-linear EDS (2.3.1), rising asymptotically and becoming effectively infinite at the breakdown potential of space. At moderate electro-magnetic field energies, the rise in e0 is less than a first order function of energy. However at high electro-magnetic field energies, the rise in e0 will be greater than a first order function of field energy. This last observation is crucial to understanding strong nuclear force interactions. 2.2.2
Proton-proton electric field energy:
Assuming a constant value for e0, the electric field energy of two protons, separated by one proton diameter is determined by:
Where:
The value so calculated for JP is: 2.898 x 10-13 Joules.
This may seem like a small amount of energy, but when calculated in terms of the electric field over a proton diameter, it represents a value in excess of 1019 Volts per meter!
2.2.3
Binding energy of space:
As shown in EDS (1.3.5 & 2.3.1), space itself will breakdown (ionize) at sufficiently high energy values.
The value is set by the binding energy of the dipoles (electron-positron pairs) that comprise space.
And since each observable electron has a mass equal to the energy required to liberate the particle from the Dirac sea, EDS (1.3.5) the binding energy of space is equal to twice the energy equivalence of the electron's mass, as shown in Eq.3.
Where:
The value so calculated for JB is: 1.637 x 10-13 Joules.
Please note, the value of JB is approximately 1.7 times smaller than the value of JP in Eq. 2 (above).
2.3.1
The breakdown of space:
As discussed in 2.2.1, the value of e0 becomes non-linear as electro-magnetic field energies approach the ionization energy of space.
Furthermore, as shown in 2.2.2 & 2.2.3, at the proton-proton separation distances encountered within an atomic nucleus, the inter-proton electric field energy is slightly greater than the ionization energy of space.
The situation is shown in figure 1.
Referring to Figure 1, as the inter-proton separation distance rP falls below 10-14 meters, the proton-proton electric field energy (JP) approaches the dipole binding energy of space, and the value of e0 starts to rise (the value of 1/e0 declines).
In other words, e0 no longer approximates a constant, but is instead a complex inverse function of inter-proton separation distance.
Since the value of JP it self varies as the inverse of e0 (Eq. 2), JP no longer rises linearly as inter-proton separation distance falls.
As inter-proton separation distance rP approaches 10-15 meters, the rate of change in e0 continues to accelerate, and eventually the ratio of change in e0 to change in separation distance rP exceeds unity (45 degree slope point of 1/e0 in figure 1) as shown by Eq. 4.
From this point onward, any further decline of inter proton separation distance rP results in a decline of proton-proton electric field energy.
In other words, proton-proton electric field energy is no longer an inverse relationship with rP, but instead directly proportional to inter-proton separation distance rP, and the protons are now bound together in an negative potential energy well.
These relationships are shown in Eq. 5.
Where:
The relationships of Eq.5 completely explain the inner workings of the strong nuclear force.
It's interaction distance is determined by the requirement that JP (Eq. 2) be approximately equal to JB (Eq. 3).
It is always an attractive force because within it's interaction distance, JP is directly proportional to rP (Eq. 5), and therefore proton-proton electric field energy actually rises with increasing inter-proton separation distance.
And finally, it is the precipitous decline in 1/e0 (Eq. 4) within the strong force interaction distance that creates the illusion of it's strength.
In other words, it is the breakdown of electrodynamic space that is responsible for the manifestation we call the strong nuclear force.
2.3.2
The strong nuclear force:
It is the extreme non-linearity of e0 (breakdown of electrodynamic space) caused by the proton-proton electric field energies encountered within the atomic nucleus that is responsible for creating the strong nuclear force (Eq. 5).
I have used proton-proton interactions in this discussion of the strong nuclear force, however it should be apparent that since neutrons are nothing more than a degenerate form of hydrogen (see The Unified Field - Part 1), therefore neutron-proton and neutron-neutron interactions will behave in an equivalent manner.
In one sense, Eq. 5 reduces the status of the strong nuclear force from that of a fundamental force, to that of a secondary effect, caused by a rather unique electro-magnetic interaction. In either case, we have now unified the strong nuclear force with the electro-magnetic force. 2.3.3
Nuclear decay:
The nuclear stability of an atom is a fragile balance among several competing phenomena.
In many respects, the nucleus of an atom behaves like a collection of marbles enclosed by a thin flexible membrane.
It could also be compared to an undulating droplet of water floating in zero gravity, where surface tension holds the droplet together.
In either case, so long as proton-proton coulomb repulsion is suppressed by the reduction of 1/e0 (breakdown of space), our nucleus remains intact.
There is one major flaw with the water droplet analogy. Unlike the water droplet which is composed of many trillions of atoms, the atomic nucleus is composed of a relatively small number of particles (< 240 for most atoms) and therefore the modes of vibration (undulations) are very constrained. High order harmonic vibration modes will result in small numbers of nucleons forming protrusions in the nuclear surface. If any of these protrusions becomes too pronounced, the inter-proton separation distance rP will exceed the constraint imposed by Eq. 4 (above). The result being an e0 slope < 45 degrees, and JP once more becoming an inverse function of inter-proton separation distance rP. At this point coulomb repulsion will reassert itself, and the protrusion will be ejected from the nucleus. Because anti-spin alignment between nucleon pairs results in lower overall nucleus energy, and degenerate hydrogen (neutron) electron orbit de-localization (1.3.4) also results in lower overall nucleus energy, it is only natural that many of these ejections (decays) will take the form of two protons and two neutrons. In other words, an alpha particle. Another common decay mechanism in heavy atomic nuclei is fission. A low order harmonic vibration mode will result in the nucleus adopting a "dumb bell" like shape at the peaks of this oscillation mode. When this vibration mode becomes too extreme, it is the "neck" between the two halves of the "dumb bell" that is most likely to exceed the rP constraint imposed by Eq. 4 (above). This form of decay generally results in two medium weight daughter atoms (the dumb bell ends), and multiple light weight fragments (the dumb bell neck). As nuclear weight rises, two effects become more influential, both detrimental to stability. First, the fundamental harmonic vibration mode of the nucleus is lowered, thereby coupling more efficiently to ambient thermal agitation. Second, the linear momentum contained in these low order harmonic vibration modes is larger, thereby producing greater stress within the "neck" of the "dumb bell". The combined result being an upper limit of approximately 240 nucleons for stable nuclei, with "islands" of nuclear stability beyond this limit, mainly caused by fortuitous higher order harmonic modes of oscillation partially disrupting the fundamental mode(s). 2.3.4
Astrophysical consequences:
It is a slow decline in the dielectric and paramagnetic polarization constants of space that is responsible for the expansion of the universe EDS (2.3.4).
This same decline plays a role in the evolution of matter as well.
The higher values of space polarization constants during the early evolution of the universe, imply a lower value for JB (2.2.1, 2.2.3 Eq. 3).
Which in turn implies a larger value for rP (2.3.1 Eq. 4 & 5) since the equilibrium point of JP to JB is shifted to a lower energy.
A larger value for rP means that many more atomic nuclei were stable during that early epoch of the universe than are stable today.
It is the narrowing boundaries of nuclear stability, resulting in wholesale nuclear decay, that created the awesome outpourings of energy we call quasars.
In other words, the universe is not only evolving at the level of stars and galaxies, it is also evolving at the subatomic level as well...
2.4.1
Summary:
The viewpoints and theories I have presented herein are in direct opposition to modern quark theory.
I make no apology for this.
Quark theory asserts that quark confinement is absolute, and no solitary quark can ever be observed.
To create a theory where by definition, the subject matter of that theory (quarks) can never be directly measured is akin to dogma, and therefore better suited to the realm of religious faith, than to serious scientific inquiry.
2.4.2
Conclusions:
That electric field energies encountered within the nucleus are of approximately the same magnitude as the binding energy of electrodynamic space, and therefore cause space it self to breakdown (2.2.1, 2.2.2, 2.2.3).
That a decline in the dielectric polarization constant of electrodynamic space 1/e0 is responsible for nuclear confinement, commonly known as the strong nuclear force (2.3.1).
That strong nuclear force interactions are in fact, a secondary effect of electro-magnetic force interactions (2.3.2).
That when viewed from the perspective presented herein, the phenomena surrounding nuclear stability and decay become an obvious and naturally occurring consequence of the nuclear confinement mechanism (2.3.3).
That certain astrophysical phenomena such as quasars result from a decline in nuclear stability caused by a slow change in rP over time (2.3.4).
In part 3, we shall consider some practical engineering examples.
End.
The Unified Field - Part 2
|
| Home |