... Sería una lástima revelar aquí esta sencilla técnica, negando a los lectores el placer de sentir su propia experiencia " ¡Ajá! ". Apenas puedo dar indicación alguna sin al mismo tiempo revelar la solución; baste decir que ésta puede enunciarse en una o dos frases, y que no requiere notación especial alguna. 

Hace tiempo que sentí la experiencia " ¡Ajá! " Y yo tampoco quiero privarte de la tuya, así que si lo deseas puedes dar un salto. 
La clave inicial está en la tabla en la tabla del Código Gray. 
En esta sección de Algoritmo Iterativo, también hago una diferencia, según la posición inicial del puzzle. Aquí si existen diferencias importantes, según que la Posición Inicial sea la Clásica o la Extrema. 
La Extrema es más sencilla de analizar y empiezo por ella. 

Posición Inicial Extrema 
Posición Inicial Clásica 
 
   
   
Posición Inicial Extrema 
Supongamos que el puzzle está en la Posición Inicial Extrema. 
 

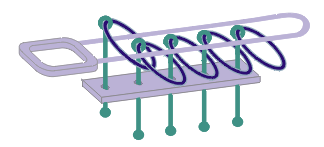Figura 17. Posición Inicial Extrema

No es difícil comprobar que el aro A se manipula de modo intermitente. Es decir, se manipula el aro A y luego se manipula otro aro. Así sucesivamente 
La primera manipulación es el aro A, meterlo (1). 
El problema es determinar ese otro aro, sin mirar la tabla. Sorprendentemente resulta que sólo existe un aro manipulable en cada estado. (excepto el aro A que acabamos de manipular) 
Repetimos el proceso. 
Manipulamos el aro A, sacarlo (0) 
Sólo podemos manipular el aro C, meterlo (1) 
Es una consecuencia directa de que el Código Gray sea cíclico. 
Repetimos el proceso hasta alcanzar La Posición Final, La primera en la tabla, con todos los aros libres. 
Así que no resulta complicado realizar un algoritmo iterativo de dos simples instrucciones para liberar los aros desde la Posición Inicial Extrema. 

Algoritmo Iterativo 10000 
Repetir: 

• Manipular el Aro A
• Manipular el Otro Aro Manipulable.

Algoritmo Iterativo 10000 
Repetir: 

• Manipular el único aro Manipulable, exceptuando el que acabamos de manipular.

EDCBA 
10110 

Quizás resulte confuso inicialmente, pero si no te interrumpen consigues solucionarlo sin tener que tomar ninguna decisión. 
Siempre existe sólo un aro manipulable. Podemos considerar que es un "Puzzle Lineal ", sin bifurcaciones entre la Posición Inicial Extrema y la Posición Final.  
Y mi pregunta clave es ... 
¿ Podemos considerar Los Aros Chinos un puzzle ? 
No lo sé, pero .... entonces ya me dio guerra antes comprender que no era un puzzle. 

Al igual que ocurría con el Cubo de Rubik si te interrumpían en medio de un operador, y no sabias dónde lo habías dejado, en los Aros Chinos ocurre igual. 
Supongamos que nos interrumpen cuando estamos realizando el Algoritmo Iterativo de dos instrucciones. 
Supongamos que dejamos el puzzle en una posición intermedia 

EDCBA 
01010 
 

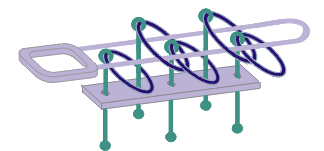Figura 18. Posición 01010

No sabemos cuál ha sido la última manipulación. 
Siempre existen dos manipulaciones posibles en las posiciones intermedias, en las posiciones extremas sólo existe una. 
Siempre es posible manipular el aro A. 
Luego siempre existe otro aro manipulable, que denomino en general El Otro Aro Manipulable  
No es necesario mirar la tabla, en la sección de Manipulación, se indica las condiciones para manipular un aro. Según la nomenclatura 

..X10..0  
..X1  

El aro X puede manipularse, se puede sacar o meter. Si recorremos los aros desde la derecha, el aro X es el siguiente al primer aro dentro (1). En el caso del ejemplo, C se puede meter. 
Nos fijamos en la tabla del Código Gray, según realicemos una manipulación u otra subimos o bajamos en la tabla. 

EDCBA 
01110 
01010 
01011 

En este caso: 
Si manipulamos A bajamos en la tabla, es decir nos alejamos de la solución. 
Si manipulamos C, El Otro Aro Manipulable, subimos, es decir, nos acercamos a la solución 
En otros casos ocurrirá al revés. Por ejemplo si la posición de la interrupción es la intermedia de la figura. 

EDCBA 
11011 
11010 
11110 

Si disponemos de la tabla, no existe ningún problema en determinar cual es la manipulación adecuada en una posición intermedia. 
Después podemos continuar con el Algoritmo Iterativo. 
Si NO disponemos de la tabla, el problema se complica. 
Si el código utilizado para la solución fuese el Código Binario Natural, sería sencillo conocer el estado de la fila anterior y determinar el aro a manipular. 
El Código Gray sabemos que el fácil construirlo, mediante el sistema de reflejar, pero es complicado determinar la fila anterior. Existe un sistema de conversión del Código Gray al Código Binario Natural, que es más o menos complicado, que podría solucionar el problema.  

He descubierto un sistema sencillo para determinar la siguiente manipulación que no requiere cálculos complicados. 
La clave está en que el aro A se manipula de modo intermitente. 
Exactamente cuando la posición del puzzle es impar en el Sistema Decimal. Se manipula en las posiciones 31, 29, 27 ... 
Sólo necesitamos conocer si una posición cualquiera es impar o par  

Si es impar, manipulamos el aro A. 
Si es par, manipulamos El Otro Aro Manipulable. 

Nos fijamos en una posición impar cualquiera, por ejemplo la 29. El número de aros dentro (1) es impar, 3 en este caso. 

10101 25 
10111 26 
10110 27 
10010 28 
10011 29 
10001 30 
10000 31 
EDCBA  

Al manipular cualquier aro y pasar a posición 28 par, el número de aros dentro (1) pasa a ser par, 2 en este caso. 
No importa que aro se manipula, ni el tipo de manipulación sacar o meter, la paridad del número de aros dentro será par. 
Concluyendo la paridad de una posición coincide con la paridad de los aros dentro (1) 
Entonces en la posición intermedia  

EDCBA 
01010 

Es una posición par, tenemos que manipular El Otro Aro Manipulable, aro C en este caso. 
 
 

Posición Inicial Clásica 
Veamos como diseñar un Algoritmo Iterativo para la Posición Inicial Clásica. 
Tiene más complicaciones, ya que es una posición intermedia y hay que asegurarse de que se realiza correctamente la primera manipulación. 
Tiene dos posibles manipulaciones, A o B 
Según elijas, subes o bajas en la tabla. 
En la Posición Inicial Clásica de 5 aros, ¿ Cuál es la primera manipulación ? 

EDCBA 
11111 
 

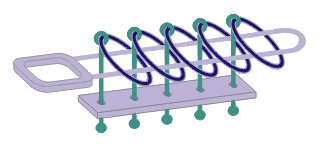Figura 19. Posición Inicial Clásica

Tiene 5 aros dentro, paridad impar 
Tenemos que manipular el aro A. 
El puzzle tiene según mi criterio una sorpresa oculta. 
¿ Cuál es el primer movimiento en la versión de 4 anillas ? 
Si no dominas el tema de los códigos binarios, elimina la columna E de la tabla del Código Gray y utilizar media tabla superior DCBA. 
Las Posiciones Iniciales Extremas, son todas impares, para un puzzle de N aros, la posición es: 

2^N -1. 
Para N=4, 15. 

Entonces, es válido el razonamiento realizado en la versión de 5 aros. 
La Posición Inicial Clásica en la versión de 4 aros, tiene 4 aros dentro, paridad par. 

DCBA 
1111 

Entonces tenemos que manipular EL Otro Aro Manipulable, el aro B. 
¿Sorprendido? 
¿ Cuál es la posición inicial más complicada, la Clásica o la Extrema ? 

Veamos entonces como diseñar un Algoritmo Iterativo para la Posición Inicial Clásica. 
Lo realizaré sólo para versión de 5 aros. 
El Algoritmo Iterativo de dos instrucciones, diseñado anteriormente para la Posición Inicial Extrema, sirve para esta posición, ya que la primera manipulación es idéntica, el aro A. 

Algoritmo Iterativo 11111 
Repetir: 

• Manipular el Aro A
• Manipular el Otro Aro Manipulable.

Algoritmo Iterativo 11111 

• Manipular el Aro A

Manipular el único aro Manipulable, exceptuando el que acabamos de manipular.