|
|
BAB 6 PEMBEZAAN DAN KAMIRAN LANJUTAN
6.1 Pembezaan Dan Kamiran Fungsi Trigonometri Songsang
Dalam
bahagian ini kita akan terbitkan rumus-rumus pembezaan bagi fungsi-fungsi sin-1x,
tan-1x dan sek-1x, manakala rumus pembezaan tiga fungsi yang lain boleh diperoleh daripada pembezaan tiga identiti berikut.
|
|
|
|
|
|
Dalam perbincangan seterusnya kita
memerlukan identiti berikut.
 |
6.1.1
Pembezaan y = sin-1x
|
|
6.1.2
Pembezaan y = tan-1x
|
|
6.1.3 Pembezaan y = sek-1x
|
|
6.1.4
Pembezaan y = kos-1x,
y = kot-1x dan y = kosek-1x
 |
Pada amnya jika u(x)
ialah fungsi dalam x maka diperoleh,
 |
6.1.5 Kamiran Melibatkan Fungsi Trigonometri Songsang
| Pembezaan | Pengamiran |
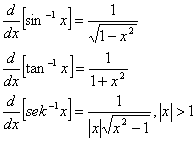 |
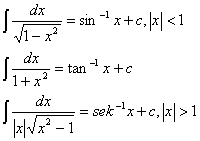 |
Contoh
6.2 Pembezaan Dan Kamiran Fungsi Hiperbolik Songsang
 |
Dalam bahagian ini kita akan terbitkan
rumus-rumus pembezaan bagi fungsi-fungsi sinh-1x, kosh-1x
dan tanh-1x, manakala rumus pembezaan tiga fungsi yang lain boleh
diperoleh daripada pembezaan tiga identiti berikut.
 |
6.2.1 Pembezaan y = sinh-1x
|
|
6.2.2 Pembezaan y = kosh-1x
|
|
6.2.3 Pembezaan y = tanh-1x
|
|
6.2.4 Pembezaan y = koth-1x, y = sekh-1x dan y = kosekh-1x
 |
Pada
amnya jika u(x) ialah fungsi
dalam x maka diperoleh,
 |
6.3 Penggunaan kamiran lanjutan.
6.3.1 Panjang Lengkung
(
i ) Bentuk koordinat Cartesan
|
|
|
|
( ii
) Bentuk parameter
|
|
|
|
| TUGASAN BKU KUiTTHO 2001. BVP. CHEE JUN WIE, KOK JIAN LING, LEE KOON MING |