Linear Transformations in Business
Eric Swanson
Matrix Theory can be used in a variety of applications. From physics to global positioning, linear algebra is used as an easy means of calculating extensive related equations. In economics, linear algebra is used extensively for managers to realize their maximum profits. One component of linear algebra is the study of linear transformation. This is important in economics because in manufacturing a manager can mathematically see how parts can be algebraically changed into actually products in the most efficient manner using linear transformation.
Linear transformation is defined as "a rule for changing one geometric figure (or matrix or vector) into another using a formula with a specified format."[1] This format must be a linear combination, in which the original components such as the coordinates of each point of the original figure are changed via the formula to produce the coordinates of the transformed figure.[2] Geometrically some examples of this include flipping the figure over the axis, stretching or compressing it, and rotating it.[3] It is also important to note that every such transformation has an inverse, which undoes its effect.[4] These points are good to understand when dealing with linear combinations.
In addition, other facts must
be revealed to fully understand the linear combination. A linear transformation
between two
vector spaces
V and W is a
map
such that the following hold:
1.
for any
vectors
and
in V, and
When V and W
have the same
dimension, it
is possible for T to be invertible, meaning there exists a
such that
. It is always the case that
.[6]
In the following picture different vectors are shown that have been transformed
by different addition and multiplication examples.
Now that the general understanding for linear transformation has been laid a further practical use needs to be presented. When presented equations like:
y1 = a11 x1 + a12x2 + a13x3
and
y2 = a21x1 + a22x2 + a23x3
Then those equations can be put into a matrix for further computation as such:
Thus the matrix A which
equals 
is said to be the object that transforms x into y.
In general, these matrix multiplications for linear transformations can be used to help mathematically bind information. The following two tables will show how with linear transformation, the two tables can relate and be understood. The first table deals with the different parts within different toys. The second table deals the different materials that go into those different parts. With a few matrix multiplication processes, the tables can be linear transformed and connected mathematically.
These transformations can be used in business to help keep track of the components used to make a product. In the following example a business manager making toys wants to know how much material used in each line of toys that he makes. He has accumulated the following data about his production:
Table 1. Parts Requirements for Toys (number of parts)[9]
|
Parts |
Type of Toys |
||
|
Toy 1 |
Toy 2 |
Toy 3 |
|
|
Part 1(Wheel) |
4 |
6 |
8 |
|
Part 2(Axles) |
2 |
2 |
3 |
|
Part3(Bodies) |
1 |
1 |
1 |
Therefore the total parts requirements can be stated in equation form as:
y1 = 4x1 + 6x2 + 8x3
y2 = 2x1 + 2x2 + 3x3
y3 = x1 + x2 + x3
Using matrix notation these equations are then made into:
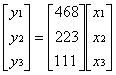or y = A x [10]
So therefore
the vector of toys is transformed into parts by the multiplication of A. Now to
further the understanding of this concept of x linearly transforming into y
another example will be added.
Now the company wants to know how much material is needed in each toy.
Table 2: Raw Materials Requirements For Parts (in Pounds)[11]
|
Material |
Type of Part |
||
|
Part 1 (Wheels) |
Part 2 (Axles) |
Part 3 (Bodies) |
|
|
Material 1 (Plastic) |
.5 |
0 |
3 |
|
Material (Steel) |
0 |
1 |
1 |
In this example, the matrix notation will be:
In the properties of linear combination, we are able to combine related matrices to combine them. Such as if y = Ax and x = Bw then y = ABw. This will be true for any vectors x, y, and w and any matrices A and B. So in following this in the example we get:
Now carrying out the matrix multiplication on the right side leads to:
Now this will give the amount of material in every toy. With this information he could calculate the cost of material per toy or many other things. Knowing linear transformation has helped this business manager know the amount of material in his line of toys.
The process to understand linear transformation is used in many applications such as business. Linear transformation is the idea of changing one vector to another by using a specified formula such as y = Ax. This can be a very practical tool within business to understand the relationships of how things are changed into another in the production of products.
[1]
Yahoo! Reference - The Britannica
Concise - linear transformation
<http://education.yahoo.com/search/be?lb=t&p=url%3al%2flinear_transformation>
20 Nov 2002.
[2] Ibid.
[3] Ibid.
[4] Ibid.
[5] Eric Weisstein. "Linear Transformation". World of Mathematics. <http://mathworld.wolfram.com/LinearTransformation.html> 1999. 20 Nov 2002.
[6] Ibid.
[7] Ibid.
[8] S.R. Searle. Matrix Algebra for Business and Economics. (New York: Wiley-Interscience) 1970: 41.
[9] Ibid.
[10] S.R. Searle. Matrix Algebra for Business and Economics. (New York: Wiley-Interscience) 1970: 42.
[11] Ibid, 43.
[12] S.R. Searle. Matrix Algebra for Business and Economics. (New York: Wiley-Interscience) 1970: 43.
[13] Ibid.
[14] Ibid.
Works Cited:
Searle, S.R. Matrix Algebra for Business and Economics. New York: Wiley Interscience, 1970.
Weisstein, Eric. "Linear Transformation". World of Mathematics.
<http://mathworld.wolfram.com/LinearTransformation.html> 1999. 20 Nov
2002.
Yahoo! Reference - The Britannica Concise - linear transformation
<http://education.yahoo.com/search/be?lb=t&p=url%3al%2flinear_transformation > 20 Nov 2002.
 |
|||||||||
| Who is Eric? | Economics | English | Ethics | History | Interests | Leadership | Psychology | Politics | Links |
Date this page was last updated: 12/06/2002
for any
.
